Кинематика

1. По рисункам определить проекции векторов, их длины, графически найти сумму векторов, проекцию суммы векторов, длину суммарного вектора.

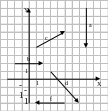
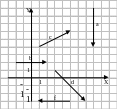
рис.1 рис.2

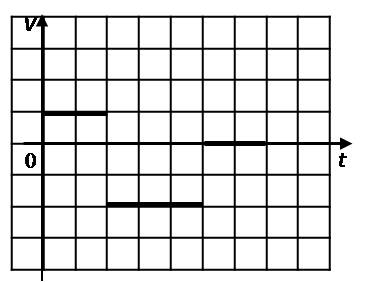2. И спользуя графики зависимости скорости от времени, нарисовать графики зависимости перемещения и координаты от времени.

р ис.3 рис.4

3. Охарактеризовать движение заданное уравнением

1. х = 3 + 4t + 2t²

2. x = 8 – 5t + 9t²

3. x = 2 – 6t – 3t²

4. x = 4t – t²

5. х = 5 + 8t + 4t²

6. x = 6 –t + 3t²

7. x = 2 – 4t – t²

8. x = – 2t²

4. Используя график зависимости скорости от времени найти ускорение тел и записать уравнение движения, если x₀ = 8.

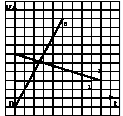
рис.1 рис.2

7. Скорость движения автомо­биля за 40 с возросла от 5 м/с до 15 м/с. Определите ускорение ав­томобиля.

8. Двигаясь со скоростью 72 км/ч, мотоциклист притормо­зил и через 20 с достиг скорости 36 км/ч. С каким ускорением он тормозил?

9. Через сколько секунд после отправления от станции скорость поезда метрополитена достигнет 72 км/ч, если ускорение при разгоне равно 1 м/с²?

7. Какую скорость приобре­тает автомобиль при торможении с ускорением 0,5 м/с² через 10 с от начала торможения, если началь­ная скорость его была равна 36 км/ч?

8. Через сколько времени от начала движения трамвай приобре­тает скорость 10 м/с, если он от­ ходит от остановки с ускорением 0,5 м/с²?

9. При прямолинейном дви­жении с постоянным ускорением 0,2 м/с² велосипедист достигает ско­рости 5 м/с за 25 с. Какова была начальная скорость велосипедиста?

10. Лыжник спускается с горы с начальной скоростью 6 м/с и ускорением 0,5 м/с². Какова длина горы, если спуск с нее продолжался 12 с?

11. Автобус движется со скоростью 54 км/ч. На каком расстоянии от оста­новки водитель должен начать торможение, если для удобства пассажиров ус­корение не должно превышать 1,2 м/с²?

12. Уравнение движения материальной точки имеет вид: x = = —0,2 t². Какое это движение? Найти координату топки через 5 с и путь, пройденный ею за это время.

13. Имея начальную скорость 36 км/ч, троллейбус за 10 с прошел путь: а) 120 м; б) 100 м; в) 80 м. С каким ускорением двигался троллейбус в каждом случае и какие скоростной при­ обретал в конце пути?

14. Уклон длиной 100 м лыжник прошел за 20 с, двигаясь с ускорением 0,3 м/с². Какова скорость лыжника в начале и в конце уклона?

15. Троллейбус двигался со скоростью 18 км/ч и, затормозив, остановил­ся через 4с. Определите ускорение и тормозной путь троллейбуса.

16. При какой скорости самолет может приземлиться на посадочной полосе аэродрома длиной 800 м при торможении с ускорением 5 м/с²?

17. Поезд, отходя от станции, движется с ускорением 0,05 м/с². Сколько времени ему понадобится для достижения скорости 10 м/с и какое расстояние он пройдет за это время?

18. За 3 с от начала движе­ния автомобиль приобрел скорость 9 м/с. Какой путь он прошел при этом?

19. Через сколько времени от начала движения велосипедист про­ ходит путь 20 м при ускорении 0,4 м/с²?

20. Санки скатились с горы длиной 36 м за 60 с. С каким уско­рением двигались санки?

21. При какой начальной ско­рости поезд пройдет путь 3260 м в течение 60 с, замедляя ход с ус­корением 1,5 м/с²?

22. Тормоз легкового автомо­биля исправен, если при скорости движения 8 м/с тормозной путь равен 7,2 м. Каково время тормо­жения и ускорение автомобиля?

23. Самолету для взлета нужно приобрести скорость, равную 252 км/ч. Сколько времени длится разгон, если эта скорость достигается в конце взлет­ной полосы длиной 980 м?

24. За время торможения, равное 5 с, скорость автомобиля уменьшилась с 72 км/ч до 36 км/ч. Определите ускорение автомобиля при торможении и длину тормозного пути.

25. Пуля, летящая со скоростью 400 м/с, влетела в деревянную доску и углубилась в лес на 20 см. С каким ускорением двигалась пуля внутри доски? На какой глубине скорость пули уменьшилась в 2 раза?

7. Поезд, двигаясь под уклон, прошел за 20 с путь 340 м и развил скорость 19 м/с. С каким ускорением двигался поезд и какой была его скорость в начале уклона?

8. Заданы уравнения движения по шоссе различных тел: а) x₁= —0,4 t² — для велосипедиста; б) x₂= —200+16t—l,5f² — для грузового автомобиля; в) x₃=800—0,6t — для пешехода; t) х₄= —150 — для бензовоза. Описать картину движения (из какой точки, в какую сторону, с какой начальной скоростью, с каким ускорением, каким являет­ся движение).

9. Движения материальных точек заданы следующими уравнениями: а) x₁=10t+0,4t²; б)x₂=2t—t2; в) х₃= — 4t+2t²; г) х₄= —t — 6t². Написать зависимость v=v(t) для каждого случая; построить графики этих зависимостей; определить вида движения в каждом случае.

10. Мальчик съехал на санках с горы длиной 40 м за 10с, а затем проехал по горизонтальному участку еще 20 м до останов­ки. Найти скорость в конце горы, ускорения на каждом из уча­стков, общее время движения и среднюю скорость на всем пути. Начертить график скорости.

11. Велосипедист начал свое движение из состояния покоя и в течение первых 4 с двигался с ускорением 1 м/с² затем в течение 0,1 мин он двигался равномерно и последние 20 м — равнозамедленно до остановки. Найти среднюю скорость за все время движения. Построить график v=v(t),

12. Расстояние между двумя станциями поезд прошел со средней скоростью v_ср=72 км/ч за t=20 мин. Разгон и торможе­ние вместе длились t=4 мин, а остальное время поезд двигался равномерно. Какой была скорость v поезда при равномерном движении?

13. Движения двух автомобилей по шоссе заданы уравнения­ ми х₁=2t+0,2t² и х₂^:=80—4t. Описать картину движения; найти время и место встречи автомобилей; расстояние между ними через 5 с; координату первого автомобиля в тот момент време­ни, когда второй находился в начале отсчета.

14. Два автомобиля выезжают из одного пункта в одном направле­нии. Первый автомобиль выезжает на 20с позже другого. Оба движутся с одинаковым ускорением, равным 0,4 м/с². Через сколько времени, считая от начала движения первого автомобиля, расстояние между ними окажет­ся равным 240 м?

7. Два велосипедиста едут навстречу друг другу. Первый, имея скорость 27 км/ч, поднимается в гору с ускорением 0,15 м/с², а второй, имея скорость 9 км/ч, спускается с горы с ускорением 0,25 м/с². Через какой промежуток вре­мени они встретятся, если известно, что встреча произойдет на середине пути?

7. Автобус, отходя от остановки, движется равноускоренно и проходит за третью секунду 2,5 м. Определите путь, пройденный автобусом за пятую секунду.

8. С каким ускорением движется тело, если за шестую секунду этого дви­жения оно прошло путь, равный 11м? Начальная скорость движения равна нулю.

9. Движение двух автомобилей описывается следующими уравнениями: x_t= 2t + 0,2t² и х₂ = 80 - 4t. Определите, когда и где произойдет их встреча. Най­дите расстояние между ними через 5 с после начала движения.

10. Уравнения движения двух тел имеют следующий вид: x₁=10t+0,4t² и x₂=-6t+2t². Найдите место и время их встречи. Каким будет расстояние между ними через 5 с?

11. Мяч брошен вертикально вверх. Как направлены начальная скорость мяча и его ускорение?