4.6. Обработка результатов эксперимента

Запустить в среде Mathcad файл «Снятие характеристик двухэлектродной лампы». Результаты измерений температурной характеристики катода и анодных характеристик лампы ввести в соответствующие поля ввода. Следя за указаниями компьютерной модели, построить график зависимости тока насыщения от напряжения накала , семейство анодных характеристик диода, полученное для разных напряжений накала: , семейство зависимостей сопротивления лампы от анодного напряжения

Используя семейство анодных характеристик, определить с помощью модели внутреннее динамическое сопротивление лампы при разных напряжениях накала.

Проанализировать полученные результаты, сделать выводы.

4.7. Оформление отчета

Отчет должен содержать следующие данные: наименование и цель работы, схему установки; таблицу результатов; графики, определенные с помощью модели значения внутреннего динамического сопротивления лампы при разных напряжениях накала, выводы.

Литература: [1], с. 152 – 154; [3], с. 207 – 214.

Лабораторная работа Э-5

ОПРЕДЕЛЕНИЕ УДЕЛЬНОГО ЗАРЯДА ЭЛЕКТРОНА

5.1. Цель работы

Измерение отношения заряда электрона к его массе методом магнетрона.

5.2. Общие положения

Метод магнетрона относится к числу точных современных методов определения отношения .

Магнетрон простейшей конструкции – это двухэлектродная лампа, содержащая цилиндрический анод и прямолинейный катод, расположенный вдоль оси анода, и помещенная во внешнее магнитное поле.

Подогреваемый током от внешнего источника катод испускает электроны.

Если между электродами лампы в отсутствии магнитного поля приложить разность потенциалов, то электроны, вылетающие с катода, движутся к аноду по радиальным прямым (рис. 5.1а). При этом электроны приобретают кинетическую энергию, равную работе сил электрического поля

Отсюда следует, что скорость, приобретаемая электроном,

, (5.1)

При этом в анодной цепи течет ток.

Если создать магнитное поле, направленное вдоль оси катода, то на движущиеся электроны будет действовать сила Лоренца , перпендикулярная скорости движения электрона, которая будет искривлять траекторию движения электрона (см. рис. 5.1б).

Чем больше значение индукции магнитного поля, тем меньше величина радиуса кривизны траектории электрона. При некотором значении индукции магнитного поля траектории искривляются так, что только касаются поверхности анода, являются замкнутыми кривыми. При дальнейшем увеличении поля, радиус кривизны уменьшается настолько, что электроны, не долетая до анода, поворачивают о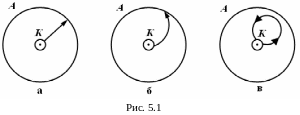 братно и возвращаются на катод (рис. 5.1в). Анодный ток в лампе при этом прекращается.

Таким образом, с помощью магнитного поля можно управлять анодным током в электронной лампе.

В настоящей работе магнитное поле создается током , текущим через соленоид. Соленоид надевают на баллон электронной лампы так, чтобы направление поля совпало с осью, вдоль которой расположен катод.

Будем считать, что траектория электрона – окружность радиуса , где – радиус анода. Сила Лоренца является центростремительной, вызывающей вращение электрона, поэтому можно записать