2.3. Описание лабораторной установки

Сущность метода компенсации состоит в следующем. Нормальный элемент Вестона и неизвестный, ЭДС которого определяют, соединяют одинаковыми полюсами навстречу друг другу, как показано на рис. 2.1. Здесь является исследуемым элементом, т.е. неизвестной ЭДС. Он замкнут на известное сопротивление, составляющее два участка цепи: и . Нормальный элемент соединен последовательно с гальванометром и сопротивлением (от 1·10⁴ до 2·10⁴ Ом), которое ограничивает силу тока в цепи нормального элемента.

Е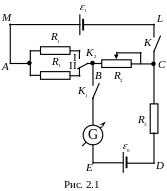 сли ЭДС больше ЭДС то сопротивление участков цепи и можно подобрать так, чтобы падение напряжения на участке было равно ЭДС нормального элемента. При этом гальванометр , включенный в цепь нормального элемента, покажет нуль тока. Следовательно, ЭДС нормального элемента будет скомпенсирована разностью потенциалов на участке . Это вытекает из уравнения Кирхгофа.

Рассмотрим это более подробно. Обозначим (см. рис. 2.1) сопротивление участка цепи через , ток на этом участке – через , сопротивление участка цепи – через , ток на этом участке – , ток, проходящий через нормальный элемент, – , сопротивление подводящих проводов и внутреннее сопротивление нормального элемента – .

Если применить второе правило Кирхгофа к контуру , то получим уравнение

. (2.3)

Из этого уравнения видно, что если – ток в цепи нормального элемента, измеряемый гальванометром, равен нулю, то , то есть падение напряжения на участке цепи компенсируется – ЭДС нормального элемента. Ток найдем, применив второе правило Кирхгофа к контуру , т.е.

, (2.4)

где – внутреннее сопротивление элемента и сопротивление подводящих проводов. Но из первого правила Кирхгофа следует, что в точке цепи сумма токов ; причем, если , то . Следовательно, .

Отсюда . Подставим значение в формулу и получим

,

или . (2.5)

Из соотношения (2.5) можно определить при условии, что известно. Но – неизвестно, исключим его, получив еще одно подобное равенство.

Для этого изменим величину сопротивления участка на . При этом в гальванометре потечет ток – компенсация нарушается. Подобрав соответствующее сопротивление , можно снова скомпенсировать ЭДС нормального элемента и получить падение напряжения на участке , равное , и ток, проходящий через гальванометр, равный нулю.

Для этих условий уравнение (2.5) будет иметь вид:

.

Вычитая это выражение из уравнения (2.5), получим

.

Отсюда

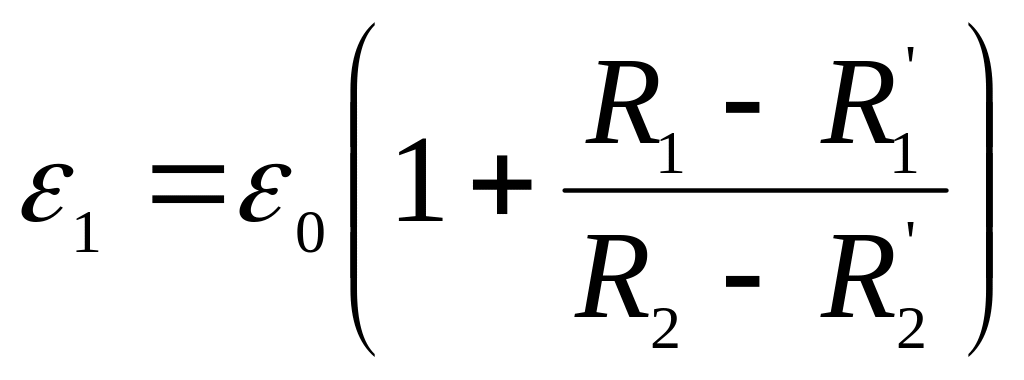. (2.6)

Из этого уравнения можно определить ЭДС искомого элемента , если известны ЭДС нормального элемента и сопротивления , , , . Получив значение ЭДС , из уравнения (2.5) можно определить и внутреннее сопротивление искомого элемента .

Точность компенсации зависит от чувствительности гальванометра, однако класс точности прибора здесь не играет роли, так как гальванометр не измеряет ток, а только показывает его наличие.

Для выполнения работы необходимо: два источника постоянного тока (один из них с неизвестной ЭДС, а другой – элемент Вестона); гальванометр, класс точности не хуже 1,0; магазин сопротивлений; несколько (3 шт.) резисторов.

На макете собрана схема согласно рис 2.1. Перед выполнением работы тщательно изучить макет, понять способ набора резисторов на магазине сопротивлений .