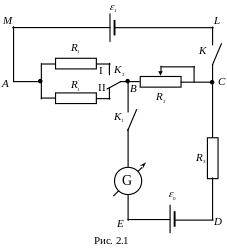
2.3. Опис лабораторної установки

Суть методу компенсації полягає в наступному. Нормальний елемент Вестона і невідомий, ЕРС якого визначають, сполучають однаковими полюсами назустріч один одному, як показано на рис. 2.1. Тут є досліджуваним елементом, тобто невідомою ЕРС. Він замкнутий на відомий опір, що утворює дві ділянки кола: і . Нормальний елемент сполучений послідовно з гальванометром і опором (від 1·10⁴ до 2·10⁴ Ом), який обмежує силу струму в колі нормального елементу.

Якщо ЕРС більше ЕРС то опір ділянок кола і можна підібрати так, щоб спад напруги на ділянці був рівним ЕРС нормального елементу. При цьому гальванометр, включений в коло нормального елементу, покаже нуль струму. Отже, ЕРС нормального елементу компенсуватиметься різницею потенціалів на ділянці . Це витікає з рівняння Кірхгофа.

Розглянемо це детальніше. Позначимо (див. Рис. 2.1) опір ділянки кола через , струм на цій ділянці – через , опір ділянки кола – через , струм на цій ділянці – , струм, що проходить через нормальний елемент, – , опір підвідних проводів і внутрішній опір нормального елементу – .

Якщо застосувати друге правило Кірхгофа до контуру , то отримаємо рівняння

. (2.3)

З цього рівняння видно, що якщо – струм в колі нормального елементу, вимірюваний гальванометром, дорівнює нулю, то , тобто спад напруги на ділянці кола компенсується – ЕРС нормального елементу. Струм знайдемо, застосувавши друге правило Кірхгофа до контуру , тобто

, (2.4)

де – внутрішній опір елементу і опір підвідних проводів. Але з першого правила Кірхгофа виходить, що в точці кола сума струмів ; причому, якщо , то . Отже

.

Звідси . Підставимо значення у формулу і отримаємо

,

або . (2.5)

Із співвідношення (2.5) можна визначити за умови, що відомий. Але – невідомий, виключимо його, отримавши ще одну подібну рівність.

Для цього змінимо величину опору ділянки на . При цьому в гальванометрі потече струм – компенсація порушується. Підібравши відповідний опір , можна знову компенсувати ЕРС нормального елементу і отримати спад напруги на ділянці , рівний , і струм, що проходить через гальванометр, рівний нулю.

Для цих умов рівняння (2.5) матиме вигляд:

.

Віднімаючи цей вираз з рівняння (4.5), отримаємо

.

Звідси

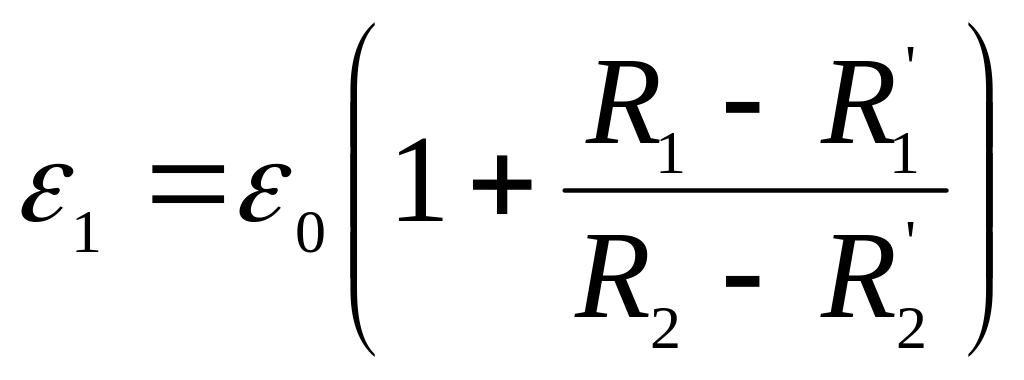. (2.6)

З цього рівняння можна визначити ЕРС шуканого елементу , якщо відомі ЕРС нормального елементу і опори , , , . Отримавши значення ЕРС , з рівняння (2.5) можна визначити і внутрішній опір шуканого елементу .

Точність компенсації залежить від чутливості гальванометра, проте клас точності приладу тут не грає ролі, оскільки гальванометр не вимірює струм, а лише показує його наявність.

Для виконання роботи необхідні: два джерела постійного струму (один з них з невідомою ЕРС, а інший – елемент Вестона); гальванометр, клас точності не гірше 1,0; магазин опорів; декілька (3 шт.) резисторів.

На макеті зібрана схема згідно рис. 2.1. Перед виконанням роботи ретельно вивчити макет, зрозуміти спосіб набору резисторів на магазині опорів .