Литература: [1] с. 143 - 158, 513 - 519; [2] с. 133 - 161; [3] с. 90 - 96

Лекция № 7. Основы химической термодинамики. Термохимические расчеты

Химическая термодинамика – это раздел физической химии, изучающий энергетические эффекты и направленность химических процессов. Предметом изучения термодинамики является термодинамическая система - тело или совокупность тел в объеме, ограниченном от окружающей среды реальными или условными перегородками. Выделяют три типа термодинамических систем:

• изолированные, которые не обмениваются с окружающей средой ни массой, ни энергией;

• закрытые, которые обмениваются с окружающей средой энергией, но не обмениваются массой;

• открытые, для которых возможен свободный массо- и энергообмен с окружающей средой.

По фазовому составу различают гомогенные и гетерогенные системы. Гомогенные системы состоят из одной фазы, гетерогенные включают несколько фаз. Фаза - это совокупность однородных частей системы, обладающих одинаковыми свойствами во всех ее точках, ограниченная от других частей системы поверхностью раздела.

Состояние системы описывается рядом параметров: химическим составом, температурой, давлением, объемом, массой, количеством вещества. Кроме этого для описания системы и происходящих в ней изменений (термодинамических процессов) применяется ряд термодинамических функций: внутренняя энергия, энтальпия, энтропия, изобарно-изотермический потенциал (свободная энергия Гиббса).

Внутренняя энергия (U) - это совокупность всех видов энергии термодинамической системы за исключением кинетической энергии ее движения как целого и потенциальной энергии ее положения в каком-либо внешнем поле. Поскольку во внутреннюю энергию входят все виды энергии, заключенные в материи, даже те, которые нам еще неизвестны, абсолютное ее значение не подлежит определению. Тем не менее, можно определить изменение внутренней энергии в результате какого-либо процесса (U = U₂ - U₁). При этом величина изменения внутренней энергии не зависит от пути проведения процесса, а определяется только конечным и начальным состоянием системы, т.е. внутренняя энергия является функцией состояния:

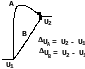
В термодинамике различают два вида процессов: изохорный, проводимый при постоянном объеме, и изобарный, проводимый при постоянном давлении. Тепло, сообщенное системе в изохорном процессе, идет на увеличение ее внутренней энергии: Q_V = U.

Тепло, сообщенное системе в изобарном процессе, идет на увеличение ее внутренней энергии и совершение работы против сил внешнего воздействия: Q_p = U + A. Последнее выражение представляет собой одну из формулировок первого начала термодинамики. Поскольку при сообщении тепла при постоянном давлении система расширяется, она совершает работу против силы внешнего давления: A = pV. Подставим эту формулу в математическое выражение первого начала термодинамики и сгруппируем переменные:

Q_p = U + pV = U₂ - U₁ + p(V₂ - V₁) = (U₂ + pV₂) - (U₁ + pV₁) = H₂ - H₁ = H

Из полученного выражения следует, что тепло, сообщенное системе при изобарном процессе, идет на увеличение функции H = U + pV. Эта функция получила название - энтальпия. Следует отметить, что, так же как и внутренняя энергия, энтальпия является функцией состояния и ее изменение не зависит от пути проведения процесса, а определяется конечным и начальным состоянием системы. Поскольку в выражение энтальпии входит внутренняя энергия, абсолютное ее значение также неопределимо.

Энтальпия широко используется в термохимических расчетах, целью которых является определение теплового эффекта химической реакции, проводимой обычно при постоянном давлении. Выполняются расчеты на основании термохимических уравнений, которые заметно отличаются от химических уравнений реакций. Например, термохимическое уравнение реакции образования воды будет выглядеть следующим образом:

H₂(г) + 1/2O₂(г) = H₂O(ж); H₂₉₈ = -285,83 кДж

Отличия от обычного уравнения химической реакции (2H₂ + O₂ = 2H₂О) заключаются в следующем:

• Коэффициенты в термохимическом уравнении указывают на количество вещества, поэтому могут быть дробными и обычно подбираются таким образом, чтобы целевой продукт реакции имел коэффициент, равный единице.

• Указывается тепловой эффект в виде изменения энтальпии (H). Следует обратить внимание на то, что процесс рассматривается со стороны термодинамической системы, поэтому для экзотермических реакций H имеет отрицательное значение, а для эндотермических - положительное.

• Обязательно указывается агрегатное состояние реагентов и продуктов реакции, поскольку изменение агрегатного состояния (фазовый переход) требует энергетических затрат и влечет за собой изменение теплового эффекта, например,

H₂(г) + 1/2O₂(г) = H₂O(ж); H₂₉₈ = -285,83 кДж

H₂(г) + 1/2O₂(г) = H₂O(г); H₂₉₈ = -241,82 кДж

Одной из фундаментальных термодинамических характеристик вещества является стандартная энтальпия образования (H⁰_f) - изменение энтальпии в процессе образования одного моля вещества из простых веществ в стандартных условиях. Стандартному состоянию в термодинамике отвечает температура 298 К (25 С) и давление 101,325 кПа (1 атм.). Из определения следует, что энтальпия образования простого вещества, наиболее устойчивого в стандартных условиях, равна нулю. Найти величины стандартных энтальпий образования многих веществ можно в соответствующих справочниках.

В основе термохимических расчетов лежит закон Гесса (Г.И. Гесс, 1841) - тепловой эффект химической реакции не зависит от пути проведения процесса и числа его промежуточных стадий, а определяется начальным и конечным состоянием системы. Конкретные расчеты выполняют на основании следствий из закона Гесса.

Следствие первое - с термохимическими реакциями можно выполнять арифметические операции. Таким образом, комбинируя термохимические уравнения, можно определять тепловые эффекты в принципе любых реакций, в том числе и тех, для которых его определение связано с экспериментальными сложностями или вообще невыполнимо. Например, невозможно экспериментально определить тепловой эффект реакции образования оксида углерода(II):

С(графит) + 1/2О₂(г) = СО(г),

поскольку большое сродство углерода к кислороду приводит к образованию примеси СО₂ даже при недостатке кислорода. В то же время легко поддаются экспериментальному определению тепловые эффекты следующих реакций:

С(графит) + О₂(г) = СО₂(г); H₁ = -393,5 кДж

СO(г) + 1/2O₂(г) = CO₂(г); H₂ = -283 кДж

Вычтя второе уравнение из первого, получим уравнение образования оксида углерода(II):

С(графит) + О₂(г) - СO(г) + 1/2O₂(г) = СО₂(г) - СО₂(г)

С(графит) - СO(г) + 1/2O₂(г) = 0

С(графит) + 1/2O₂(г) = СO(г)

Соответствующая комбинация тепловых эффектов реакций дает искомый тепловой эффект

H = H₁ - H₂ = -393,5 - (-283) = -110,5 (кДж)

Следствие второе - тепловой эффект химической реакции равен разности суммы энтальпий образования продуктов реакции и суммы энтальпий образования исходных веществ (реагентов).

H⁰₂₉₈ = iH⁰_f(пр) - jH⁰_f(реаг)

Применение данного следствия позволяет рассчитать тепловой эффект любой реакции, для которой известны стандартные энтальпии образования реагентов и продуктов реакции (справочные данные).

Рассчитаем в качестве примера тепловой эффект реакции термического разложения карбоната кальция:

CaCO₃(к) = CaO(к) + CO₂(г)

H⁰₂₉₈ = H⁰_f(CaO) + H⁰_f(CO₂) - H⁰_f(CaCO₃)

H⁰₂₉₈ = -635,5 + (-393,5) - (-1206,9) = 177,9 кДж

Следствие третье - тепловой эффект химической реакции равен разности суммы энтальпий сгорания исходных веществ и суммы энтальпий сгорания продуктов реакции.

H⁰₂₉₈ = iH⁰_сгор(реаг) - jH⁰_сгор(пр)

В качестве примера рассчитаем энтальпию процесса перехода цис-бутена-2 в транс-изомер.

cis-С₄Н₈ = trans-C₄H₈

H⁰₂₉₈ = H⁰_сгор(cis-C₄H₈) - H⁰_сгор(trans-C₄H₈); H⁰₂₉₈ = -2710,4 - (-2706,2) = -4,2 кДж

В основе химических процессов, наряду со стремлением к минимуму энергии, отчетливо проявляется тенденция системы к переходу в состояние с максимальной неупорядоченностью расположения частиц. Для отражения этой тенденции в термодинамике существует специальная функция - энтропия (S), которая определяется уравнением Больцмана:

S = RlnW,

где W - термодинамическая вероятность системы.

Термодинамической вероятностью называется число микросостояний системы (способов расположения ее частиц), отвечающее данному ее макросостоянию. Рассмотрим в качестве модельной системы, распределение четырех молекул газа по двум половинам сосуда.

W = 1 W = 4 W = 6 W = 4 W = 1

Первое состояние можно реализовать только одним способом. Второе состояние можно реализовать четырьмя способами, меняя молекулу в левой части системы. При реализации третьего состояния возможны шесть перестановок молекул, поэтому вероятность данного состояния равна шести. Очевидно, что термодинамическая вероятность, а соответственно и энтропия состояния, отвечающего равномерному распределению молекул в системе максимальна. Стремление системы перейти в состояние с максимальной неупорядоченностью отражает второе начало термодинамики - процессы, не сопровождающиеся энергетическими эффектами, самопроизвольно идут в сторону увеличения энтропии.

Следует отметить, что, в отличие от внутренней энергии и энтальпии, энтропия может быть рассчитана методами статистической термодинамики. Изменение энтропии в результате какого-либо процесса можно рассчитать по второму следствию закона Гесса, поскольку энтропия является функцией состояния системы. Можно определить изменение энтропии и экспериментально, зная количественно тепла, переданного в изотермическом процессе:

,

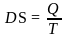где Q - теплота, которой система обменивается с внешней средой при постоянной температуре Т.

Как уже отмечалось, в основе химических реакций лежат две противоположно направленные тенденции:

• стремление частиц к соединению с образованием химических связей и выделением энергии;

• стремление атомов к разрыву химических связей и увеличению энтропии.

Попытаемся определить, какая из тенденций будет превалировать в тех или иных условиях. Для этого перепишем уравнение первого начала термодинамики, разделив работу на работу расширения - pV и полезную работу - А_пол

U = Q_p - A_пол - pV

Поскольку H = U + pV, а U = H - pV данное уравнение можно преобразовать к следующему виду:

H = Q - A_пол

Так как S = Q/T, а Q = TS, то

H = ТS - A_пол

A_пол = -(H - ТS)

Это значит, что в системе может совершаться работа химического процесса, т.е. он может идти самопроизвольно, только в том случае, когда H - ТS < 0. Комбинация термодинамических функций сама является функцией состояния, которая получила название свободная энергия Гиббса (G) или изобарно-изотермический потенциал G = H - ТS.

Величина изменения свободной энергии Гиббса позволяет решить вопрос о принципиальной возможности химической реакции:

G < 0 - реакция принципиально осуществима;

G > 0 - реакция принципиально не осуществима;

G = 0 - система находится в состоянии химического равновесия.

Аналогично энтальпии образования в термодинамике широко используется энергия Гиббса образования (G_f⁰), как изменение свободной энергии Гиббса в процессе образования одного моля вещества из простых веществ в стандартных условиях. Энергии Гиббса образования - табличные величины, на основании которых по закону Гесса можно рассчитать G для той или иной реакции:

G⁰₂₉₈ = iG_f⁰(пр) - jG_f⁰(реаг)