Комплексні креслення групи геометричних тіл і моделей

Для розвитку просторової уяви корисно виконувати комплексні креслення групи геометричних тіл і нескладних моделей з натури.

Малюнок 22

Наочне зображення групи геометричних тіл показане на мал. 22, а. Побудову комплексного креслення цієї групи геометричних тіл слід розпочинати з горизонтальної проекції, оскільки основи циліндра, конуса і шестигранної піраміди проектуються на горизонтальну площину проекції без спотворень. За допомогою вертикальних ліній зв'язку будують фронтальну проекцію. Профільну проекцію будують за допомогою вертикальних і горизонтальних ліній зв'язку(мал. 22, б).

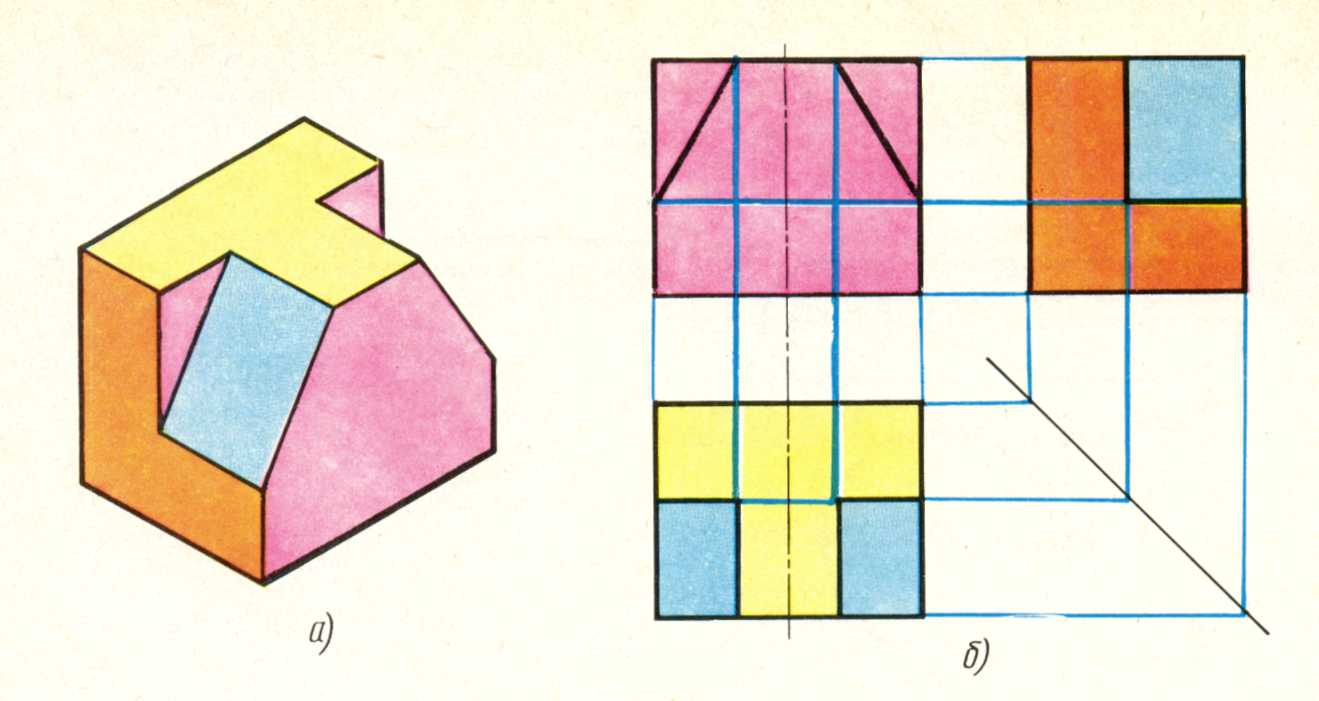
Малюнок 23

Щоб перейти до складніших моделей, необхідно засвоїти побудову простих комплексних креслень. Проекції моделей слід розташовувати так, щоб фронтальна проекція давала на повне уявлення про форму і розміри i(мал. 23).

Поняття про перерізи геометричних тіл

Деталі машин і приладів дуже часто мають форми, що є різними геометричними поверхнями, розітнутими площинами(мал. 24). Завдання побудови проекцій таких перерізів нерідко зустрічаються при виконанні креслень деталей машин і приладів. Крім того, іноді необхідно виконати розгортки поверхні порожнистих деталей, усічених площиною. Це застосовується в розкрої листового матеріалу, з якого виготовляються порожнисті деталі.

Такі деталі зазвичай є частині всіляких трубопроводів,вентиляційних пристроїв, кожухів для закриття механізмів, обгороджування верстатів і т. п.(мал. 24 і 25).

Побудови прямокутних і аксонометричних проекцій усічених тіл, а також визначення істинного виду перерізів і розгорток поверхонь геометричних тіл сприяють засвоєнню основ проекційного креслення. Розтинаючи геометричне тіло площиною, отримують переріз – плоску фігуру, обмежену лінією, усі точки якої належать як січній площині, так і поверхні тіла.

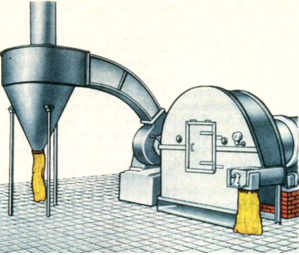
Малюнок 24

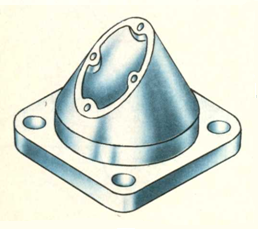
Малюнок 25

При перетині площиною многогранника(наприклад,призми, піраміди) в перерізі виходить багатокутник з вершинами, розташованими на ребрах многогранника. При перетині площиною тіл обертання(наприклад,циліндра, конуса) фігура перерізу часто обмежена кривою лінією. Точки цієї кривої знаходять за допомогою допоміжних ліній - прямих або кіл, узятих на поверхні тіла. Точки перетину цих ліній з січною площиною будуть шуканими точками контура криволінійного перерізу.

Приклад перерізу площиною Р геометричного тіла - куба,що лежить на горизонтальній площині проекції Н,показаний на мал. 26.

У першому випадку(мал. 26, а) куб усічений фронтально - проектуючий площиною Р. Фігурою перерізу є прямокутник.

При побудові двох проекцій такого перерізу(мал. 26, б)слід мати на увазі, що фронтальна проекція фігури перерізу співпадає з фронтальним слідом січної площини Pv.

Горизонтальна проекція фігури перерізу - прямокутник.

У другому випадку(мал. 26, в) куб усічений горизонтально - проектуючою площиною Р. Фігура перерізу - прямокутник.

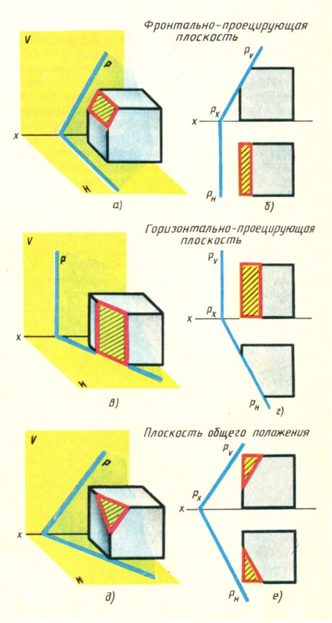
Малюнок 26

На мал. 26, г приведена побудова проекцій цього перерізу. Горизонтальна проекція фігури перерізу співпадає з горизонтальним слідом Рн січної площини. Фронтальною проекцією перерізу буде прямокутник,однією стороною якого є лінія перетину площини Р з площиною передньої грані куба.

Якщо куб пересічений площиною загального стану(мал. 26, д), то отримана фігура перерізу в даному випадку(трикутник) проектується на площини проекцій V і Н із спотворенням.