Малюнок 15

Визначення недостатніх проекцій точок А до В,розташованих на поверхні циліндра, по заданих фронтальних проекціях в даному випадку утруднень не викликає, оскільки уся горизонтальна проекція бічної поверхні циліндра є колом(мал. 15, а). Отже,горизонтальні проекції точок А я В можна знайти,проводячи з цих точок а' і b' вертикальні лінії зв'язку до їх перетину з колом в шуканих точках a і b.

Профільні проекції точок А і У будують також за допомогою вертикальних і горизонтальних ліній зв'язку.

Ізометричну проекцію циліндра викреслюють, як показано на мал. 15, би.

У ізометрії точки А до У будують по їх координатах. Наприклад, для побудови точки У від початку координат 0 по осі х відкладають координату хв=п, а потім через її кінець проводять пряму, паралельну осі у, до перетину з контуром основи в точці 1. З цієї точки паралельно осі z проводять пряму, на якій відкладають координату zB, - h1точки В

Проекції косинусів

Наочне зображення прямого кругового конуса показане на мал. 16, а. Бічна поверхня конуса виходить при обертанні відрізку BS навколо осі конуса по тій, що направляє - кола основи. Послідовність побудови двох проекцій конуса показана на мал. 16, б'ючи. Спочатку будують дві проекції основи. Горизонтальна проекція основи - коло. Фронтальною проекцією буде відрізок горизонтальної прямої, рівний діаметру цього кола(мал. 16, б). На фронтальній проекції з середини основи настроюють перпендикуляр і на нім відкладають висоту конуса(мал. 16, в). Отриману фронтальну проекцію вершини конуса сполучають прямими з кінцями фронтальної проекції основи і отримують фронтальну проекцію конуса.

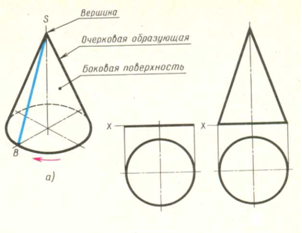
Малюнок 16

Якщо на поверхні конуса задана одна проекція точки А,те дві інші проекції цієї точки визначають за допомогою допоміжних ліній - що утворює, розташованою на поверхні конуса і проведеною через точку А, або колу,розташованому в площині, паралельній основі конуса.

У першому випадку(мал. 17, а) проводять фронтальну проекцію s'a'f такою, що допоміжною, що утворює. Користуючись вертикальною лінією зв'язку, проведеного з точки /, розташованого на фронтальній проекції кола основи, знаходять горизонтальну проекцію sf такою, що цією, що утворює, на якій за допомогою лінії зв'язку, що проходить через а, знаходять шукану точку а.

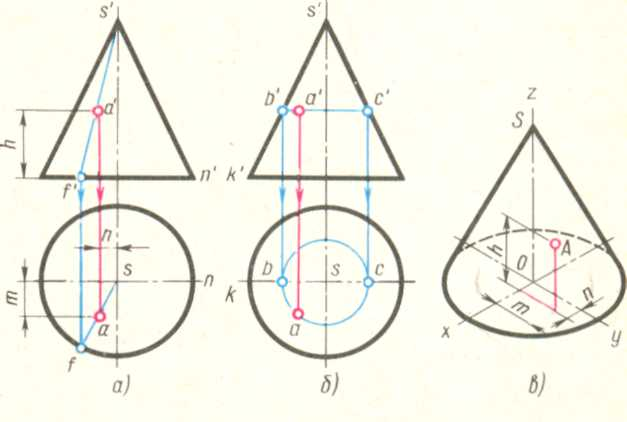
Малюнок 17

У другому випадку(мал. 17, б) допоміжною лінією, що проходить через точку А, буде коло, розташоване на конічній поверхні і паралельне площині Н. Фронтальна проекція цього кола зображається у вигляді відрізку Ъ'с' горизонтальної прямої, величина якого дорівнює діаметру допоміжного кола. Шукана горизонтальна проекція а точки А знаходиться на перетині лінії зв'язку,опущеного з точки а, з горизонтальною проекцією допоміжної окружності.

Якщо задана фронтальна проекція Ъ' точки В розташована на контурній(нарисовою) SK, що утворює, то горизонтальна проекція точки знаходиться без допоміжних ліній.

У ізометричній проекції точку А, що знаходиться на поверхні конуса, будують по трьох координатах(мал. 17, в) : xA=N, уА=М і zA=H. Ці координати послідовно відкладають по напрямах, паралельних ізометричних осях. У даному прикладі від точки Про по осі х відкладена координата хА=п; з кінця її паралельно осі у проведена пряма, на якій відкладена координата уА=т; з кінця відрізку, рівного т, паралельно осі z проведена пряма, на якій відкладена координата zA=h. В результаті побудов отримаємо шукану точку А.