3 Определение дополнительных изгибающих моментов и перерезывающих сил при движении судна на волнении

3.1 Расчет эксплуатационного волнового изгибающего момента

Расчет волновых изгибающих моментов выполняется с помощью следующих за­висимостей согласно [1]:

, кН

где h₁– расчетная высота волны определяем по формуле:

_;

,

= 0,93.

С_w =

С_w =

м.

Для судов с ограничением IIСП h₁ уменьшается пропорционально коэффициенту m₁:

_;

_{Тогда расчётная высота волны определится:}

_{h1 = 7,57×0,59 = 4,43 м.}

)– коэффициент статической постановки судна на волну;

= (0,6×a-0,17);

a=0,933 – коэффициент полноты действующей ватерлинии;

= 0,6×0,933-0,17 = 0,39.

c₀ – гидродинамический поправочный коэффициент, зависящий от соотношений T/L и B/L:

B=13,2 м - ширина судна;

T=3,15 м - осадка судна в расчетном случае;

c₁ – поправочный коэффициент, учитывающий влияние скорости судна на волнении (Fr^в) и из­гибающего момента на тихой воде:

c₁ = ,

Fr₁^в -соответствует реально возможной скорости судна на встречном волнении, соответст­вующему эксплуатационной нагрузке [1] :

F r₁^в =

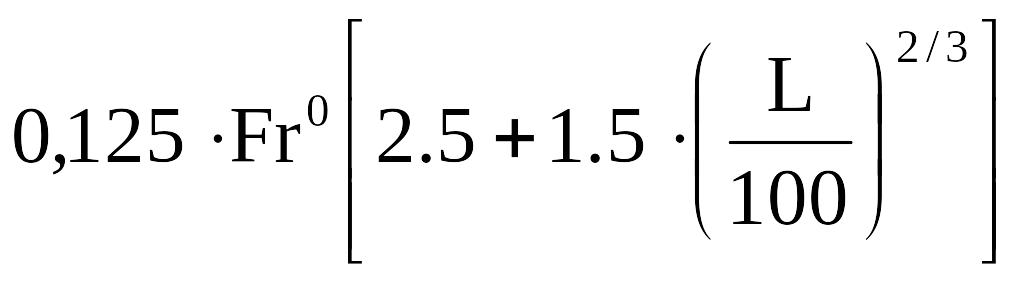
Fr0- число Фруда при движении на тихой воде:

,

V=12,5 узл - скорость движения судна на тихой воде;

g=9,81 м/с2 - ускорение свободного падения;

Fr₁^в = = 0,1.

Число Фруда при движении на волнении не должно превышать значения :

где

,

при =0,933>0,9 принимаем =0,9

Так как Fr₁^в =0,1< =0,19, принимаем Fr₁^в =0,1.

М_тв = 28506,64 кНм – максимальное значение изгибающего момента на тихой воде;

D = 3701,3 т – водоизмещение судна в балласте (табл. 3.3);

c₁ =

Для учёта изменения волнового изгибающего момента по длине судна вводим коэффициент j_м^в(х ) [1] рис 2.1.2-3: для х/L = 0,4 j_м^в = 1

Тогда расчётный изгибающий момент определится:

кНм.

3.2 Расчет ударных изгибающих моментов

Расчет ударного момента для случая удара в днище производится по формуле со­гласно [1]:

М_у^д =

где h_p =0,75 - расчётная высота волны,

h₂ – высота волны для нагрузки обеспеченности Q=

h_{2 = ;}

,

= 1,37;

h₂ = = 10,37 м.

Для судов с ограничением района плавания IIСП h₂ уменьшается пропорционально коэф­фициенту m₂ :

m₂ = ;

m₂ = = 0,67;

h₂ = h₂×m₂

h₂ = 10,37×0,67 = 6,98 м.

Тогда расчётная высота волна :

h_p =0,75×6,98 = 5,23 м.

- параметр относительных перемещений носовой оконечности в районе второго теоретического шпангоута ,

=

= 0,836 – коэффициент общей полноты судна;

= = 0,67;

Принимаем = 0,85

Fr₂^в – соответствует реально возможной скорости судна на встречном волнении, соответствующем предельной нагрузке:

Fr₂^в =

Fr₂^в = = 0,064.

r_м =0,26 – относительная (отнесенная к длине L) величина продольного радиуса инерции масс судна при расчетном водоизмещении;

= 1,21.

Т_н = 2,35 м – осадка носовой оконечности, определяемая по 2^му теоретическому шпангоуту (см. рис.2);

-относительная ширина 2-го теоретического шпангоута при осадке Т=0,1В=1,32 м;

,

b₂ =9,6 м– ширина второго теоретического шпангоута при его осадке Т=0,1В,

b₂ = 0,8 – коэффициент полноты этого шпангоута при указанной осадке;

К_д(t_y) – коэффициент динамичности, определяем в зависимости от параметра t_y по рис.2.1.3- 2 [1].

;

;

-частота упругих колебаний корпуса первого тона. Определяем по формуле:

, рад/с

м⁴-момент инерции миделевого сечения корпуса относительно нейтральной оси,.

К = 3,5 – для сухогрузов

;

;

.

К_д( ) = 1,5;

j_м^д – учитывает изменение изгибающего момента по длине: при х/L=0,4 получаем j_м^д = 1.

х х кНм.

Производим расчет ударного момента для случая удара в борта по формуле:

где =6,1 м высота надводного борта в районе 2-го теоретического шпангоута;

=5,23 м;

;

=1 при x/L=0,4.

Тогда ударный момент:

так как под корнем отрицательное число.