2.3. Построение диаграммы кинетической энергии второй группы звеньев

Для построения этого графика определим кинетическую энергию второй группы звеньев во всех положениях механизма. Кинетическая энергия находиться с достаточной точностью для инженерных расчетов по формуле:

.

Определим кинетическую энергию 2-ой группы звеньев для каждого положения механизма (на примере 4-го положения):

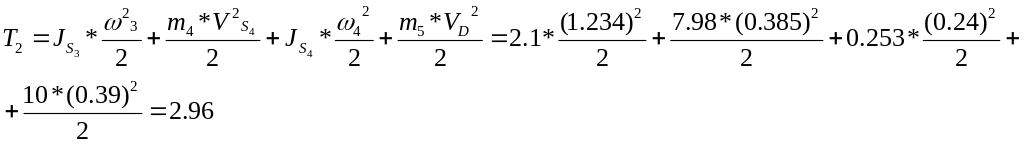
Значения приведённых моментов инерции и кинетических энергий 2-ой группы звеньев представлены в табл.2.3. Строим диаграмму кинетической энергии второй группы звеньев в масштабе :

.

Кинетическая энергия 2-ой группы звеньев
Таблица 2.3
Положение
0	0	0	0	0	0
1	0,41	0,16	0,0015	0,1805	0,752
2	1,164	0,435	0,002	0,528	2,13
3	1,576	0,64	0,00081	0,8	3,02
4	1,6	0,59	0,0073	0,761	2,96
5	1,18	0,49	0,003	0,578	2,25
6	0,273	0,102	0,0025	0,15	0,52
7	0	0	0	0	0
8	1,016	0,409	0,0056	0,481	1,91
9	2,803	1,342	0,0041	1,682	5,83
10	3,45	1,39	0,002	1,682	6,524
11	1,05	0,41	0,003	0,45	1,91
12	0	0	0	0	0

2.4. Построение диаграммы приращения кинетической энергии 1-ой группы звеньев

Диаграмма строится путём вычитания из диаграммы диаграммы . Значения кинетической энергии 1-ой группы звеньев находятся в табл.2.3.1.

Таблица 2.3.1

Положение	0	1	2	3	4	5	6	7	8
,Дж	0	14,04	-15,6	-74,88	-137,28	-193,44	-224,64	-199,68	-156
	0	0,752	2,13	3,02	2,96	2,25	0,52	0	1,91
	0	13,29	-17,72	-77,91	-140,24	-195,69	-225,17	-199,58	-157,9

Положение	9	10	11	12
,Дж	-102,96	-74,88	-37,44	0
	5,83	6,524	1,91	0
	-108,79	-81,4	-39,34	0

Масштабный коэффициент диаграммы равен:

.

Соединив точки плавной кривой, получим искомый график. Максимум и минимум кривой можно определить графически, для чего необходимо провести горизонтальные касательные к графику в точках наибольшего максимума и наименьшего минимума. Расстояние между ними определить в масштабе наибольшее изменение кинетической энергии 1-ой группы звеньев, которое равно:

.

Приведённый момент инерции 1-ой группы звеньев определиться по следующеё формуле:

.

Момент инерции маховика равен:

,

где - момент инерции вращающихся деталей (ротора электродвигателя, редуктора, зубчатых передач), приведённый к кривошипу.

Обычно маховик выполняют в идее массивного кольца, связанного со ступицей с помощью спиц. Если пренебречь моментом инерции спиц и ступицы, то:

,

где m – масса обода колеса, кг;

- средний диаметр обода колеса, м.

Чтобы определить размеры сечения обода b и h, выражают массу обода маховика через его объём:

,

где b- ширина обода, м;

h- толщина обода, м;

p - плотность чугуна, 7800 .

Для определения можно выразить b и h через . Приняв отношение:

; ,- получим:

,

Масса маховика определиться: