4. Описание решения второй задачи

1) Рассчитаем сопротивления всех реактивных элементов в схеме.

X_C1 = = = 29.7619 Ом

X_C2 = = = 52,083 Ом

X_C3 = = = 138,88 Ом

X_L1 =

X_L2 =

X_L3 =

Z₁ = r₁ + j (X_L1-X_С1-X_C2) = 320 + j*(312-29,7619-52,083) = 320 + j* 230,1551

Z₂ = r₂ + j (X _L2) = 290 + j*192

Z₃ = r₃ + j (X_L3-X_C3) = 350 + j*(372-138,88) = 350 + j* 233,12

Алгебраическая форма записи комплексного сопротивления ветви с источником переменного напряжения:

Z₁ = 320 + j* 230,1551

Для того что бы записать его в экспоненциальной форме мы должны найти его модуль и аргумент.

Ом

Arg(Z₁) = arctg =35.7249⁰

Получаем все необходимое для записи в экспоненциальной форме записи:

Z₃ = 394,17175

2) С помощью компьютерного моделирования в программе Multisim определить модуль комплексного сопротивления ветви с источником переменного напряжения. Полученное значение сравнить с пунктом 1. Сделать выводы.

Рис. 4.1 – Данные полученные в результате математического моделирования.

Что бы найти модуль комплексного сопротивления мы должны разность потенциалов поделить на ток в данной цепи.

Z = U/I = 128,762/0.327 = 393,76758 Ом

Данное значение приблизительно совпадает со значением, полученным в расчетах.

Следовательно, расчеты были верны, и комплексное сопротивление найдено правильно.

3) Зададим направления тока в ветвях.

Направление обхода контура примем как по часовой стрелке

Рис. 4.2. Схема с заданными направлениями тока.

Составим уравнения по закону Кирхгофа. Решение уравнений выполняем в программе MathCad. Решение системы уравнений приведено ниже:

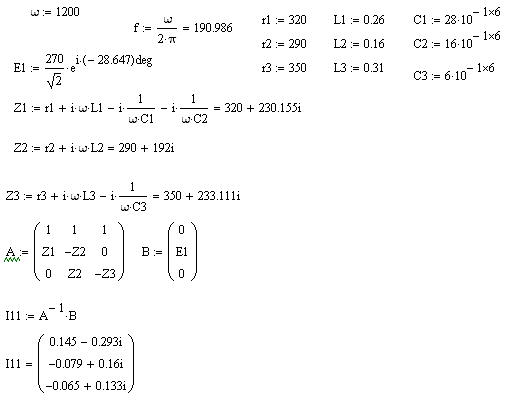
Рис. 4.3. Содержание программы расчета параметров электрической цепи в Mathcad.

Мощность источника переменного напряжения находится через умножение значения напряжения на сопряженное значение тока, проходящего через него

Мощность на потребителях в ветвях электрической цепи находится путем умножения их комплексного сопротивления на квадрат модуля тока проходящего через соответствующую ветвь.

Как мы видим: 51,112 + 35,82*j ≈ 51,072 + 35,796*j

Следовательно, уравнение баланса мощностей выполняется, а значит значения токов найдены правильно, ч.т.д.

4) После выполненного математического моделирования (см. рис. 4.1), были получены значения:

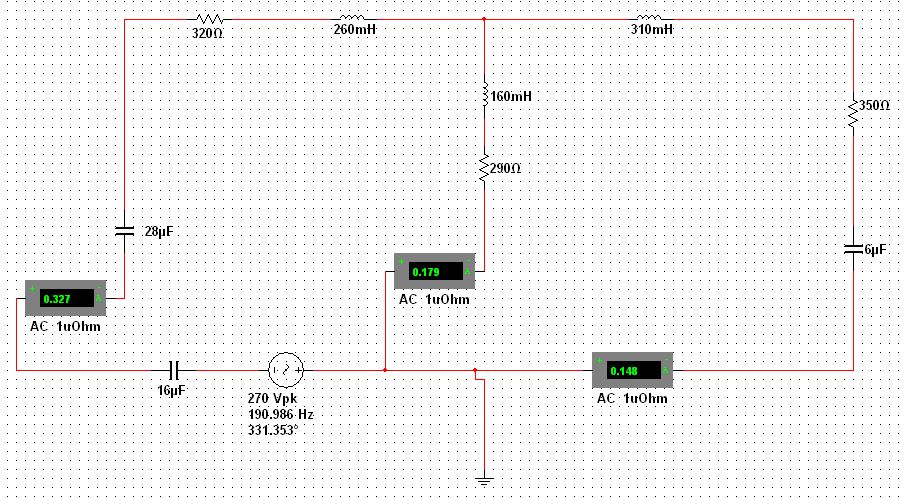
Рис. 4.3 – Данные полученные в результате математического моделирования.

Значения, полученные в результате расчетов, берем по модулю. Они равны:

I₁ = 0.237 А

I₂ = 0.178 А

I₃ = 0.148 А

Как мы видим, полученные результаты приблизительно совпали. Следовательно, расчеты были сделаны верно.

5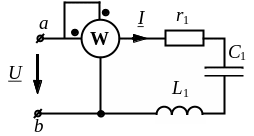 ) Для того что бы найти показание ваттметра, сначала мы найдем полное комплексное сопротивление данной цепи:

Z = r₁ + j*X_L1 - j*X_С1 = 320 + j*(312-29.7619) =

= 320 + j*282,2381

Найдем его модуль, и поделив на него напряжение мы сможем найти модуль тока.

Ом

I = U/Z = 0.632788 А

Как известно, ваттметр показывает лишь активную мощность, следовательно что бы найти показание прибора нужно активное сопротивление (резистор) умножить на квадрат тока, проходящего через потребитель.

P = I²*R =128,13474 Вт.

6) Измерить, с помощью виртуального ваттметра, в программе Multisim активную мощность в цепи (рис.2.2.). Полученное значение сравнить с пунктом 5. Сделать выводы.

Рис. 4.4 – Данные полученные в результате математического моделирования.

Полученное значение мощности приблизительно совпадает с расчетными данными. Значит, расчет был выполнен верно.

Заключение

В данной расчетно-графической работе мы исследовали электрические цепи постоянного и переменного тока.

Первая задача заключалась в изучении и нахождении параметров цепи постоянного тока. Согласно моему варианту, для данных схем были найдены искомые параметры. В первой схеме – найдено сопротивление цепи, и результат был проверен при математическом моделировании. Для второй схемы были найдены токи в ветвях. Правильность нахождения результата подтверждается уравнением баланса мощностей, и последующим математическим моделированием.

Вторая задача заключалась в исследовании электрических цепей переменного тока. В первой схеме необходимо было найти все сопротивления реактивных элементов. Далее с помощью данных, мы рассчитали комплексы сопротивлений, а затем и комплексы токов в каждой из ветвей. Для проверки было составлено уравнение баланса мощностей, которое было соблюдено, следовательно, расчеты были произведены правильно.

После этого мы провели компьютерное исследование в программе Multisim, используя данную нам цепь, используя данные по варианту. Значения токов при компьютерном исследовании цепи и полученные после расчетов данной по варианту различаются очень слабо, что подтверждает правильность расчетов.

В результате выполнения данной лабораторной работы весь теоретический материал был усвоен и использован в течении работы. Так же были приобретены навыки расчета цепей синусоидального тока, а так же закреплены навыки использования специального программного обеспечения, для расчетов электрических цепей - Multisim и Mathcad.

Список литературы

1. Теоретические основы электротехники: [в 3 т.]: учеб. для вузов: Т.1 / К.С. Демирчан [и др.]. – 4-е изд., доп. для самостоят. изучения курса; Гриф МО. – СПб.: Питер, 2006. - 462 с.

2. Алиев И. И. Электротехнический справочник / И. И. Алиев. - Изд. 4-е, испр. - М. : РадиоСофт, 2006. - 383 с. : ил. - Библиогр.: с. 377-379.

3. Матханов П.Н. Основы анализа электрических цепей: Линейные цепи: учеб. для вузов / П.Н. Матханов.-3-е изд., перераб. и доп. – М.: Высш. шк., 1990. – 400 с.

4. Прянишников В.А. Теоретические основы электротехники: курс лекций: учеб. пособие для вузов / В.А. Прянишников. -4-е изд. СПб.: КОРОНА принт, 2004. – 366 с.

5. Касаткин, А.С. Электротехника: учеб. для вузов / А.С. Касаткин, М.В. Немцов. – 9-е изд.– М.: Academia, 2005. – 639 с. (200 экз.)

6. Касаткин, А.С. Электротехника: учеб. для вузов / А.С. Касаткин, М.В. Немцов. – 8-е изд. испр. – М.: Академия, 2003. – 639 с. (7 экз.)

7. Касаткин, А.С. Электротехника: учеб. для вузов / А.С. Касаткин, М.В. Немцов. – 7-е изд. – М.: Высш. шк., 2003. – 542 с. (10 экз.)

8. Касаткин, А.С. Электротехника: учеб. для неэлектротехн. спец. вузов / А.С. Касаткин, М.В. Немцов. – 6-е перераб. изд. – М.: Высш. шк., 2000. – 542 с. (6 экз.)

9. Евдокимов, Ф.Е. Теоретические основы электротехники: учеб. для средн. проф. обр. / Ф.Е. Евдокимов – М.: Academia, 2004. – 560 c. (10 экз.)

10. Данилов, И.А. Общая электротехника с основами электроники / И.А. Данилов –М.: Высш .шк., 2000. – 752 с. (10 экз.)

11. Основы промышленной электроники: учеб. для вузов / В.Г. Герасимов, О.М. Князьков, А.Е. Краснопольский, В.В. Сухоруков. – М.: Высш. шк., 1986. – 336 с. (1 экз.)