4. Проверка гипотезы об адекватности модели

Гипотеза об адекватности модели проверяется с помощью критерия Фишера. Его расчетное значение определяется по формуле:

;

где

k – число коэффициентов регрессии.

Гипотезу об адекватности уравнения принимают в том случае, когда рассчитанное значение F- критерия не превышает табличного для выбранного уровня значимости, т.е когда

Если гипотеза об адекватности математической модели отвергнута, но максимальное относительное отклонение расчетного значения выходной характеристики от экспериментального не превышает 10-25% можно считать, что уравнение регрессии с достаточной точностью описывает изменение свойства объекта исследования и дает возможность использовать его для решения задач обеспечения надежности.

Максимальное относительное отклонение расчетного значения выходной характеристики от экспериментального вычисляется по формуле:

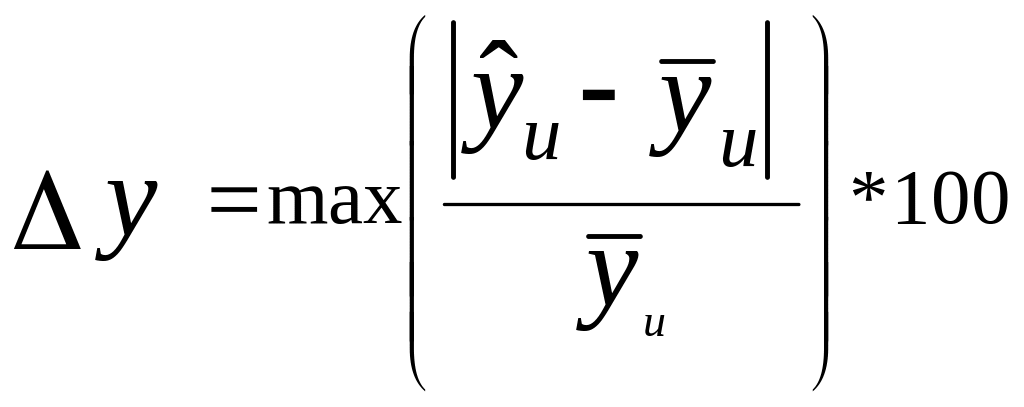Подставляя в найденную модель значения кодированных факторов в соответствии с матрицей плана(таблица 2), находим расчетные значения выходной характеристики , а также относительные ошибки. Результаты вычислений приведены в таблице 7.