
- •1.Потужність множини. Зчисленні множини та їх властивості. Зчисленність множини раціональних чисел.
- •Доведення Рефлексивність:
- •Транзетивність:
- •Доведення
- •Далі записуємо підряд всі числа, які є в таблиці
- •2.Незчисленні множини. Незчисленність множини дійсних чисел.
- •Доведення
- •3. Відображення множин (функції). Границя ф-ії та її неперервність. Різні означення та їх еквівалентність. Відображення множин (функції).
- •Границя ф-ії та її неперервність. Різні означення та їх еквівалентність.
- •Т.1 (перший критерій граничної точки).
- •Означення границі ф-ії по множині.
- •О.1’ .Означення границі ф-ії по Гейне (на мові послідовностей).
- •4. Класифікація функцій за їх властивостями.
- •Достатність.
- •Монотонні ф-ії
- •Парні та непарні ф-ії.
- •Періодичні ф-ії.
- •Теорема 4.(друга теорема Вейєрштрасса).
- •Т.5 (критерій неперервності монотонної ф-ії).
- •Т.6 (Кантора про рівномірну неперервність неперервної на сегменті ф-ії)
- •6. Поняття границі числової послідовності, її властивості.
- •7. Теорема Больцано-Вейєрштраса. Критерій Коші збіжної числової послідовності.
- •8. Означ. І вл. Рац степеня. Означення та степення з ірац показником. Степенева ф-я та її вл. Степенева ф-я в комплексній обл.
- •9. Показникова ф-я та її вл.. Розклад показн. Ф-ї в степен. Ряд. Показн. Ф-я компл. Обл.. Ф-ли. Ейлера.
- •10. Логарифмічна ф-я її властивості. Розклад логар. Ф-ї в степеневий ряд. Лог. Ф-я в компл. Обл. Інтегральне озн. Логарифма.
- •11. Тригонометричні ф-ї та їх властивості.
- •12. Похідна ф-ії однієї змінної, її геометричний і механічний зміст. Основні правила диференціювання.
- •1.Задача про миттєву швидкість матеріальної точки.
- •13. Диференційовані функції однієї змінної, критерій диференційовності. Диференціал в точці, його геометричний зміст, застосування до наближенихо бчислень. Диференціали вищих порядків.
- •15. Екстемуми ф-ії. Необхідні умови естемуму. Достатні умови екстремуму.
- •16. Опуклість, вгнутість та точки перегину графіка ф-ї.
- •17.Первісна ф-я та неознач. Інтеграл. Інтегрування підстановкою та частинами.
- •18.Означений інтеграл. Необхідна умова інтегрованості функцій. Критерій інтегровності. Інтегровн. Неперерв. Функції.
- •19. Означений інтеграл зі змінною верхнею межею, його властивості. Існування первісої для неперер ф-й. Ф-ла Ньютона-Лейбніца.
- •20. Поняття площі плоскої фігури. Квадрові фігури.Застосування означеного інтеграла
- •20. Поняття площі плоскої фігури. Квадрові фігури, застосування означеного інтеграла
- •21. Поняття кривої. Спрямлювані криві та їх довжини. Теорема Жордана. Обч. Довжини дуги при допомозі озн. Інтеграла.
- •22. Застос визн інтегр до обч тіл обертання та площ поверхонь обертання.
- •23. Додатні числові ряди, вл-ті збіжних рядів, критерій зб. Теореми про порівняння рядів. Ознака Даламбера та інтеграл. Ознака Коші.
- •24. Знакозмінні ряди. Ознака Лейбніца. Абсолютно та умовно збіжні ряди.
- •25. Функціональні послідовності і ряди. Збіжність, область збіжності. Рівномірна збіжність. Ознака Веєрштрса.
- •26. Степеневі ряди в комплексній обл. Круг збіжності.
- •28. Метричні простори. Відкриті та замкнені множини. Повні метричні простори.
- •29. Теорема Банаха про стиск відображення та її застосування.
- •30. Похідна функції комплексної змінної. Умови диферент.Поняття аналітичної функції.
7. Теорема Больцано-Вейєрштраса. Критерій Коші збіжної числової послідовності.
Т1.
(Больцано-Вейєрштраса)
Із будь-якої обмеженої послідовності
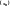 можна виділити збіжну підпослідовність.
Дов.
Нехай посл
можна виділити збіжну підпослідовність.
Дов.
Нехай посл
 обмеж, тобто існує відрізок
обмеж, тобто існує відрізок
 ,
що для всіх
,
що для всіх
 викон нерів
викон нерів
 .
Поділимо
.
Поділимо пополам. Тоді принаймні в одній половині
буде міст нескін м-на еле-ів посл
.
Позн цю половину
пополам. Тоді принаймні в одній половині
буде міст нескін м-на еле-ів посл
.
Позн цю половину
 .
Поділимо тепер відрізок
.
Поділимо тепер відрізок
![]() на два рівних відрізки і знову виберемо
той із них, у якому міститься нескін
множ елементів посл
на два рівних відрізки і знову виберемо
той із них, у якому міститься нескін
множ елементів посл .
Позначимо його
.
Позначимо його
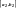 .
Продовжуючи цей процес, дістанемо
послідовність укладених відрізків
.
Продовжуючи цей процес, дістанемо
послідовність укладених відрізків ,
у яких довжина
,
у яких довжина
 -го
відрізка
-го
відрізка
 прямує до нуля при
прямує до нуля при
 .
Отже, за теоремою про вкладені відрізки
.
Отже, за теоремою про вкладені відрізки
 .
.
Побуд
підпосл посл
виконаємо так: у значенні
посл
виконаємо так: у значенні
 виберемо дов елемент із
,
який належ
,
у значенні
виберемо дов елемент із
,
який належ
,
у значенні

дов елемент із
дов елемент із
 ,
котрий належить відрізку
,
котрий належить відрізку
 і т. д. Оскільки для вибраних таким чином
елементів виконується нерівність
і т. д. Оскільки для вибраних таким чином
елементів виконується нерівність
 ,
то за теор. про границю проміжної
послідовності:
,
то за теор. про границю проміжної
послідовності:
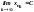 ,
отже
збіжна.
,
отже
збіжна.
Озн.
Послід.
наз. фундаментальною, якщо

Т2. (Кр.Коші). Для того, щоб послідовність була збіжною необхідно і досить, щоб вона була фундаментальною.
Дов.
Необхідність.
Нехай послідовність
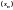 збіжна,
.
Тоді
збіжна,
.
Тоді .
Візьмемо
.
Візьмемо
 ,
,

 Тоді
Тоді

Достатність.
фундаментальна. Зафіксуємо деякий
номер
 ,
,
 ,
,
 Звідси випл що
обмеж посл. За попер теор з неї можна
вибрати збіжну підпосл. Нехай
Звідси випл що
обмеж посл. За попер теор з неї можна
вибрати збіжну підпосл. Нехай
 ,
це означає що
,
це означає що
 .
Доведемо, що
.
Доведемо, що
 .
Розглянемо:
.
Розглянемо:
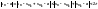 .
Якщо вибрати номер
.
Якщо вибрати номер
 ,
,
 ,
то
,
то
 .
Візьмемо довільне
.
Візьмемо довільне
 і поклад у попер міркув
і поклад у попер міркув
 ,
тоді
,
тоді
 .
.
Маємо,що .Це
означає, що
.Це
означає, що
8. Означ. І вл. Рац степеня. Означення та степення з ірац показником. Степенева ф-я та її вл. Степенева ф-я в комплексній обл.
Озн.
Нехай
 і
і
 ,
тоді розуміють
,
тоді розуміють

Озн.
Степенем числа
 з рац. показникам
з рац. показникам ,
де
,
де наз. число
наз. число .
Степінь числа 0 визначений тільки для
додатних показників.
.
Степінь числа 0 визначений тільки для
додатних показників.
 .
.
Зауваж.
Для - додатного і
- додатного і ,
число
,
число
 - додатне.
- додатне.
Зауваж.
Будь-яке рац. число можна записати по
різному у вигляді дробу, оце
 ,
для
,
для
 ,
значення а також не залежить від форми
запису рац. числа r.
,
значення а також не залежить від форми
запису рац. числа r.
Справді

Вл:
 -додатніх
-додатніх
1) Дов.
Дов.

2)
 ;
3)
;
3)
 ;
4)
;
4)
 ;
5)
;
5)
 ;
;
6)
Нехай
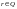 і
і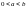 ,
тоді
,
тоді ,
якщо
,
якщо
 і
і ,
якщо
,
якщо .
.
7)
Для
 із неперервності
із неперервності
 ,
якщо
,
якщо
 і
і ,
якщо
,
якщо .
8)
.
8)
 .
.
Лема
1.
Для
 ,
при
,
при

Дов.
 (вл.8), тоді (за теор.)
(вл.8), тоді (за теор.)
 (озн. Гейне)
(озн. Гейне)

 -задов.
вибраній умові
-задов.
вибраній умові
 ,
,

 ;
;
 .
В силу обмеження
.
В силу обмеження

 -
сторонній корінь;
-
сторонній корінь;

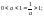

Лема2.
Якщо показникову ф-ю
розглядати як м-ну рац. чисел, то для
всякого іррац.


Озн.
Якщо
 -ірац.
число, то під степенем числа
-ірац.
число, то під степенем числа
 з показником
з показником
 розуміють число
розуміють число
 ,
,  ,
,
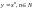 зростаюча і не перерв.
зростаюча і не перерв.
 тому для неї існує обернена яка є зрост.
і неперервною на
тому для неї існує обернена яка є зрост.
і неперервною на

 .
.
 -
обернена. Ф-я
-
обернена. Ф-я
 -
теж є визначеною і зрост. на
-
теж є визначеною і зрост. на
 ,
як композиція зрост. ф-й
,
як композиція зрост. ф-й
 .,
.,
 .
Крім того, ф-я
.
Крім того, ф-я
 є не перерв. на
то і
є не перерв. на
то і ,
як композиція неперервний ф-й є непер.
на
,
як композиція неперервний ф-й є непер.
на
 .
Все це справедливо і при
.
Все це справедливо і при
 ,
але при цьому треба розглядати м-ну
,
але при цьому треба розглядати м-ну
 .
.
Озн.
Ф-я
задана ф-єю
 ,
на степеневою з показником степеня
,
на степеневою з показником степеня
 .
.
Якщо
 ,
то степенева ф-я визначена і для
,
то степенева ф-я визначена і для
 бо
бо
 .
При цілих
.
При цілих
 степенева ф-я визначена і для
степенева ф-я визначена і для
 .
Для парних
,
ця ф-я парна, для непарних
-непарна.
Тому степеневу ф-ю достатньо
дослідити
на
.
Для парних
,
ця ф-я парна, для непарних
-непарна.
Тому степеневу ф-ю достатньо
дослідити
на
 .
.
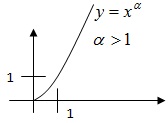
В
Л:

1) ,
2)
,
2) .
3)
.
3)

![]()
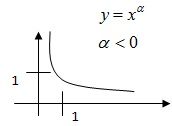
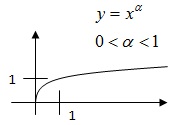
Теор.
Степенева
ф-я
 з
додатнім показником є зростаючою і
неперер. на
.
Якщо показник від’ємний то цей факт
справедливий на
з
додатнім показником є зростаючою і
неперер. на
.
Якщо показник від’ємний то цей факт
справедливий на
 і
ф-я спадатиме.
і
ф-я спадатиме.
В
комплексній обл.

1)
 -
однозначна
-
однозначна
2)
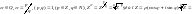
![]()

3)

 ,
де
,
де
 .
.
У цьому випадку ф-я є зліченою.
