28. Метричні простори. Відкриті та замкнені множини. Повні метричні простори.

Озн. Множина називається метричним простором, якщо за певним правилом у відповідності кожній впорядкованій парі ел-ів цієї множини поставлене дійсне число 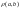, яке називається віддалю між елементами і і задовільняє умовам:

1) 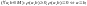2) 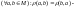симетр;

3) непер-сть.

Озн. Метричним простором називається сукупність , де - деяка множина, - метрика на цій множині.

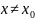Озн. Нехай U-деяка множина метричного простору M тоді називається граничною для множини U якщо в кожному околі точки принаймні 1-на точка , . Якщо точок 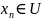яка збігається до .

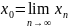
Озн. Нехай U множина точок метричного простору M. Тоді називається внутрішньою точкою множини якщо ця точка входить в множину з деяким своїм околом.Озн. Множина метричного простору називається замкненою, якщо вона містить в собі всі свої граничні точки.Озн. Множина G метричного простору називається відкритою якщо кожна точка цієї множини є її внутрішньою точкою.

Теор. Множина G метричного простору M є відкритою коли її доповнення множина замкнена.

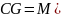
Теор. 1) Об’єднання скінченої сукупності замкнених множин є множиною замкненою.

2) Перетин довільної сукупності замкнених множин є множиною замкненою.

Д. 1) Дано: , - замкнена. Довести: - замкнена. - довільна гранична т. множини . Доведемо, що . Згідно означення:

. Всіх точок безліч, а множина скінчена к-сть, тому принаймні в одній з множині міститься нескінчена послід , . За властивістю: з того, що , то - гранична точка множини За умовою множини замкнені, то , а отже .

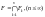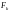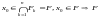2) Дано: , - замкнені. Довести: - замкнена. - гран т. множини . Покажемо, що - замкнені, то . - замкнена.

Теор. 1) Об’єднання довільної сукупності відкритих множин є множиною відкритою.

2) Перетин скінченої сукупності відкритих множин є множина відкрита.

Озн. Якщо в лінійно-нормованому просторі 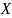кожна фундаментальна послідовність збіжна, то простір називають повним, або банановим.

Озн. Послідовність називається фундаментальною, або збіжною в собі якщо

Теор. В метр просторі збіжна послідовність є фундаментальною.

Озн. Послід 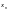точок метричного простору називається фундаментальною, якщо різниця 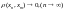, тобто .

Теор. В повному метричному просторі всяка послідовність вкладених одна в одну замкнених куль, радіуси яких і має єдину спільну точку.

Теор. Метричний простір є повним тоді і тільки тоді, коли стяжна система його замкнених куль має єдину спільну точку.

29. Теорема Банаха про стиск відображення та її застосування.

Розгл відобр дов метричного простору в себе. Їх наз операторами і позн . Пи розгл рівнянь є такі, які можна подати у вигляді (1), де - деяка точка з , -оператор з . Розв’язати (1) означає знайти ті точки , при яких (1) вірна. Їх наз розв’язками опер . Перед тим, як розв (1) треба дізнатись, чи має (1) розв’язок, скільки найпростіш це пит розв для операторів стиску.

О. Відобр метричного простору в себе наз оператором стиску, якщо

.

Кожне стиснуте відобр є неперерв відобр .

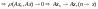Т. (Банаха) Всяке стискуюче відобр повного метр простору в себе має в просторі єдину нерухому точку.

Д. Проводиться методом послідовних наближень шуканої нерухомої точки, який полягає в тому, що будується послідовність, яка прямує до шуканої точки. Вона будується так:

Нех

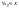
Покажемо, що ця послід фундамент в . Пок, що .

а)

б)

. Отже

(2); . Отже, ця послід фундамент. Оск простір повний, то посл є зб, тобто .

Т. є шуканою нерухомою точкою. Щоб в цьому переконатись, досить в посл перейти до границі. Але -неп оператор то при маємо:

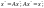
-нерухома точка відобр , і до того ж єдина. Якби поряд з нерухомою була б ще й т , то мали б: , .

Теор Банаха застосов при д-ні теореми про неявної ф-ї, при д-ні теор Пікара про розв’язку диф р-ня.