19. Означений інтеграл зі змінною верхнею межею, його властивості. Існування первісої для неперер ф-й. Ф-ла Ньютона-Лейбніца.

Озн. Нехай ф-я інтегровна на , тоді вона інтегровна і на і значить . Можна розглянути ф-ю - цю ф-ю наз. інтегралом із зміною верхнею межею.

Теор1.(основна теор інтегрального числення). Якщо ф-я інтегровна на , то ф-я неперервна на , якщо ж ф-я неперервна в т. і в деякому її околі, то ф-я диф. в т. і _{. .}

Дов. І. Треба показати, що вона неперервна в т. . А для цього треба показати, що її . Розглянемо . Оскільки інтегровна на , то вона обмежена цьому відрізку і значить . Тоді за теоремою за теор про проміжки значення - ф-я неперервна.

ІІ. Дано неперервна. Д-ти диференц. За теор. про середнє │ між та , що│ , тоді (2). Оскільк. Ф-я неперервна в т. , то при , т. (бо воно між ними), а ф-я неперер. то , отже в правій частині (2) . Тому і з ліва при і вона = . Таким чином, ф-я диференційовна і при чому . Т.д.

Наслідок.1. Якщо ф-я неперервна на , то вона має первісну на цьому відрізку і сукупність всіх неперервних задається ф-лою (3).

Дов. Справді із неперервності ф-ї на за теор.1 (ІІ частин.)ф-я є диференц. На , при чому . Це і означає, що ф-я є неперервною для . А тоді сукупність всіх неперервних задається формулою (3).

Наслідок.2.(ф-ла Н-Л) Якщо ф-я неперервна на , то де первісна ф-ї .

Справді, згідно Н.1. для ф-ї первісні на і множ. Всіх первісних зад формулою (3), підставимо в (3) , маємо: .

Тоді (3) запишемо так: .

20. Поняття площі плоскої фігури. Квадрові фігури.Застосування означеного інтеграла

Будемо вважати що кожен многокутник має площу. Фігура що має площу-квадровна. Розглянемо всі вписані іописані многокутники . Кожний многокутник має площу маємо . . Множина обмежена з верху площиною тому вона має . нижня площа ф-ри 0. Оскільки за озн. є найменша зверху межа мн. , а - довілна верхня межа, то множина обмежена знизу числом , тому множ. і цей є . У випадку коли фігура наз. квад подібною. А число S- називають її площею.

Теор. Плоска фігура є квадровною т. і т.т., коли послідовність многокутників і і таких

що і і вони рівні між собою. При цьому спільне значення цих = площі фігури .

Теор. Якщо ф-я невід’ємна і неперервна на , то криволінійна трапеція, яка обмежена з верху грофікрм цієї ф-ї є квадровною. І площа її обчислюється за ф-лою: .

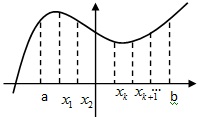Дов. Утвор дов. подін розглянемо суми Дарбу для цього поділу оскільки ф-я неперервна на , то вона но цьому відрізку також неперервна. І за критерієм інтегровності (1).

Геометрично являє собою площу деякої східчастої фігури, яка є многокутною вписаної в трапецію . Аналогічно площа східчастої фігури, тобто многокутника описаного навколо . Рівність (1) тоді буде означати, що площ східчастої фігури вписаних і описаних навколо , вони= інтегр. (1). Виберемо послідовний поділ , так що , тоді отримаємо послідовність многокутників вписаних і описаних навколо , які відповідають інтегральним сумам . Значить існує послідовність многокутників і і таких що на підставі рівності (1) при .. тоді за критерієм квадровності це і означає, що криволінійна трапеція квадровна і її площа= інтегралу (1). Т.д.(теор. довед.)