1. Потужність множини. Зчисленні множини та їх властивості. Зчисленність множини раціональних чисел.

2. Незчисленні множини. Незчисленність множини дійсних чисел. Множина потужності континууму.

3. Відображення множин (функції). Границя функції та її неперервність. Різні означення та їх еквівалентність.

4. Класифікація функцій за іх властивостями.

5. Основні властивості функції, неперервної на сегменті.

6. Поняття границі числової послідовності, її властивості. Поняття точної верхньої та точної нижньої граней числової множини. Існування точної верхньої грані числової множини, обмеженої зверху. Теорема про границю монотонної числової послідовності.

7. Теорема Больцано-Вейєрштрасса. Критерій Коші збіжної числової послідовності.

8. Означення і властивості раціонального степеня. Означення та існування степеня з ірраціональним показником. Степенева функція та її властивості. Степенева функція в комплексній області.

9. Показникова функція та її основні властивості. Розкладання показникової функції в степеневий ряд. Показникова функція в комплексній області. Формули Ейлера.

10. Логарифмічна функція та її властивості. Розкладання логарифмічної функції в степеневий ряд. Логарифмічна функція в комплексній області. Інтегральне означення логарифма.

11. Тригонометричні функції та їх властивості. Розкладання синуса та косинуса в степеневий ряд. Синус та косинус в комплексній області.

12. Похідна функції однієї змінної, її геометричний і механічний зміст. Основні правила диференціювання функцій. Похідні вищих порядків.

13. Диференційовні функції однієї змінної, критерій диференційовності. Диференціал в точці, його геометричний зміст, застосування до наближених обчислень. Диференціали вищих порядків.

14. Основні теореми диференціального числення. Теорема Лагранжа. Умови сталості та монотонності функції.

15. Екстремуми функції. Необхідні умови екстремуму. Достатні умови екстремуму.

16. Опуклість, вгнутість та точки перегину графіка функції.

17. Первісна функція та неозначений інтеграл. Основні методи інтегрування функцій.

18. Означений інтеграл. Необхідна умова інтегровності. Критерій інтегровності. Інтегровність неперервної функції.

19. Означений інтеграл із змінною верхньою межею, його властивості. Існування первісної для неперервної функції. Основна формула інтегрального числення (формула Ньютона-Лейбніца).

20. Поняття площі плоскої фігури. Квадровні фігури. Застосування означеного інтеграла до обчислення площ плоских фігур в декартових координатах.

21. Поняття кривої. Спрямлювані криві та їх довжини. Теорема Жордана. Обчислення довжини дуги при допомозі означеного інтеграла.

22. Застосування визначеного інтеграла до обчислення об’ємів тіл обертання та площ поверхонь обертання.

23. Додатні числові ряди, властивості збіжних рядів, критерій збіжності. Теореми про порівняння рядів. Ознака Даламбера та інтегральна ознака Коші.

24. Знакозмінні ряди. Ознака Лейбніца. Абсолютно і умовно збіжні ряди.

25. Функціональні послідовності і ряди. Збіжність, область збіжності. Рівномірна збіжність. Ознака Вейєрштрасса.

26. Степеневі ряди в комплексній області. Круг збіжності.

27. Формула і ряд Тейлора. Біноміальний ряд.

28. Метричні простори. Відкриті та замкнуті множини, їх властивості. Повні метричні простори.

29. Теорема Банаха про стискуючі відображення та її застосування.

30. Похідна функції комплексної змінної. Умови диференційовності. Поняття аналітичної функції.

1.Потужність множини. Зчисленні множини та їх властивості. Зчисленність множини раціональних чисел.

О.1 Кажуть, що між множинами встановлена взаємооднозначна вфдповідність, якщо задано взаємооднозначне (бієктивне) відображення мн. А на мн. В за певним правилом у відповіднсть кожному елементу 1-ої множини поставлено цілком певний ел. 2-ої мн. так, що:

1) по-перше, різним елемнтам відповідають різні елементи - ін’єктивність;

2) 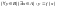- сюр’єктивність.

О.2 Якщо існує взаємооднозначне відображення мн. А на мн. Б, то кажуть, що мн. А і Б рівнопотужні (мають однакову потужність).

П-д. Множини з однаковою кількістю елементів завжди рівнопотужні.

Потужність скінченної мноижини – це кількість елементів множини.

Т.1 Поняття потужності множини в довільній сукупності множин задає відношення еквівалентності, тобто відношення множин є рефлесивним, симетричним та транзетивним.

Доведення Рефлексивність:

Бієктивне відображення мн. А на мн. А одержимо, якщо кожному елементу з мн поставимо той самий елемент .Симетричність:

Якщо , то існує бієктивне відображення мн. на і тоді , при чому бієктивно.

Транзетивність:

,

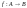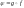Згідно з означенням існує , -бієктивне та бієктивне , оді відображення (композиція) відображає на .

Н.1 Поняття рівнопотужності множин дозволяє розбити довільну сукупність множин на класи еквівалентних між собою множин, які взаємно неперерізні і непорожні.

Кантор говорив, що потужність – це те спільне, що є в класі рівнопотужних між собою множин.

Якщо множини скінченні, то спільне є кількість елементів. Отже потужність нескінченних множин – це кількість елементів. Потужність скінченної множини – натуральні числа. Потужність нескінч. Мн. – кардиальні числа.

Т.2 Якщо дана сукупність взаємно неперерізних множин і сукупність взаємно неперізних мн. , і при , то .

О.3 Мн. назив. зліченню(зчисленною), якщо вона рівнопотужна множині натуральних чисел, тобто існує взаємооднозначне відображеня мн. на мн. натуральних чисел.

Очевидно, що мн. зліченна тоді і тільки тоді, коли її можна записати у вигляді послідовності 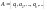. Спарвді, якщо мн. зліченна, то існує бієктивне відображення . При цьому відображ. деякий елем. . Навпаки .

Т.3 Із нескінченної мн. завжди можна виідлити скінченну підмн.

Доведення

Н.1 Кожна нескінченна підмножина зліченної множини є зліченою.

Н.2 Потужність (алеф нуль) зліченної множиниє найменшою із усіх потужностей зліченних множин є найменше кардинальн число з мн. потужностей.

П-ди:

1. Мн. чисел – зліченна.

2. Мн. чисел – зліченна.

3. Мн. чисел – зліченна.

– висота раціонального дробу (Кантор).

;

;

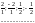
Далі записуємо підряд всі числа, які є в таблиці

Справді, яке б не було завжди знайдеться у виписаному стовбці висот. Кожній висоті відповідає скінченна кількість чисел і тоді стоїть в групі чисел, що має виоти, які відповідають скінченній групі чисел, значить є у цьому рядку і перед нею є скінченна кількість чисел.

Це означає, що має місце рівнвсть (1). .

Т.4 1. Об’єднання скінченної множини і здіченної множини є множиною зліченною.

2. Об’єднання зліченної сукупності скінченних множин є множиною зліченною або скінченною.

3. Об’єднання скінченної сукупності зліченних множин є множиною зліченною.

4. Об’єднання зліченної сукупності множин є множиною зліченною.

Т.5 Якщо мн. визначається скінченною кількістю індексів, що незалежно одна від одного пробігають зліченні множини, тобто якщо , то —зліченна.