Значение критерия Стьюдента -

Число степеней свободы	Уровень значимости (1-Р)
n–m – множественная корреляция n-1 – парная корреляция	0,05	0,02
1	12,706	31,821
2	4,303	6,965
3	3,182	4,541
4	2,776	3,747
5	2,571	3,365
6	2,447	3,143
7	2,365	2,998
8	2,306	2,896
9	2,265	2,821
10	2,228	2,764
11	2,201	2,718
12	2,179	2,681
13	2,160	2,650
14	2,145	2,624
15	2,131	2,602
16	2,120	2,583
17	2,110	2,567
18	2,101	2,552
19	2,093	2,539
20	2,086	2,528
Продолжение таблицы 5
21	2,080	2,518
22	2,074	2,508
23	2,069	2,500
24	2,064	2,492
25	2,060	2,485
26	2,056	2,479
27	2,052	2,473
28	2,048	2,467
29	2,045	2,462
30	2,042	2,457
	1,95996	2,32634

где 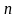- число наблюдений; 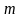- число параметров уравнения и - вероятность

8.7. Основные направления использования корреляционных моделей

В связи с тем, что сельскохозяйственное производство, особенно на современном этапе, представляет собой сложный материальный процесс, где формирование конечных показателей зависит от многих факторов, применение корреляционных моделей является здесь целесообразным и может принести существенную пользу.

Методологически определение и использование корреляционных моделей в основном осуществляется:

- для анализа хозяйственной деятельности сельскохозяйственных предприятий;

- для проведения плановых расчетов и получения нормативов;

- для прогнозирования социально-экономических явлений и процессов.

На всех этих направлениях наиболее часто используемыми являются факторные уравнения регрессии. В этом случае, исходная информационная база формируется на основе хозяйств района, зоны, края, республики. По исследуемой совокупности выявляется перечень основных факторов, определяющих урожайность сельскохозяйственных культур, продуктивность животных, производительность труда и других экономических характеристик. А на основе построенных моделей определяется эффективность факторов в различных районах, зонах.

Наряду с факторными уравнениями применимы динамические и автокорреляционные функции. Динамические функции выражают зависимость результативного признака 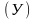от параметра времени с помощью различных уравнений трендов, и часто дают более высокие показатели тесноты связи, чем факторные. Еще более высокий индекс корреляции получают при использовании автокорреляционных моделей. В этом случае результативный признак рассматривается как функция от предыдущих по времени значений этой же переменной величины.

Есть исследования, рассматривающие все эти функции в совокупности, т.е. построение сложной экономической функции, имеющей элементы факторной, динамической и автокорреляционной моделей.

Важным аспектом является изучение корреляционных моделей в разрезе различных зон и регионов при одновременном исследовании их во времени. Это позволит выявить и обосновать перечень основных факторов формирования результативных экономических показателей (урожайности, продуктивности, себестоимости и др.), определить их эффективность в территориальном разрезе, изучить динамику их развития. Такие данные необходимы для анализа сложившихся экономических взаимосвязей, могут быть использованы для планирования, расчета нормативов (урожайности, продуктивности), прогнозирования социально-экономических явлений.

В связи с этим в ряде регионов страны созданы и создаются картотеки производственных сельскохозяйственных фикций, которые являются элементом создания автоматизированной системы управления народным хозяйством.

Сфера практического использования корреляционного моделирования очень обширна. Она в целом может быть разделена на 2 направления: первое - исследование макроэкономических процессов; второе - изучение микроэкономических явлений и процессов. В первом случае рассматриваются показатели народного хозяйства в целом или же в его основных отраслях. К таким процессам, по нашему мнению, можно отнести и комплексные исследования на уровне АПК края в целом, и вновь создаваемых производственных объединений "Изобильное", "Кировское", "Кубань" и т.д. Корреляционные модели здесь следует строить на основе укрупняющих факторов полученных путем предварительной статистической обработки (группировки, обработки динамических рядов, расчетов средних и т.п.) Типы проблем, а также конкретный набор зависимой и независимых переменных определяется исходя из целей исследования с учетом группировки факторов, приведенной в предыдущей таблице.

Большой интерес представляет здесь разработка таких моделей: "Валовая продукция, доход, прибыль - факторы интенсификации производства"; "Эффективность организации перерабатывающих предприятий и торговой деятельности"; "Зависимость цен от экономических условий"; "Зависимость изменений выпуска продукции от цен и других факторов"; "Зависимость взаимодействия спроса, предложения, цены и дохода"; "Формирование заготовительных квот"; "Определение нормативов коммунальных услуг, соцкультбыта и охраны окружающей среды".

Исследования микроэкономических явлений и процессов связаны с построением корреляционных моделей по отдельным предприятиям или даже подразделениям, большой интерес представляют также модели для отдельных технологических процессов и операций. Перечень проблем и набора переменных на этом уровне также чрезвычайно широк, но может быть во многом более детализированным с учетом рекомендаций, изложенных в разделе 8.1.

Особо следует отметить проблему, актуальность которой выдвинулась на первый план - нормативное планирование. Достаточная обоснованность нормативов, являющаяся главным условием их успешного применения, объективно может быть достигнута лишь на основе тщательного качественного и количественного анализа многих факторов, что предопределяет необходимость корреляционного моделирования на базе современной электронно-вычислительной техники.

Разумеется самое широкое применение корреляционное моделирование может найти и во многих других сферах научной, технической и практической деятельности людей.