Корреляционно-регрессионный анализ

Матрица корреляции
Строка	1	1,000	0,724	0,801
Строка	2	0,724	1,000	0,746
Строка	3	0,801	0,746	1,000

Таблица 18

Статистические характеристики

Номер перемен.	Среднее значение		Ср. кв. отклонение	Пар. Кор Х У		Коэффиц. регрессии	Значение кр.Стьюдента
2	65,60000		10,93357	0,72417		0,11284	1,16356
3	1,45400		0,47785	0,80051		5,28888	2,38350
Зависимая переменная
1	31,41334		4,30662
Своб. член =16,32095		Множ. корр.=0,82294			Детерминация=0,677225

Таблица 19

Анализ взаимосвязей

Номер перемен.	Эластичность	Номер. коэф. линии регрес.	Порцион. коэф. детерминации
2	0,23564	0,28648	0,20746
3	0,24480	0,58684	0,46977

Если - колеблемость небольшая; 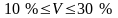- колеблемость средняя; - колеблемость большая.

Для данного случая имеем

,

,

,

т.е. в исследуемой совокупности колеблемость урожайности и балльной оценки пашни является средней, а колеблемость доз внесения минеральных удобрений - большой. Далее приводятся значения парных коэффициентов корреляции для соответствующих переменных (“ ”), характеризующие тесноту связи между У и соответствующим значением X . В результате получим

; .

Здесь же печатаются вычисленные значения параметров (“коэффициентов регрессии”) , а также значение параметра (“свободный член”) (в нашем примере ; ; ).

Используя вычисленные значения этих коэффициентов строят корреляционную модель (уравнение).

Для данного случая имеем

.

В этом же разделе даются значения коэффициентов множественной корреляции (“множ. корр.”) и коэффициента детерминации (“детерминация”) по которым оценивается теснота связи и доля влияния на общую вариацию факторов включенных в модель. для рассматриваемого случая

; ,

т.е. связь тесная, а факторы, включенные в модель, примерно на 68 % определяют изменение урожайности. (При связь между факторами оценивается как слабая, при - как заметная, - существенная, - тесная, - очень тесная).

Приводимые в этом разделе значения критерия Стьюдента можно также использовать для оценки существенности влияния факторов включенных в модель. При делается заключение о существенности фактора. Для данного примера при уровне значимости 0,05 (95 % вероятность), 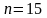, имеем:

;

,

Раздел "Анализ взаимосвязей" включает в себя значения коэффициентов эластичности для соответствующих значений переменных, - коэффициенты (нормир. коэф. линии регресс.) и коэффициенты частной детерминации (порцион. коэф. детерминации). Их сущность и экономический смысл излечены в разделе 8.3. В рассматриваемом примере ; ; ; , т.е. влияние второго фактора (доз внесения удобрений) более существенно, поскольку и .

Таблица 20