
- •8. Способы изучения стохастических связей в анализе хозяйственной деятельности
- •8.1. Сфера и цели применения стохастического анализа
- •8.2. Проблемы отбора совокупности обследования
- •8.3. Этапы корреляционного моделирования
- •1. Формирование статистической совокупности для исследований.
- •2. Установление математической формы связи между изучаемыми признаками.
- •8.4. Формирование статистической совокупности для исследований
- •Матрица исходных данных
- •Рекомендуемые наборы переменных для корреляционного анализа
- •8.5. Установление математической формы связи между изучаемыми признаками
- •8.6. Анализ характеристик корреляционной модели
- •Матрица парных коэффициентов корреляции
- •Матрица исходных данных
- •Исходные данные для регрессионного анализа
- •Корреляционно-регрессионный анализ
- •Статистические характеристики
- •Анализ взаимосвязей
- •Значение критерия Стьюдента -
- •8.7. Основные направления использования корреляционных моделей
8.5. Установление математической формы связи между изучаемыми признаками
Целью данного этапа является нахождение конкретного математического выражения функции:
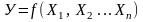 .
.
В данном случае наиболее сложной проблемой является выбор формы связи (типа аналитического уравнения – прямолинейная зависимость, криволинейная зависимость и т.д.) выбор типа функции должен опираться на теоретические исследования или же находиться путем последовательного подбора различных типов уравнений.
При выборе уравнений можно использовать некоторые общие приемы: графический анализ, с целью выявления характера зависимости между зависимыми парами переменных; выбор простейших видов функций, а при выявлении их непригодности переход к более сложным уравнениям; выявление наиболее пригодного типа функции путем сравнения оценок тесноты связи и статистической надежности как уравнения в целом так и его отдельных параметров (коэффициентов регрессии).
При парных корреляционных связях наиболее часто используют следующие типы функций:
 -
уравнение прямой,
-
уравнение прямой,
 -
уравнение параболы второго порядка,
-
уравнение параболы второго порядка,
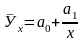 -
уравнение гиперболы,
-
уравнение гиперболы,
 -
уравнение показателей кривой –
экспоненты.
-
уравнение показателей кривой –
экспоненты.
Для
аппроксимации фактических данных
используют полиномы П.Л. Чебышева:
 .
.
Повышение порядка полинома производят до тех пор, пока остаточная дисперсия продолжает уменьшаться. Если при переходе к уравнению регрессии более высокого порядка остаточная дисперсия уменьшается незначительно, то аппроксимацию считают достаточной.
Учитывая, что на практике путем математических преобразований многие функции можно привести к линейному виду, рекомендуется построение уравнений множественной регрессии в линейной форме
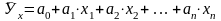 .
.
Сформированная статистическая совокупность и подобранная форма уравнения позволяют перейти к расчету параметров модели. Для расчетов параметров разработаны различные методы, однако практически чаще всего используют метод наименьших квадратов. Суть его в том, чтобы сумма квадратов отклонений фактических данных от исчисленных по выбранному уравнению была наименьшей.
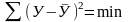 .
.
При использовании метода наименьших квадратов получают системы «нормальных» уравнений. Например, при использовании в качестве формы связи уравнения прямой после необходимых преобразований получают следующую систему «нормальных» уравнений
 .
.
Для
множественной корреляционной зависимости
при n-ом
количестве факторов (
)
для определения параметров уравнения
регрессии также необходимо составить
систему «нормальных» уравнений, которая
содержит (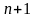 )
линейное уравнение с (
)
неизвестными параметрами
)
линейное уравнение с (
)
неизвестными параметрами

Решение системы «нормальных» уравнений при значительном количестве параметров функции представляет некоторые трудности в вычислении. Поэтому, расчеты параметров уравнений модели корреляционной зависимости и других характеристик модели целесообразно производить с использованием ЭВМ.
8.6. Анализ характеристик корреляционной модели
Основными показателями, получаемыми в результате корреляционно-регрессионного анализа, являются коэффициенты регрессии и коэффициенты корреляции.
Анализ
экономической интерпретации коэффициентов
регрессии (параметров уравнения
 )
дает основание сформулировать общее
определение его смысла. Коэффициент
регрессии показывает, к какому изменению
средней величины результативного
признака приводит изменение факторного
признака на одну единицу. Так, если при
изучении корреляционной связи между
урожайностью (У,
ц/га) и дозами вносимых удобрений (Х,
ц д.в. на 1 га) получено следующее уравнение
регрессии:
)
дает основание сформулировать общее
определение его смысла. Коэффициент
регрессии показывает, к какому изменению
средней величины результативного
признака приводит изменение факторного
признака на одну единицу. Так, если при
изучении корреляционной связи между
урожайностью (У,
ц/га) и дозами вносимых удобрений (Х,
ц д.в. на 1 га) получено следующее уравнение
регрессии:
 ,
,
Судя
по уравнению, можно сказать следующее:
увеличение внесения удобрений на одну
единицу размерности (на 1 центнер)
повлечет за собой изменение (в данном
случае рост) урожайности на 1,02 ц/га, т.е.
на величину коэффициента регрессии
 .
.
Таким образом, коэффициенты регрессии выступают в качестве показателей влияния или эффективности факторов.
Насколько правдоподобно коэффициенты регрессии отражают эффективность, отзывчивость факторов, зависит, правильно ли подобрана форма связи и какие факторы включены в модель.
Условный эффект фактора отражает коэффициент парной регрессии, т.е. в нашем примере коэффициент регрессии 1,02 характеризует влияние доз удобрений (чистое влияние) на урожайность и одновременно влияние других факторов, корреляционно связанных с дозами удобрений, и через этот фактор также влияющих на урожайность. Поэтому и считают, что коэффициент парной регрессии отражает условную эффективность фактора.
Чистую эффективность фактора может выражать коэффициент множественной регрессии при условии, что в подобранную модель включены все факторы, влияющие на анализируемый результативный признак. В этом случае влияние всех факторов выявляется в чистом виде, т.к. эффект каждого фактора «очищен» от влияния других, имеющих с ними корреляционную связь, ибо в уравнение включены все факторы.
Однако особенностью агроэкономических явлений является то, что в их формировании принимает участие чрезвычайно много факторов. Включить их все в одну модель практически невозможно. Поэтому различают относительно чистую эффективность коэффициентов множественной регрессии, которые получают в случае, когда в уравнение включены основные факторы, влияющие на результативный признак, и форма связи подобрана правильно. Каждый из коэффициентов такой модели характеризует не только «чистый» эффект фактора, но также и влияние корреляционно связанных с ним факторов, но не вошедших в данное уравнение регрессии. При этом каждый коэффициент регрессии «очищен» от влияния других факторов, входящих в уравнение регрессии. И чем правильнее и полнее выбраны и учтены основные наиболее существенные факторы, тем реальнее коэффициенты регрессии отражают чистую эффективность.
Для измерения тесноты связи между У и факторами, вошедшими в модель используют парные, частные и множественные коэффициенты корреляции. При линейной форме зависимости, показатели тесноты связи называют коэффициентами, при криволинейной – индексами. Линейные коэффициенты корреляции являются частным случаем индекса корреляции. Значение показателей тесноты связи в том, чтобы отразить, какую часть общей вариации результативного признака У можно объяснить независимым признаком Х, входящим в соответствующее уравнение регрессии. Измерение тесноты связи основано на сопоставлении показателей вариации результативного признака (У). Для этих целей исчисляют общую дисперсию
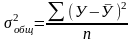 ,
,
характеризующую общую вариацию результативного признака (У), объясняемую влиянием всех факторов, от которых он зависит.
Факторную дисперсию исчисляют по формуле:
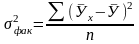 ,
,
которая характеризует вариацию (У), объясняемую только фактором (Х) или факторами ( ), соответственно для парной и множественной корреляции.
В связи с этим для измерения тесноты связи используют отношение факторной дисперсии к общей дисперсии результативного признака. Это отношение называют индексом детерминации
 .
.
Корень квадратный из данного выражения называют индексом корреляции.
 .
.
Подобно тому, как коэффициенты парной и множественной регрессии отражают условную и условно-чистую эффективность факторов, так парные и частные коэффициенты корреляции и детерминации характеризуют тесноту связи между (У) и факторами-аргументами ( ), вошедшими в модель.
Особо
важное значение, имеет определение
парных коэффициентов корреляции при
отборе факторов. Для этого строится
матрица парных коэффициентов корреляции,
измеряющих тесноту линейной связи между
результативным признаком (У)
и каждым фактором-аргументом (Х),
а также между факторами аргументами,
т.е. между показателями
 ,
,
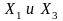 ,
,
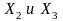 и т.д.
и т.д.
Таблица 15
