Тырсин А.Н. Учебное пособие по дискретной математике

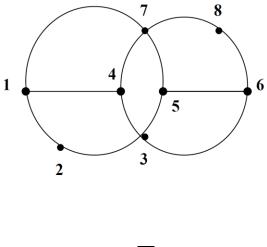
Пример 10.2. Найти диаметр, центры, диаметральные и радиальные цепи графа, изображенного на рис. 10.4.

Рис. 10.4. Неориентированный граф

Решение. Перенумеруем вершины графа. Найдем расстояния между всеми вершинами графа: d (i, j) , i, j 1,8. Образуем из полученных вершин

матрицу расстояний {d(i, j)}. Матрицу расстояний удобно использовать для определения диаметра, радиуса и других величин. Она будет иметь следующий вид:

Найдем максимальный по величине элемент матрицы расстояний:

max d (i, j) 3.

i, j 1, ,8

В соответствии с данным выше определением диаметр графа равен 3. Диаметральные цепи имеют длину равную 3 и соединяют вершины 1 и 6, а также 2 и 8 (эти вершины находим с помощью матрицы расстояний: определяем строки и столбцы, соответствующие расстоянию, равному диаметру). Соответствующие диаметральные цепи графа, выраженные через вершины, имеют вид: (1, 7, 5, 6), (1, 4, 3, 6), (1, 7, 8, 6), (1, 2, 3, 6), (2, 1, 7, 8), (2, 3, 6, 8).

Определим для каждой вершины графа максимальное удаление. Для этого достаточно найти максимальную величину в каждой из строк матрицы расстояний: r(1) = 3, r(2) = 3, r(3) = 2, r(4) = 2, r(5) = 2, r(6) = 3, r(7) = 2, r(8) = 3. Из полученных величин выберем минимальное значение

71

min r(i) 2 .

i 1, ,8

Таким образом, радиус графа равен 2. Максимальное удаление, равное радиусу графа, имеют вершины 3, 4, 5, 7. Они будут центрами графа. Укажем радиальные цепи для вершины 3: (3, 2, 1), (3, 4, 1), (3, 4, 7), (3, 5, 7), (3, 6, 8). Как и диаметральные цепи, они записаны с помощью номеров вершин.

10.4. Эйлеровы циклы

Цикл, содержащий все ребра графа, называется эйлеровым циклом. Граф, имеющий эйлеровые циклы, называется эйлеровым графом.

Теорема 10.1. (Теорема Эйлера). Конечный неориентированный граф является эйлеровым тогда и только тогда, когда он связан, и степени всех его вершин четны.

Примем без доказательства.

Пример 10.3. Возвращаясь к графу задачи о кенигсбергских мостах (рис. 9.5), заметим, что во-первых, данный граф связный, а, во-вторых, степени всех его вершин нечетны. Из теоремы Эйлера следует, что осуществить задуманный обход мостов невозможно.

Известен следующий нерекурсивный алгоритм Флери построения эйлерова цикла:

1.Начать цикл с произвольной вершины u. Присвоить произвольному ребру uv, инцидентному u, номер 1. Удалить из графа ребро uv, перейти в вершину v.

2.Пусть после k шагов мы находимся в вершине w. Выбрать произвольное ребро wt, причем мост выбирается только в том случае, если нет другой возможности. Ребру wt присвоить номер k + 1. Удалить из графа ребро wt, перейти в вершину t.

Число шагов в описанном алгоритме совпадает с числом ребер в графе. По окончании работы алгоритма ребра исходного графа будут пронумерованы в порядке их следования в эйлеровом цикле.

Определение 10.4. Гамильтонов цикл – простой цикл, проходящий через все вершины графа. Гамильтонова цепь – простая цепь, проходящая через все вершины графа, с началом и концом в разных вершинах.

Пример 10.4. Применим понятие эйлерова цикла к решению задачи о планировании маршрута подметальной машины в небольшом городке. Схема улиц этого городка в виде графа представлена на рис. 10.5. Улицам

72

соответствуют ребра, перекресткам – вершины графа. Слева и снизу от изображения графа в масштабе указаны расстояния между перекрестками. Движение подметальной машины начинается и заканчивается в вершине 1 (гараж). Необходимо спланировать маршрут подметальной машины таким образом, чтобы все улицы городка были подметены при минимальном холостом пробеге машины.

Рис. 10.5. Схема улиц в виде графа

Решение. В графе четыре вершины нечетной степени: 9, 6, 2, 3. Граф не является эйлеровым, поэтому в нем нет маршрута, начинающегося и заканчивающегося в вершине 1 типа эйлерова цикла. Если соединить вершины нечетной степени попарно дополнительными ребрами, проходящими по улицам, то получим эйлеров граф, в котором существует маршрут, проходящий по каждому ребру (основному и дополнительному) только один раз. Поскольку подметальная машина должна по условию задачи вернуться в гараж, то по некоторым улицам ей придется проехать, по крайней мере, два раза. Очевидно, что маршруты по дополнительным ребрам должны обладать минимальными длинами.

Рассмотрим возможные случаи попарных соединений вершин с нечетными степенями дополнительными ребрами. Таких случаев три.

1. Дополнительные ребра, соединяющие вершины 9 и 2 и вершины 6 и 3, можно представить кратчайшими маршрутами из основных ребер графа:

2.Дополнительные ребра, соединяющие вершины 9 и 6 и вершины 2 и 3, можно представить кратчайшими маршрутами из основных ребер графа: (10, 11) и (2). Это приведет к холостому пробегу в 1 + 2 + 3 километров.

3.Дополнительные ребра, соединяющие вершины 9 и 3 и вершины 6 и 2, можно представить кратчайшими маршрутами из основных ребер графа:

73

(12, 7, 5) и (8, 9). Это приведет к холостому пробегу 1 1 8 2 2 километров.

Сравним длины холостых пробегов для перечисленных случаев. Самый короткий холостой пробег получится во втором случае – 6 километров. Оптимальный маршрут подметальной машины изображен на рис. 10.6.

Рис. 10.6. Оптимальный маршрут подметальной машины

Он представляет собой последовательность ребер (1, 2, 3, 4, 5, 2, 9, 7,

6, 10, 11, 12, 8, 10, 11, 13).

74

Индивидуальное задание

Раздел I. Введение в теорию множеств

1. Задачи № 1-20

Осуществить операции над множествами A, B, если

U = {1,2,3,4,5,6,7,8,9}:

2. Задачи № 21-40

Используя диаграммы Венна, решить задачи:

21.Каждый из 500 студентов обязан посещать хотя бы один из трех спецкурсов: по математике, физике, астрономии. Три спецкурса посещают 10 студентов, по математике и физике – 30, по математике и астрономии – 25; только спецкурс по физике – 80 студентов. Известно также, что спецкурс по математике посещают 345 студентов, по физике – 145, по астрономии – 100 студентов. Сколько студентов посещают только спецкурс по астрономии? Сколько студентов посещают два спецкурса?

22.500 студентов посещают три спецкурса. Спецкурс только по математике, только по математике и физике и только по физике и астрономии посещают одинаковое число студентов; три спецкурса посещают 20 студентов. Спецкурс по математике посещают столько же студентов, сколько спецкурс по физике. Один спецкурс по физике посещают 50 студентов, а спецкурс по астрономии – 250 студентов. Сколько студентов посещают только один спецкурс?

23.Экзамен по математике содержал три задачи: по алгебре, по геометрии и по тригонометрии. Из 750 абитуриентов задачу по алгебре решили 400 абитуриентов, по геометрии – 480, по тригонометрии – 420; задачи по алгебре или геометрии решили 630 абитуриентов; по геометрии или тригонометрии – 600 абитуриентов; по алгебре или тригонометрии –

75

620 абитуриентов; 100 абитуриентов не решили ни одной задачи. Сколько абитуриентов решили все задачи? Сколько решили только одну задачу?

24.Экзамен по математике содержал три задачи: по алгебре, по геометрии и по тригонометрии. Из 800 абитуриентов задачу по алгебре решили 250 абитуриентов, по алгебре или геометрии – 660; по две задачи решили 400 человек, из них задачи по алгебре и геометрии решили 150 человек, по алгебре и тригонометрии – 50 человек; ни один абитуриент не решил все задачи; 20 абитуриентов не решили ни одной задачи; только задачу по тригонометрии решили 120 человек. Сколько абитуриентов решили только одну задачу? Сколько абитуриентов решили задачу по геометрии?

25.На кафедре иностранных языков работают 18 преподавателей, из них 12 преподают английский язык, 11 – немецкий, 9 – французский; 5 преподавателей преподают английский и немецкий языки, 4 – английский

ифранцузский, 3 – немецкий и французский. Сколько преподавателей преподают все три языка? Только два языка?

26.На кафедре иностранных языков работают 37 преподавателей, из них французский язык преподают 23 преподавателя, английский язык – 16 преподавателей, все три языка – три преподавателя. Число преподавателей, ведущих занятия только по английскому языку, равно числу преподавателей, ведущих занятия только по немецкому языку. Число преподавателей, ведущих занятия только по английскому и немецкому языкам, равно числу преподавателей, ведущих занятия только по немецкому и французскому языкам. Сколько преподавателей преподают один иностранный язык? Сколько преподавателей преподают один английский язык?

27.На курсах иностранных языков учится 600 человек, из них французский язык изучают 220 человек, английский – 270 человек, слушатели, изучающие английский язык, не изучают немецкий язык; один французский язык изучают 100 человек, один немецкий – 180 человек. Сколько человек изучает по два иностранных языка? Сколько человек изучает один иностранный язык?

28.Группа студентов из 25 человек сдала экзаменационную сессию со следующими результатами: 2 человека получили только «отлично», 3 человека получили отличные, хорошие и удовлетворительные оценки; 4 человека – только «хорошо»; 3 человека – только хорошие и удовлетворительные оценки; число студентов, сдавших сессию только на «отлично» и «хорошо», равно числу студентов, сдавших сессию только на «удовлетворительно». Студентов, получивших только отличные и удовлетворительные оценки – нет. Удовлетворительные или хорошие оценки получили 22 студента. Сколько студентов не явилось на экзамены? Сколько студентов сдали сессию только на удовлетворительно?

76

29.На курсы иностранных языков зачислено 300 слушателей. Из них французский или английский изучают 250 человек, английский и немецкий

–60 человек, английский и французский – 80 человек; число слушателей, изучающих только французский язык, равно числу слушателей, изучающих только немецкий язык; 70 человек изучает только английский язык. Занятия по французскому и немецкому языкам проводятся единовременно. Сколько слушателей изучает немецкий язык или французский? Сколько слушателей не посещает занятия?

30.Преподаватели кафедры прикладной математики преподают на трех факультетах: механическом, технологическом, экономическом. На технологическом факультете работает 22 преподавателя, на механическом

–23 преподавателя, на механическом и экономическом – 36 преподавателей; только на технологическом факультете – 10 преподавателей; 2 – на трех факультетах; 5 преподавателей работают только на механическом и экономическом факультетах. Число преподавателей, работающих только на механическом и технологическом факультетах, равно числу преподавателей, работающих на экономическом и технологическом факультетах. Сколько преподавателей работает на кафедре? Сколько преподавателей работает только на одном факультете?

Упростить выражение:

31.( A \ B \ B C) \ C D .

32.(A A B A C) A B \ C .

33.A \ B C \ A B C A B C .

34.A A B B C \ A .

35.A ( A \ B) ( A \ B) .

36.A \ B C \ A B C A B C .

37.A B B C \ B .

38.(A A B A C) A B C .

39.(A B C) \ (B C A B C) (A B C).

40.(A (B \ A) A C) A C \ C .

3.Задачи № 41-60

41.Назвать отношения R , R–1, R(2), Ro, R , если отношение R означает: а) «быть братом», б) «быть сыном». Каковы свойства этих отношений?

42.Назвать отношения R , R–1, R(2), Ro, R , если отношение R означает: а) «жить в одном городе», б) «быть частью целого». Каковы свойства этих отношений?

43.Пусть (M) – множество всех подмножеств, составленных из

элементов множества M = {a, b, c}. Задать списком отношение R,

77

47.Пусть M = {1, 3, 5, 7} и отношение R M M. Задать списком отношения R, R–1, R , транзитивное Ro и рефлексивное R замыкания, если:

а) R = {(a, b): a b}; б) R = {(a, b): (a + b) /2 M}; в) R = {(a, b): a – 1 = b}.

48.Пусть M = {1, 3, 5, 7} и отношение R M M. Задать списком отношения R, R–1, дополнение R , транзитивное Ro и рефлексивное R

б) R = {(A, B): A B }; в) R = {(A, B): A B = и A B = U}.

51. Чему равна композиция функций f(x) и g(x), если: а) f(x) = 2x, g(x) = lgx; б) f(x) = x3, g(x) = x ; в) f(x) =3x, g(x) = x + 1.

Каковы области определения функций и их композиций?

52. Чему равна композиция функций f(x) и g(x), если: а) f(x) = 3x + 1, g(x) = sinx; б) f(x) = 2x, g(x) = x ; в) f(x) = x2, g(x) = x + 1.

Каковы области определения функций и их композиций?

53.Являются ли коммутативными бинарные арифметические операции на множестве натуральных чисел N? Ответ проиллюстрировать на примерах.

54.Являются ли коммутативными бинарные операции над множествами? Ответ проиллюстрировать на примерах.

55.Показать дистрибутивность справа и слева операции умножения относительно сложения на множестве N. Является ли дистрибутивной справа (слева) операция возведения в степень относительно умножения, операция сложения относительно умножения?

78

56.На множестве целых чисел определено отношение «сравнимости по модулю натурального числа n»: x y(mod n) тогда и только тогда, когда (x – y) делится на n. Определить свойства отношения (рефлексивность, симметричность и др.).

57.На множестве M = {1, 2, 3, 4, 5, 6} построить матрицу бинарного

отношения R = {(a, b): a + b 5, a, b M}.

58.На множестве M = {1, 2, 3, 4, 5, 6} построить матрицу бинарного отношения R = {(a, b): 1 a – b 5, a, b M}.

59.Пусть R1, R2 – бинарные отношения, определенные на множестве

(составного отношения), т.е. R1 R2 R2 R1, если: R1 – «быть больше», R2 – «иметь общий делитель, отличный от 1».

Раздел II. Математическая логика

4. Задачи № 61-80

Построить таблицу истинности для формул:

61.(((C B) B) (A B)) C .

62.((C B) A) (A B C) .

63.((A B) C) B (A C) .

64.(B C) (C A) (A B).

65.(A B C) (A C B) .

66.(A C) (B C A) B .

67.(C A B) (B C A) .

68.(A B C) (B C) A .

69.((C A B) A) (A B) .

70.((Α Χ Β) Χ ) (Β Α) .

71.((C (B A)) (A C)) B .

72.(A C) (B A) (B C) .

73.(A B C) (B C A) .

74.(A C B) ((B A) C) .

79

75.(B A C) (C B A) .

76.(C B A) (C B) A.

77.(C (B A)) A B C .

78.(A C) (B A) (C A) .

79.(B A C) ((A C) B) .

80.A ( A B C) (B C) .

5. Задачи № 81-100

Записать логическую функцию F трех переменных, заданную таблично, в виде СДНФ.

6. Задачи № 101-120

Преобразовать к ДНФ, СДНФ, КНФ, СКНФ формулы:

101.( A B B C C A) ( A B C) .

102.( A B C B) ( A B B C) .

103.(B A A C) (C B A) .

104.(A B C) (A B C) .

105.( A B) ( A C) ( A C) B .

106.(C A B) ( A C) (B C) .

80