Тырсин А.Н. Учебное пособие по дискретной математике

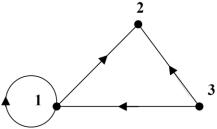
Пример 9.7. Выпишем матрицы смежности для графов, изображенных на рис. 9.6, 9.7 соответственно:

Матрица смежности так же, как и матрица инцидентности, определяет соответствующий неориентированный или ориентированный граф. Число его вершин равно размерности матрицы n, i-й и j-й вершинам инцидентныij ребер. Для неориентированного графа ij = ji,

В случае представления графа списком ребер отношение инцидентности задается списком ребер графа. Список ребер графа представляется двумя столбцами:

-в левом перечисляются все ребра ei E;

-в правом – инцидентные соответствующему ребру вершины v j , v j .

Для неориентированного графа порядок вершин в строке произволен. Для ор-графа вначале должен стоять номер начала ребра.

9.3. Достижимость

Представим граф G = V, E в другой форме:

G = G(V, Г(V)),

где V – множество вершин v1, , vn графа G, Г(V) – отображение множества V на себя.

Пример 9.8. Построить ор-граф G, заданный множеством вершин

V = {v1, v2, v3} и отображениями Г(v1) = {v1, v2}, Г(v2) = , Г(v3) = {v1, v2}.

Данный граф представлен на рис. 9.8.

Рис. 9.8. Ор-граф

61

Вершина графа vj называется достижимой из вершины vi того же графа, если существует по крайней мере один путь из vi в vj.

Множество вершин R(vi), достижимых из некоторой вершины vi V, определяется следующим выражением

Действительно, первым элементом множества R(vi) является вершина vi, которая достижима из себя самой с помощью пути длины нуль; Г(vi) – множество вершин vj, достижимых из vi с использованием путей длины единица; Г2(vi) – множество вершин vj, достижимых из vi с использованием путей длины два; ; Гp(vi) – множество вершин vj, достижимых из vi с использованием путей длины p. Таким образом, множество R(vi) получается путем последовательного выполнения слева направо операции объединения в выражении (9.1) до тех пор, пока мощность текущего множества не перестанет увеличиваться при очередной операции объединения. С этого момента последующие операции объединения не будут давать новых элементов множеству R(vi). Число объединений, которые необходимо выполнить, зависит от графа G. Но если граф конечен, то p < n (n – число вершин графа).

Определение 9.10. Матрицей достижимостей R {rij}n n называется

квадратная матрица порядка n, элементы которой rij определяются по формуле:

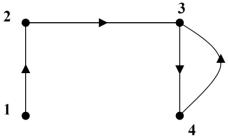
Пример 9.9. Построить матрицу достижимостей графа G, изображенного на рис. 9.9.

Рис. 9.9. Ор-граф

Решение. V = {v1, v2, v3, v4}, Г(v1) = {v2}, Г(v2) = {v3}, Г(v3) = {v4}, Г(v4) = {v3}.

R(v1) = {v1} {v2} {v3} v4} {v3} = {v1, v2, v3, v4}, R(v2) = {v2} {v3} {v4} {v3} = {v2, v3, v4},

R(v3) = {v3} {v4} {v3} = {v3, v4},

62

R(v4) = {v4} {v3} {v4} = {v3, v4}.

Следовательно, матрица достижимостей

Очевидно, что элементы rii = 1, i = 1, 2, , n, так как каждая вершина достижима из себя самой.

9.4. Операции над частями графа. Графы и бинарные отношения

Граф H = VH, EH называется частью графа G = V, E , если VH V,

EH E.

Если VH = V, то граф H называется суграфом. Суграф H является покрывающим для неориентированного графа G, если любая вершина графа G инцидентна хотя бы одному ребру из H.

Подграфом G’ графа G с множеством вершин V’ V называется часть, которой принадлежат все ребра с обоими концами из V’.

Над частями графа G можно выполнять следующие операции:

1. Дополнение H к части H – множество всех ребер графа G, не принадлежащих H:

E(H) E( H ) = , E(H) E( H ) = E(G).

2.Сумма (объединение) частей H1 и H2 графа G обозначается H1 H2

иопределяется как:

E(H1 H2) = E(H1) E(H2),

V(H1 H2) = V(H1) V(H2).

3. Произведение (пересечение) частей H1 и H2 графа G обозначается H1 H2 и определяется следующим образом:

E(H1 H2) = E(H1) E(H2),

V(H1 H2) = V(H1) V(H2).

Аналогично операциям над частями графа определяются операции над различными графами.

Пример 9.10. Для графов G1 и G2, изображенных на рис. 9.10, найти графы G1 G2 и G1 G2.

Решение. Находим объединение графов. Граф G1 G2 приведен на рис. 9.11. Пересечением графов G1 G2 является граф, изображенный на рис. 9.12.

63

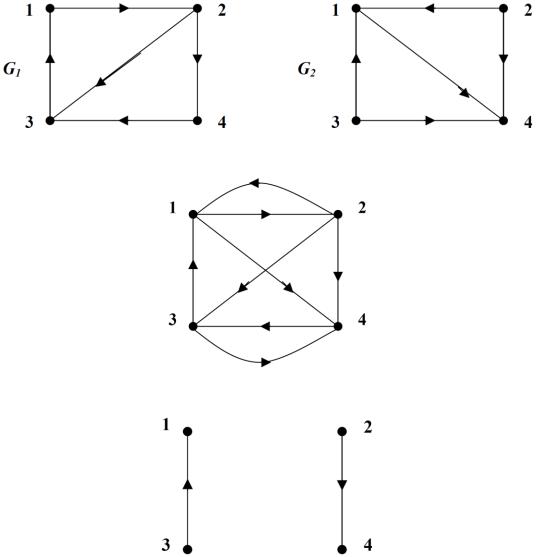
Рис. 9.10. Графы G1 и G2

Рис.9.11. Граф G1 G2

Рис.9.12. Граф G1 G2

Отношению R, заданному на множестве вершин графа V, взаимно однозначно соответствует ор-граф G(R) без кратных ребер с множеством вершин V, в котором ребро (v , v ) существует только в случае, если

выполнено v Rv .

9.5. Числа внутренней и внешней устойчивости графа

Определение 9.11. Рассмотрим граф G = G(V, Г(V)). Множество вершин называется внутренне устойчивым, если вершины попарно не смежны. Это означает, что любое множество S V, которое удовлетворяет условию S Г(S) = , является внутренне устойчивым множеством.

Внутренне устойчивое множество Si называется максимальным, если в G не существует другого такого внутренне устойчивого множества Sk, что

Si Sk.

64

Пример 9.11. Для графа, приведенного на рис. 9.13, множества

S1 = {v1, v3}, S2 = {v2, v4}, S3 = {v2, v6}, S4 = {v2, v4, v6}, S5 = {v2, v5} являются внутренне устойчивыми. Из них множества S1, S4 и S5 – максимальные, а

множества S2 и S3 не являются таковыми, так как S2 S4 и S3 S4.

Рис. 9.13. Неориентированный граф

Очевидно, что число элементов в разных максимальных внутренне устойчивых множествах не обязательно одинаковое.

Если Q – семейство всех внутренне устойчивых множеств графа G, то

число (G) max S называется числом внутренней устойчивости графа

S Q

G, а множество S*, на котором достигается этот максимум, называется

наибольшим независимым множеством.

Определение 9.12. Множество вершин T называется внешне устойчивым, если для любой вершины vi T Г (vi ) T .

Данное условие означает, что для каждой вершины vi T, существует дуга, идущая из некоторой вершины множества T в вершину vi.

Внешне устойчивое множество Ti называется минимальным, если в G не существует другого внешне устойчивого множества Tk, что Tk Ti.

Пример 9.12. Для графа, приведенного на рис. 9.14, множества

T1 = {v1, v4, v6}, T2 = {v1, v4}, T3 = {v3, v5, v6} являются внешне устойчивыми. Множества T2 и T3 – минимальные, а T1 не является минимальным, так как

внешне устойчивое множество T2 T1. В графе может быть несколько минимальных внешне устойчивых множеств и в общем случае они не содержат одинаковое число вершин.

Рис. 9.14. Ор-граф

65

Если P – семейство всех внешне устойчивых множеств графа G, то

число (G) min P называется числом внешней устойчивости графа, а

T P

множество T*, на котором достигается минимум, называется наименьшим внешне устойчивым множеством.

Пример 9.13. Найти число внутренней устойчивости графа (рис. 9.15).

Рис. 9.15. Ор-граф

Решение. Для заданного графа G = G(V, Г(V)) множество вершин

V = {v1, v2, v3, v4, v5, v6}, Г(v1) = {v2, v6}, Г(v2) = {v3}, Г(v3) = {v4}, Г(v4) = , Г(v5) = {v4, v6}, Г(v6) = {v4}.

Выбираем из множества V произвольную вершину vi1. Очевидно, что если граф не содержит петель, то множество {vi1}, состоящее из одной

внутренне устойчивым множеством: S2 Г(S2) = {v1, v3} {v2, v4, v6} = . Множество S2 – внутренне устойчиво.

vi3 = v5, поэтому S3 = {v1, v3, v5}. Множество S3 – максимальное внутренне устойчивое множество.

Для построения отличного от S3 максимального внутренне устойчивого множества в качестве исходной вершины выбираем вершину

S5 Г(S5) = {v1, v2} {v3, v2, v6} = {v2} , следовательно множество S5 не является внутренне устойчивым.

66

S8 Г(S8) = {v2, v4, v6} {v3, v4} = {v4} .

В результате данного построения получили новое максимальное внутренне устойчивое множество S6 = {v2, v4}.

Непосредственно проверкой можно убедиться в том, что множества

Глава 10. Маршруты в графах

10.1. Степени вершин графа

Определение 10.1. Пусть G – неориентированный граф. Если степени всех вершин графа конечны, то данный граф называется локально конечным. В частности, любой конечный граф локально конечен.

Пример 10.1. Для графа, изображенного на рис. 9.6, степени всех вершин графа равны: (1) = 2, (2) = 4, (3) = 4, (4) = 2, (5) = 5.

Если заданы матрицы инцидентности или смежности графа, то можно определить локальные степени всех его вершин.

Для матрицы инцидентности. В j-м столбце матрицы инцидентности, соответствующем вершине vj, единицы стоят на пересечении со строками, которым соответствуют инцидентные этой вершине ребра, а остальные элементы столбца равны 0. Необходимо также учесть, что петля дает вклад в степень вершины, равный 2. Следовательно,

67

дает вклад в степень вершины, равный 2. В результате для матрицы смежности имеем следующую формулу

n

(v j ) ij jj ,

i 1

где n – число вершин графа.

Для вершин ориентированного графа определяются две локальные степени:

1(v) – количество выходящих из вершины v ребер;2(v) – количество входящих в вершину v ребер.

Петля дает вклад в обе эти степени. Локальные степени вершин ориентированного графа можно выразить через коэффициенты его

Так как каждое ребро ор-графа G имеет одно начало и один конец, то

1 (v) 2 (v) m,

v G v G

где m – число ребер графа.

10.2. Маршруты, цепи и циклы

Определение 10.2. Пусть G – неориентированный граф. Маршрутом в графе G называется такая конечная или бесконечная последовательность ребер ( , e0, e1, , en, ), что каждые два соседних ребра ei–1 и ei имеют общую инцидентную вершину.

Одно и то же ребро может встречаться в маршруте несколько раз. Будем рассматривать в дальнейшем только конечные маршруты, т.е. конечные последовательности ребер (e1, , en). В таких маршрутах имеется первое ребро e1 и последнее ребро en. Вершина v0, инцидентная ребру e1 и не инцидентная ребру e2 называется началом маршрута. Аналогично определяется конец маршрута.

Вершины, инцидентные ребрам маршрута, кроме начальной и конечной, называются внутренними или промежуточными. Начало и конец маршрута могут одновременно оказаться и внутренней вершиной.

Пусть маршрут M = (e1, , en) имеет начало v0 и конец vm. Тогда его называют маршрутом, соединяющим вершины v0 и vm. Число ребер маршрута называется его длиной. Если v0 = vm, то маршрут называют циклическим. Отрезок (ei, , ei+j) маршрута M сам является маршрутом.

Он называется участком маршрута M.

Маршрут называется цепью, если каждое ребро встречается в нем не более одного раза, и простой цепью, если любая вершина графа инцидентна не более чес двум ребрам маршрута. Циклический маршрут

68

называют циклом, если он является цепью, и простым циклом, когда это простая цепь. Участок цепи или цикла является цепью, а участок простой цепи или простого цикла – простой цепью.

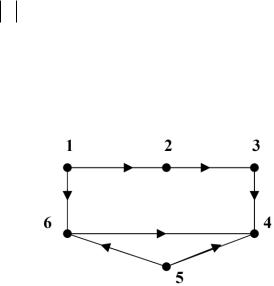
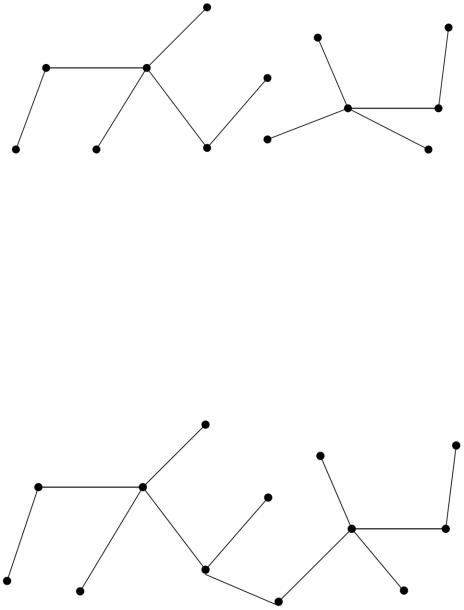
Неориентированный граф без циклов (а значит, без петель и кратных ребер) называется ациклическим графом, или лесом. Пример леса приведен на рис. 10.1.

Рис. 10.1. Ациклический граф

Вершины v , v G называются связанными, если существует маршрут с началом v и концом v . В этом случае существует также маршрут с началом v и концом v ; для этого ребра маршрута должны перечисляться в противоположном порядке.

Граф G называется связным, если все его вершины связаны между собой. Неориентированный связный граф без циклов называется деревом. Пример дерева приведен на рис. 10.2. Таким образом, компоненты связности леса являются деревьями, т.е. лес – дизъюнктное объединение деревьев.

Рис. 10.2. Граф без циклов

10.3. Расстояния в графе

Пусть G – связный неориентированный граф, v и v любые две его вершины. Тогда существует связывающая их простая цепь M = (e1, , ek). Если количество k ребер этой цепи не минимальное из возможных, то

69

существует цепь M (e1, , ek ) , связывающая v и v , и имеющая меньшее число ребер.

Определение 10.3. Минимальная длина простой цепи с началом v и концом v называется расстоянием d (v , v ) между этими вершинами.

Расстояние d (v , v ) удовлетворяет аксиомам метрики:

1)d(v , v ) 0 ;

2)d(v , v ) 0 тогда и только тогда, когда v v ;

3)d (v , v ) d (v , v ) .

4)Справедливо неравенство треугольника d(v ,v) d(v,v ) d(v ,v ) .

Пусть G – конечный связный неориентированный граф. Тогда можно

определить его диаметр как d (G) max d (v , v ) .

v ,v G

Кратчайшие простые цепи, связывающие вершины v , v G с максимальным расстоянием между ними, называются диаметрально простыми цепями.

Пусть v – произвольная вершина графа G. Максимальным удалением

от вершины v в графе G называется величина r(v) max d (v, v ) .

v G

Вершина v называется центром графа G, если максимальное удаление

от нее принимает минимальное значение r(G) min r(v).

v G

Максимальное удаление r(G) от центра называется радиусом графа, а любая кратчайшая цепь от центра v до максимально удаленной от него вершины v’ – радиальной цепью.

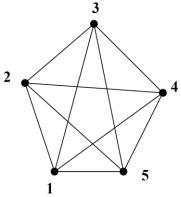
Центр не обязательно должен быть единственным. Например, в полном неориентированном графе G (любые две различные вершины такого графа соединены ребром) радиус равен 1 и любая вершина v G является центром (рис. 10.3).

Рис. 10.3. Полный неориентированный граф

70