
- •1. Общая теория статистики 4
- •Тема 1. Предмет, метод курса, этапы статистического исследования 4
- •Тема 3. Сводка и группировка материалов статистического наблюдения 25
- •Тема 6. Статистические показатели, методика их исчисления 55
- •Тема 7. Выборочное наблюдение 67
- •Тема 8 . Применение корреляционно-регрессионного анализа в статистике 69 введение
- •Вопрос № 2. Структура статистической науки
- •Вопрос № 3. Система органов государственной статистики. Задачи ведомственной статистики. Роль ее в современных условиях
- •Тема 2. Статистическое наблюдение План лекции
- •Вопрос № 1. Понятие статистического наблюдения
- •Вопрос № 2. Классификация статистического наблюдения по различным признакам
- •Вопрос № 4. Организационные вопросы статистического наблюдения
- •Вопрос № 6. Основные вопросы организации статистической отчетности
- •Тема 3. Сводка и группировка материалов статистического наблюдения
- •Вопрос 1. Понятие о статистической сводке, ее задачи и содержание
- •Вопрос 2 Методические вопросы статистических группировок, их значение в экономическом исследовании
- •Тема 4. Рациональные формы изложения статистического материала План лекции
- •Вопрос № 1. Статистическая таблица и ее элементы
- •Основные правила построения таблиц
- •Основные элементы статистических графиков
- •Классификация статистических графиков
- •Дни недели
- •Вопросы для самопроверки
- •Тема 5. Абсолютные и относительные статистические величины План лекции
- •Вопрос № 1. Статистические величины. Их классификация
- •Вопрос № 2. Абсолютные величины, их основные виды
- •Вопрос № 3. Относительные величины, их значение и основные виды
- •Тема 6. Статистические показатели, методика их исчисления
- •Тема 7. Выборочное наблюдение
- •Тема 8 . Применение корреляционно-регрессионного анализа в статистике
Тема 8 . Применение корреляционно-регрессионного анализа в статистике
Изучаемые вопросы
1. Определение формы корреляционной зависимости.
2. Расчет параметров уравнения репрессии и тесноты связи.
1. Любое общественное явление находится в связи с другими явлениями; исследование таких взаимосвязей - важнейшая задача статистики. Наиболее часто для этого используют метод корреляции. Термин корреляции происходит от английского слова correlation - соотношение, соответствие. К изучению связи методом корреляции обращаются в том случае, когда нельзя игнорировать влияние посторонних факторов. При этом число наблюдений должно быть достаточно велико, так как малое число наблюдений не позволяет обнаружить закономерность связи.
Первая задача корреляции заключается в выявлении на основе значительного числа наблюдений того, как меняется в среднем результативный признак в связи с изменением одного или нескольких факторов. Вторая задача состоит в определении степени влияния искажающих факторов. Первая задача решается определением уравнения регрессии и носит название регрессионного анализа. Вторая - определением различных показателей тесноты связи и называется собственно и корреляционным анализом.
При изучении влияния одних признаков явлений на другие из цепи признаков, характеризующих данное явление, выделяются факторные и результативные признаки. Выделение признаков ведется логическим анализом.
Например, производительность труда зависит от стажа работы, разряда рабочих. Значит, производительность труда – результативный (функциональный) признак, а стаж, разряд рабочего - факторный признак (аргумент).
Связь между двумя взаимосвязанными признаками легко изобразить графически. Для этого результативный признак (функцию) обозначают y, а факторный (аргумент) - x.
Пару чисел легко представить на плоскости, образуемой системой прямоугольных координат, при этом факторный признак откладывается на оси абсцисс и результативный - на оси ординат.
Если одному значению факторного признака соответствует только одно значение результативного, то такая связь называется функциональной. Функциональные связи легко представить формулами. Например, зависимость силы тока от величины напряжения к сопротивлению в электрической цепи (закон Ома).
Связь между случайными величинами называется стохастической. Эта связь характеризуется тем, что результативный признак не полностью определяется факторным признаком, его влияние проявляется в среднем при достаточно большом числе наблюдений.
Пример
Имеются следующие данные о разряде рабочего и среднемесячной заработной плате.
Разряд |
1 |
1 |
2 |
2 |
2 |
2 |
3 |
3 |
3 |
3 |
3 |
Среднемесячная з/п, р. |
100 |
120 |
150 |
160 |
170 |
190 |
180 |
180 |
180 |
190 |
200 |
Разряд |
4 |
4 |
4 |
4 |
4 |
5 |
5 |
6 |
6 |
6 |
|
Среднемесячная з/п, р. |
180 |
240 |
250 |
300 |
300 |
280 |
280 |
340 |
360 |
410 |
|
Изобразим эти данный графически (рис. 7).
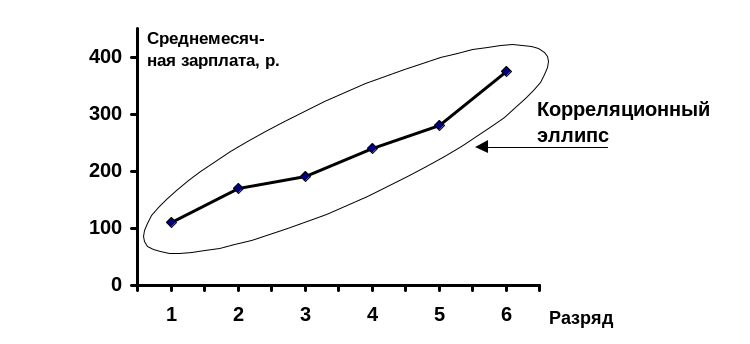

Рис. 7. График корреляционной зависимости (поле корреляции)
Видно, что одному значению аргумента (разряду) соответствует ряд распределения функции (зарплаты). Ряды распределения функции закономерно смещаются - зарплата в среднем увеличивается с повышением разряда. Найдем средние значения аргумента и функции.
|
1 |
2 |
3 |
4 |
5 |
6 |
|
110 |
168 |
186 |
254 |
280 |
370 |
![]()
![]() и т.п.
и т.п.
Нанесем на график и и соединим ломаной линией (рис. 7).
Эта
линия изображает взаимосвязь между
средними значениями аргумента и функции
и называется эмпирической
линией регрессии.
Необходимо установить теоретическую
линию регрессии,
т.е. установить функцию, связывающую
результативный и факторный признаки.
Полученная ломаная регрессия (рис. 8)
может помочь в выборе функции. Увеличение
или уменьшение результативного и
факторного признаков в арифметической
прогрессии означают, что сглаживание
нужно производить по прямой
![]() .
В этом случае эмпирические графики
должны быть (рис. 8):
.
В этом случае эмпирические графики
должны быть (рис. 8):
Если
равноускоренное или равнозамедленное
изменение функции (рис. 9), то сглаживание
можно провести по параболе второго
порядка
![]() или по гиперболе
или по гиперболе
![]() .
.
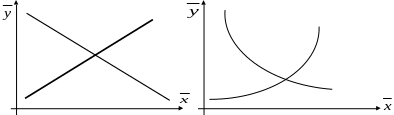
Рис. 8 . Эмпирические линии регрессии Рис. 9. Эмпирические линии регрессии при
при зависимости по прямой зависимости по параболе и гиперболе
Более сложные зависимости могут быть иллюстрированы параболой третьего порядка, логарифмической или показательной функцией.
2. Выбрав теоретическую функцию, описывающую корреляционную зависимость между результативным и факторным признаком, нужно рассчитать параметры уравнения регрессии. Расчет чаще всего производится по способу наименьших квадратов при использовании системы нормальных уравнений.
Эти системы различны для разного рода кривых:
Прямая линия ;
![]() (38)
(38)
Парабола второго порядка ;
![]() (39)
(39)
Гипербола .
![]() . (40)
. (40)
В
нашем примере, используя в качестве
теоретической функции прямую
![]() ,
рассчитаем параметры уравнения по (38).
,
рассчитаем параметры уравнения по (38).
Для
этого определим
![]() .
.
Решив систему нормальных уравнений, найдем a 54, b 50.
Следовательно,
уравнение имеет вид
![]() .
.
Значит,
для рабочего 2 разряда зарплата по
уравнению рассчитывается
![]() (р.)
- что отличается от эмпирических данных.
(р.)
- что отличается от эмпирических данных.
Теснота или сила связи между двумя признаками может быть измерена эмпирическим корреляционным отношением ()
![]() . (41)
. (41)
В случае прямолинейной связи тесноту можно определить с помощью коэффициента корреляции (r).
![]() . (42)
. (42)
Коэффициент корреляции может изменяться от +1 до -1. Чем ближе значение r по абсолютной величине к единице, тем теснее связь. Если r > 0, то связь между факторным и результативным признаком прямо пропорциональная, если r < 0, то - обратно пропорциональная.
В нашем примере:
по
(42) ![]()
Значит, связь прямо пропорциональная, достаточно тесная.
Используя
найденное теоретическое уравнение
корреляции, можно найти неизвестное
значение
![]() ,
зная x.
,
зная x.
Вопросы для самопроверки
Как рассчитать и построить эмпирическую линию регрессии?
Постройте теоретическую линию регрессии, если r = -0,8.
Чем теоретическая линия регрессии отличается от эмпирической?
