Тема 7. Выборочное наблюдение
Изучаемые вопросы
Способы формирования выборочной совокупности.
Определение ошибок выборочной совокупности.
Определение численности выборки.
1. Наблюдение не всегда охватывает все единицы совокупности, иногда в силу большой стоимости или при контроле качества, когда проверка сопровождается разрушением образцов, невозможно провести наблюдение над всей совокупностью.
В этом случае проводят выборочное наблюдение, при котором обследованию подвергается часть единиц совокупности, отобранных случайно, но с заранее известной численностью.
Вся
совокупность, из которой производится
отбор, называется генеральной,
а совокупность отобранных единиц -
выборочной.
В процессе обследования выборочной
совокупности можно рассчитать среднее
значение исследуемого признака по
выборке (
),
которое будет отличаться от аналогичной
средней по генеральной совокупности
(
):
,
т.к. обследование было не сплошным.
Величина, на которую отличается
от
,
является ошибкой выборки (репрезентативности).
Чем блике размер выборочной совокупности
к генеральной, тем меньше ошибка
репрезентативности.
Выборочная совокупность может формироваться разными методами. Может быть индивидуальный отбор (когда отбирается каждый раз одна единица совокупности) или серийный.
После отбора отобранные единицы могут быть возвращены в генеральную совокупность - повторный отбор, либо могут не участвовать в дальнейшем отборе - бесповоротный отбор.
Отбор может быть произведен: собственно-случайным способом, механическим, типическим и серийным способами.
При собственно-случайной выборке отбор производится обычной жеребьевкой. Собственно-случайная выборка в статистической практике применяется редко. Обычно отбор осуществляется механически - через определенный интервал. Например, отбор каждого 5-го, 10-го и т.д. студента по алфавитному списку фамилий.
При типическом отборе обследуемая генеральная совокупность подразделяется на типические группы, из которых затем отбирается определенное число единиц так, чтобы сохранить в выборке структуру генеральной совокупности.
При серийной выборке отбор проводится не отдельных единиц, а серий или комплектов.
2. Как уже было сказано выше, между характеристиками выборочной и генеральной совокупности есть разница - ошибка репрезентативности. Ошибки репрезентативности могут быть рассчитаны как средняя и с определенной вероятностью – предельная ошибка.
Средняя ошибка выборки () рассчитывается:
при
повторном отборе
,
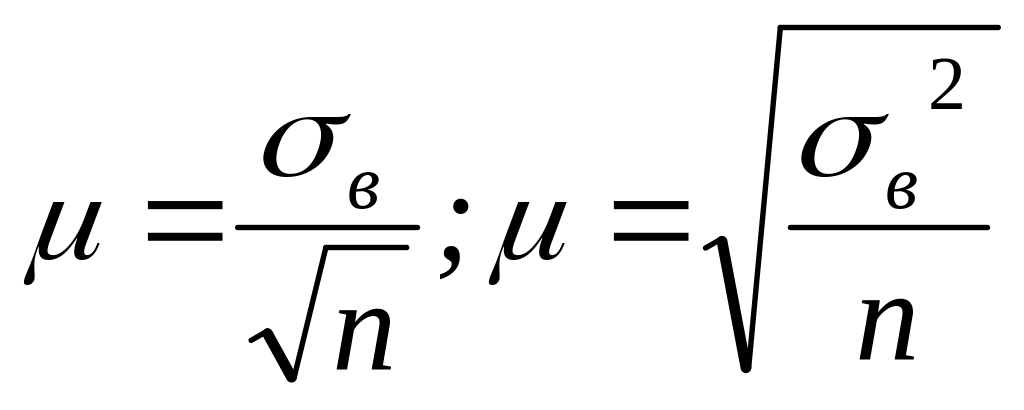(34)
при
бесповторном отборе
,
(35)
где – среднее квадратическое отклонение; n - численность выборочной совокупности; N - численность генеральной совокупности.
Если
выборочное наблюдение применяется для
определения доли признака, то в формулах
вместо среднего квадратического
отклонения ставят
(см. тема 2, вопрос 3).
Пример. При разработке материалов учета городского населения методом случайного бесповторного отбора было установлено, что в городе 15% жителей - пенсионеры. При этом из 500 тыс. жителей было отобрано 50 тыс. Определить среднюю ошибку для доли жителей-пенсионеров в генеральной совокупности.
По
(35)
Значит в среднем ошибка 4,8%.
Предельная ошибка выборки () связана со средней коэффициентом доверия (t): = t .
Коэффициент доверия зависит от вероятности, с которой можно гарантировать определенные размеры предельной ошибки:
Коэффициент доверия (t) |
Вероятность |
1 |
0,683 |
2 |
0,954 |
3 |
0,997 |
Чтобы
определить значение признака в генеральной
совокупности (
),
нужно скорректировать его значение по
выборке на предельную ошибку выборки
():
Продолжив
наш пример, найдем предельную ошибку
для доли пенсионеров с вероятностью
0,954. В этом случае t
= 2, то есть
= 2
0,048 = 0,096. Значит, доля по генеральной
совокупности ()
будет отличаться от доли по выборке
()
на 9,6%:
.
Т.е. доля пенсионеров в городе находится
в пределах от 24,6 до 5,4%.
3. Приведенные выше формулы ошибок выборки позволяют заранее рассчитать тот объем выборки, при котором отклонение выборочных показателей от генеральных не превысит заданных размеров, гарантируемых с определенной вероятностью.
Численность выборки (n):
при
повторном отборе
; (96)
при
бесповторном отборе
.
(97)
Пример. В городе проживает 2000 семей. В порядке случайной бесповоротной выборки предполагается определить средний размер семы при условии, что ошибка выборочной средней не должна превышать 0,8 с вероятностью 0,954 и при среднем квадратическом отклонении 2,0:
По
(97) 
При определении необходимой численности выборки по этим формулам для определения дисперсий используют данные предыдущих обследований. При полном отсутствии каких-либо данных о вариации альтернативного признака вместо pq подставляют его максимальное значение, равное 0,25.
Выборочное обследование широко используется в статистических исследованиях при контроле качества, обследованиях бюджетов семей, изучении резервов в производстве.
Вопросы для самопроверки
Может ли средняя ошибка выборки равняться предельной?
При каком способе отбора ошибка репрезентативности меньше?
От каких параметров зависит численность выборочной совокупности?