2.1. Спектральные свойства широкополосных фм сигналов
Спектральные свойства ФМ сигнала определяются спектром одиночного импульса U0(t) и КП А.
Спектр одиночного
импульса
определяется спектральной плотностью
амплитуд (СПА)
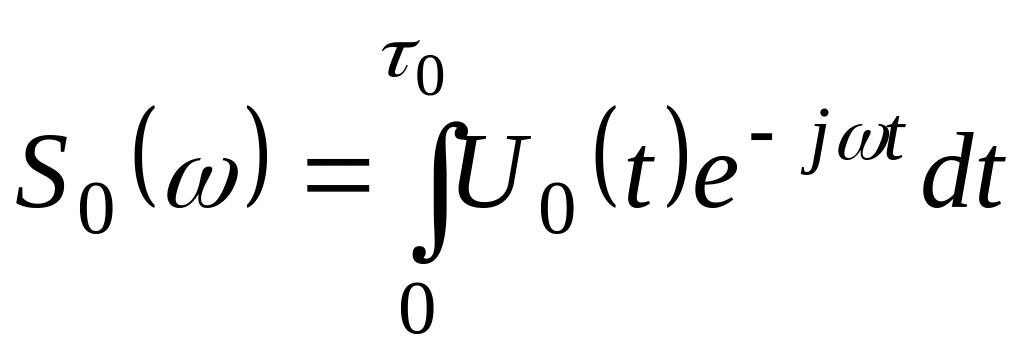. (2.2)
Для прямоугольного импульса единичной амплитуды СПА равна
.
(2.3)
состоит из трех
сомножителей:
первый - площадь
импульса, равная
;
второй - имеет вид функции отсчета
и характеризует распределение СПА по
частоте;
третий -
определяет фазовый сдвиг, который,
согласно теореме запаздывания, является
следствием смещения на
центра импульса
относительно начала координат.
В результате СПА огибающей ФМ сигнала (2.1) имеет вид (теорема лин.)
,
(2.4)
которую можно представить в виде:
, (2.5)
где
-
спектр КП.
Для бинарного ФМ
сигнала символы an
являются действительными величинами
±1. Поэтому модуль амплитудного спектра
КП
является четной функцией частоты, а
фазовый спектр
-
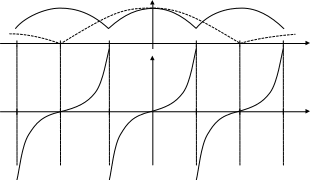
нечетной (Рис.2.1):
, (2.6)
.
(2.7)
0
0
Рис 2.1. Амплитудный и фазовый спектры огибающей ФМ-2 сигналов.
Т. к.
,
то при
-
равен среднему значению амплитуд
(разбалансированности) КП и амплитуда
флуктуирует со средней частотой ωср=2π/
τ0
согласно косинусному множителю, а
среднее значение квадрата модуля
амплитудного спектра КП ( мощность
)
равно
.
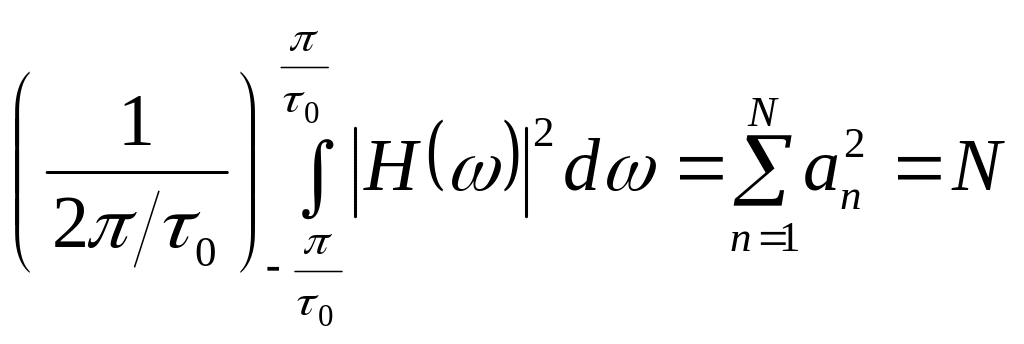(2.8)
Поэтому для кодовой
последовательности реальных ФМ сигналов
флуктуации
происходит около среднего значения
,
а для сигналов с АКФ без боковых пиков
(идеальной) этих флуктуаций не будет
ид
=
.
(2.9)
2.2.Свойства корреляционных функций фм сигналов
Свойства корреляционных функций (КФ) важны при оптимальном приеме сигналов коррелятором или СФ, нормированный отклик которого
(2.10)
определяет КФ (связь между сигналами uj(t), uk(t) ) при сдвиге τ.
Общей характеристикой корреляционных свойств двух сигналов при сдвиге τ ≠ 0 и доплеровском смещении частоты сигнала Ω ≠ 0 является нормированная взаимная функция неопределенности (ВФН) Rjk(τ,Ω):
,
(2.11)
которая определена комплексными огибающими или спектрами сигналов.
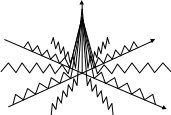
Функция неопределенности (ФН) R(τ,Ω) равна ВФН при j=k (прием на СФ [П]) и имеет вид, например, рис.2.2 для ПСП (2.1) из N импульсов.
1,0
-T
0
4π/T
2τ0
-
=
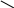-2πF
T
Рис. 2.2. Тело ФН (т.е. ВФН при j=k) для =N∙τ0 =Т, F=N/ Т.
Взаимная корреляционная функция (ВКФ) Rjk(τ) равна ВФН при Ω=0.
Нормированный отклик СФ при любых j и k определен через ВФН
, (2.12)
а объем тела нормированной ВФН равен единице:
(2.13)
Полагая при j ≠ k тело параллелепипедом, объем (интеграл) которого определен на прямоугольнике со сторонами 2T и 2Ω = 2∙2πF, и высотой эффективного значения Rjkэф ВФН, найдем Rjkэф из равенства: R2jkэф∙4F T=1, откуда нижняя граница оценки взаимных боковых пиков двух ШПС равна
. (2.14)
Автокорреляционная функция (АКФ) R (τ) равна сечению ФН при Ω=0.
Частотная
корреляционная функция
(ЧКФ) R(Ω)
определена
сечением ФН при τ
=0 и является
преобразованием Фурье (2.11) от
ШПС, не зависит от ФМ сигнала и для
прямоугольного импульса (рис.1.3б)
длительностью Т
равна:
. (2.15)
Ширина лепестка по первым нулям равна 4π/Т и определяет разрешение по доплеровской частоте и погрешность σf..
ВФН (2.11) для апериодического ФМ ШПС (2.1) имеет вид
., (2.16)
где
,
-
символы кодовых последовательностей
и
,
причем
* - знак комплексной сопряженности для случая многофазных сигналов;
R0(τ,Ω)
– ФН единичного
импульса, которая при
равна
(2.17)
При
и
ВКФ ФМ сигналов определяется соотношением:
,
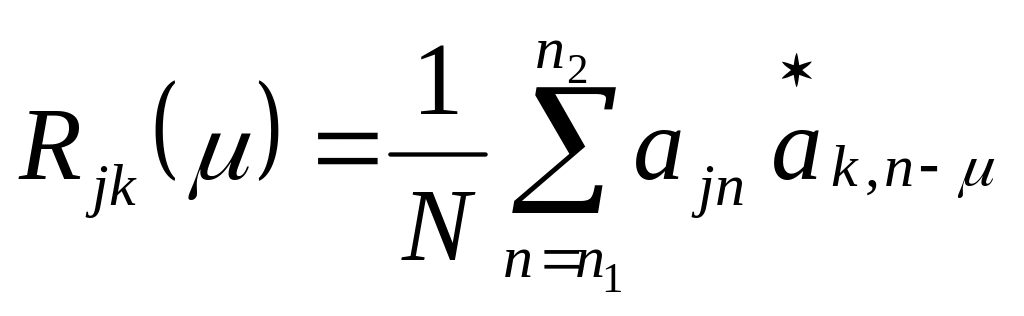(2.18)
где 
,
откуда при
имеем АКФ, которая с учетом четности
,
равна:
(2.19)
Можно показать,
что ВКФ и АКФ периодического
ФМ ШПС определяется также выражениями
(2.18) и (2.19), где n=1,
а
.
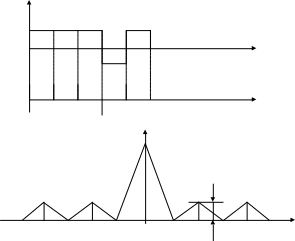
На рис.2.3а представлена
действительная огибающая (2.1) бинарного
апериодического ФМ сигнала Баркера
при N=5
с вещественными амплитудами импульсов
(рис.(2.3б), а на рис.2.3в АКФ согласно
(2.19), где
.
U(t)
а)
t
0 Т
б)
t
в) 1
;
1/5
-4 -2 0 2 4 μ=τ/ τ0
Рис.2.3. Огибающая бинарного ФМ сигнала и его АКФ.
В Приложении и [3, раздел 3] представлен пример реализации СФ и выходная АКФ для сигнала Баркера при N=7.
Между КФ и спектрами Н(ω) кодовых последовательностей А существует взаимосвязь. Для ВФН справедливо интегральное равенство
,
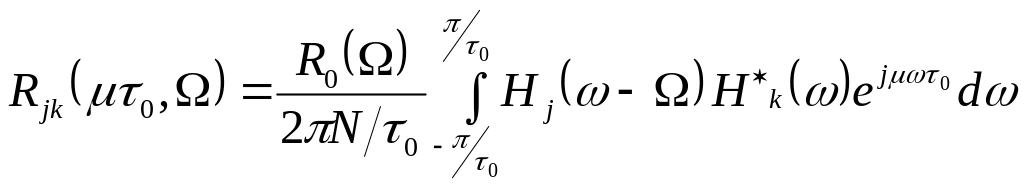(2.20)
которое используется при нахождении оценок ВКФ и АКФ.
При , из (2.20) следует нормированная АКФ:
.
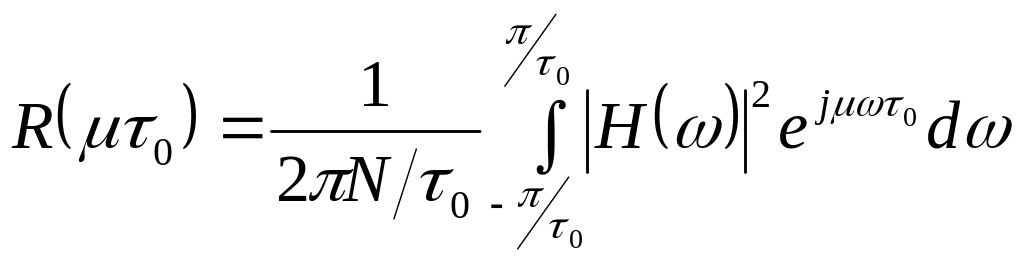(2.21)
При
из (2.21) после умножения на N
следует (2.8), т.е. мощность
=
R
(0) ПСП.