Задача о рюкзаке

В общем виде задача о рюкзаке формулируется следующим образом. Имеется рюкзак определенного объема W_max и неограниченное количество предметов. Для каждого предмета известен его вес (объем) W_i и полезность (ценность, стоимость) P_i. В рюкзак можно положить целое число предметов различного типа.

Цель: собрать такой набор предметов, чтобы общая полезность P всех находящихся в рюкзаке предметов была наибольшей, а суммарный вес не превышал заданной величины W_max.

К подобной формулировке может быть сведена задача максимального использования грузоподъемности подвижного состава, грузовместимости судна, автомобиля и т.п. Такая задача часто возникает при выборе оптимального управления в экономико-финансовых областях (например, распределение бюджета отдела по проектам).

Рассмотрим задачу о рюкзаке на конкретном примере.

Пример 4. Имеется рюкзак весом W_max = 200 кг и предметы 3-х типов. Вес W_i и полезность P_i одного предмета каждого типа составляет соответственно 20 кг и 210 баллов, 12 кг и 130 баллов, 16 кг и 170 баллов. Требуется "упаковать" рюкзак так, чтобы общая полезность P упакованных предметов была наибольшей и их общий вес не превышал 200 кг.

Решение.

1. Разработка математической модели.

Введем обозначения:

x₁ – необходимое количество предметов 1-го типа;

x₂ – необходимое количество предметов 2-го типа;

x₃ – необходимое количество предметов 3-го типа.

Запишем целевую функцию в виде:

f(x₁, x₂, x₃) = 210x₁ + 130x₂ + 170x₃  → max

20x₁ + 12x₂ + 16x₃ <= 200 – ограничение по весу;

x₁, x₂, x₃ – целые значения.

2. Формализация модели в Excel.

На рабочем листе Excel подготовим исходные данные, как показано на рис. 6. Для аргументов целевой функции x₁, x₂, x₃, x₄ выделим ячейки D7:D10. Для предметов каждого типа в ячейки E7:E10 (рис. 9) введем формулы для расчета общего веса, в ячейки F7:F10 – формулы для расчета общей полезности. В ячейку F11 введем формулу целевой функции, в ячейку E11 – формулу ограничения.

а	б
Рис. 9. Вид рабочего листа Excel для примера 4 (а – обычный режим просмотра, б – режим показа формул)

Задача состоит в том, чтобы за счет подбора значений ячеек D7:D10 добиться максимального значения целевой ячейки F11.

3. Настройка инструментов Поиск решения.

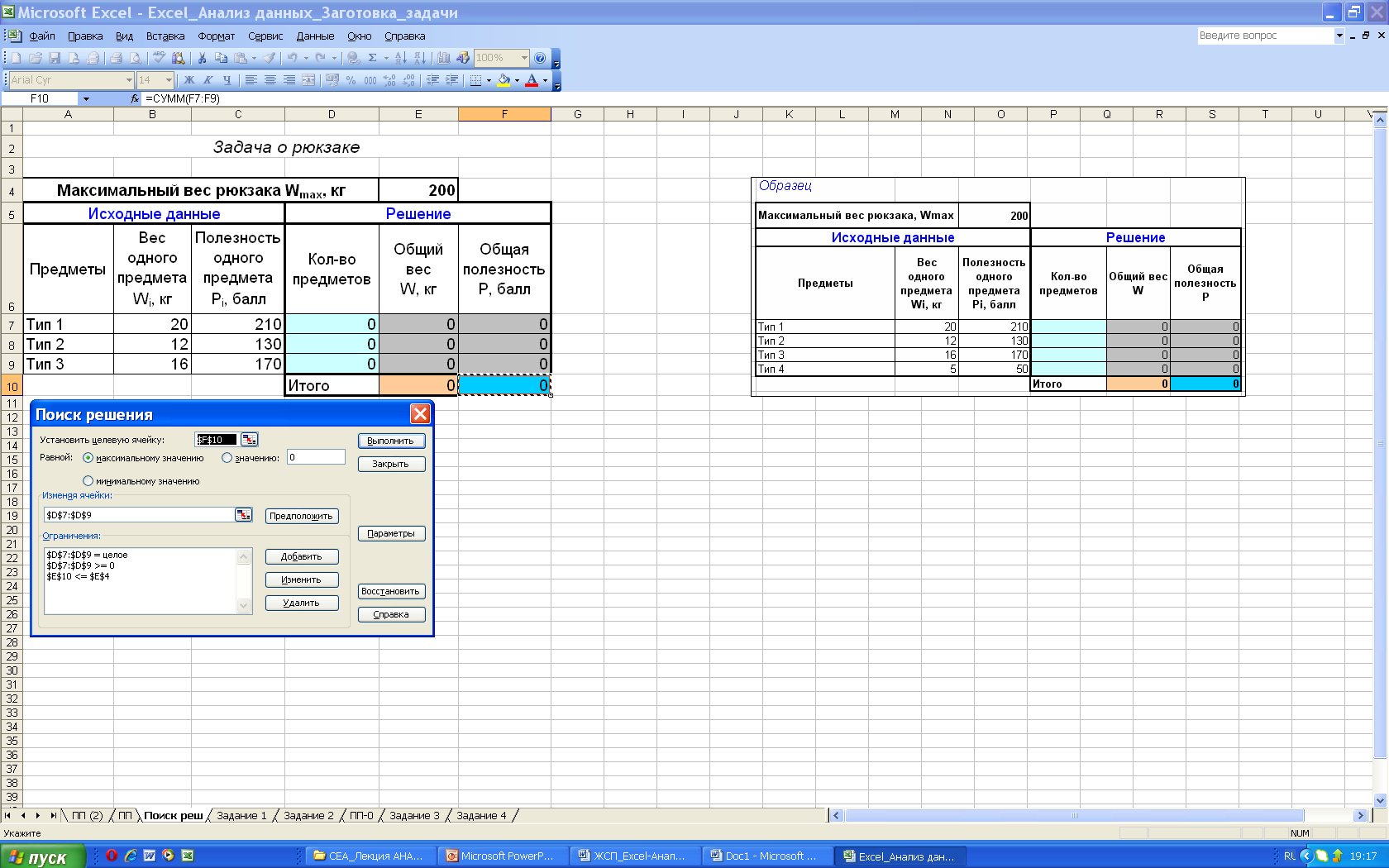
Выполним команду меню Сервис→Поиск решения – откроется диалоговое окно Поиск решения. Укажем в диалоговом окне (рис. 10):

– ссылку на целевую ячейку F11;

– ссылки на изменяемые ячейки D7:D10, в которых размещены параметры целевой функции;

– по кнопке Добавить введем все ограничения.

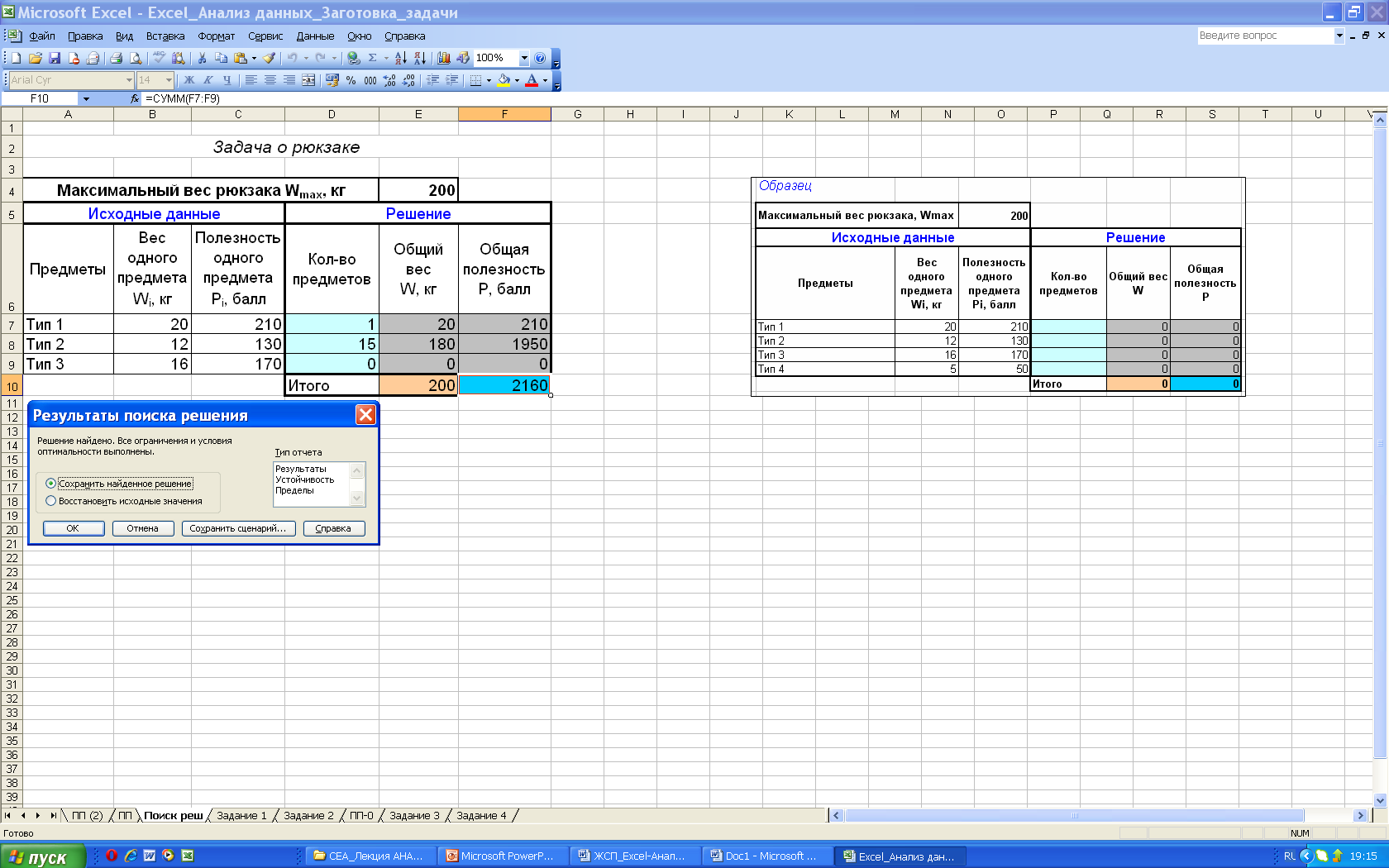
Рис. 10. Диалоговое окно Поиск решения	Рис. 11. Окно Результаты поиска решения

После щелчка на кнопке OK в ячейках D7:D10 будет получено решение – значения x₁, x₂, x₃, при которых целевая функция имеет максимальное значение при заданных ограничениях (рис. 11).

Таким образом, из предложенных предметов, имеющих наибольшую полезность и не превышающих допустимого веса 200 кг, в рюкзак имеет смысл положить один предмет 1-го типа и 15 предметов 2-го типа.

Одним из дополнительных ограничений при практическом использовании данной задачи могут быть ограничения на необходимое количество предметов определенного типа, которые можно положить в рюкзак. При этом возможны варианты, когда требуется:

– строго определенное количество предметов;

– не менее (не более) заданного количества предметов.