Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

"Московский государственный технический

университет радиотехники, электроники и автоматики"

Подлежит возврату

№ 0000

ИСПОЛЬЗОВАНИЕ MATLAB В МЕДИКО-БИОЛОГИЧЕСКИХ СИСТЕМАХ

Методические указания

по выполнению лабораторных работ

Для студентов, обучающихся по направлению подготовки специалистов 201000 «Биотехнические системы и технологии».

МОСКВА 2012

Составитель: А.И. Михальский

Редактор: Н.А. Бабушкина

Методические указания содержат рекомендации по проведению лабораторных работ по курсу «Использование MATLAB в медико-биологических системах» и включают в себя описания трёх лабораторных работ с контрольными вопросами для самопроверки.

Предназначены для студентов всех форм обучения по направлению подготовки специалистов 201000 «Биотехнические системы и технологии», а также могут быть полезны для студентов, обучающихся по другим направлениям и специальностям

Печатается по решению редакционно-издательского совета университета.

Рецензенты: В.Н. Новосельцев

А.Я. Червоненкис

© МГТУ МИРЭА, 2012

Введение

Лабораторные работы по курсу «Использование MATLAB в медико-биологических системах» предназначены для закрепления полученных теоретических знаний и приобретения навыков работы в среде MATLAB с использованием её вычислительных, симуляционных, графических возможностей. Настоящий лабораторный практикум включает описания трёх лабораторных работ по изучению основных свойств распределений случайных величин и их оценок, по изучению характеристик и графическому представлению распределения длительности событий с использованием модели Гомпертца-Мейкхема, по исследованию точности оценок параметров модели распределения длительности события, построенных методом максимального правдоподобия. При выполнении лабораторных работ студенты осваивают основы работы в системе MATLAB, операторы генерации случайных чисел и векторов, принципы построения 2D и 3D графиков в MATLAB, элементы математической статистики.

Перед выполнением лабораторной работы студент должен изучить основные теоретические положения, методику выполнения работы и пройти инструктаж по технике безопасности. Рабочим местом для выполнения лабораторных работ является персональный компьютер, где установлена версия MATLAB 7 и выше.

В процессе выполнения лабораторной работы студент формирует отчёт в редакторе MS Word, в котором должны быть персональные данные студента, название и цель работы, необходимые блок-схемы алгоритма выполнения работы, расчёты, листинги программ и результаты вычислений в виде таблиц, графиков, а также выводы по результатам проделанной работы. Утверждённый преподавателем отчёт следует сохранить на внешнем носителе (флешка). В печатном виде на стандартных листах белой бумаги формата А4 отчёт служит основой для беседы при зачёте.

Задания для выполнения лабораторных работ Лабораторная работа № 1 «Знакомство с matlab, изучение основных свойств случайных величин и их оценок»

Цель работы:

• Знакомство с основными матричными операциями в MATLAB и операторами построения 2D графиков.

• Освоение операций генерирования случайных чисел с различными законами распределения.

• Построение оценок математического ожидания и дисперсии по независимым выборкам значений случайных величин.

Задание для домашней подготовки:

1. Ознакомиться с принципами работы в системе MATLAB [1], с.13 -38.

2. Изучить основные операторы MATLAB, операторы построения 2D графиков [1], с.39 -55.

3. Ознакомиться с процедурами MATLAB для генерирования равномерно, экспоненциально, нормально распределённых случайных величин [2], с.218 -221.

4. Ознакомиться с формулами для оценки математического ожидания и дисперсии по независимым выборкам значений случайных величин [3], с.197-207.

Порядок выполнения лабораторной работы.

• Вызвать MATLAB.

• Открыть новый файл для редактирования, записав в первой комментарий:

% программа выполнения лабораторной работы № 1

% работу выполнил студент ….. группы ….. задание ....

Операторы, реализующие выполнение задания по лабораторной работе должны заноситься в этот файл.

• Сохранить файл под именем Lab1.m

Задание 1. Генерирование выборки случайных величин, имеющих равномерное распределение

Случайная величина, имеющая равномерное на отрезке [a,b] распределение, описывается плотностью вероятности вида

.

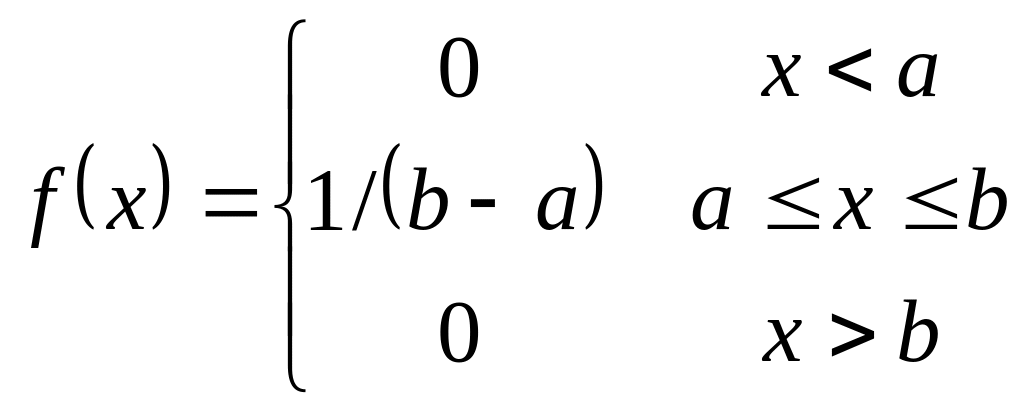Математическое ожидание такой случайной величины равно

, (1.1)

а её дисперсия равна

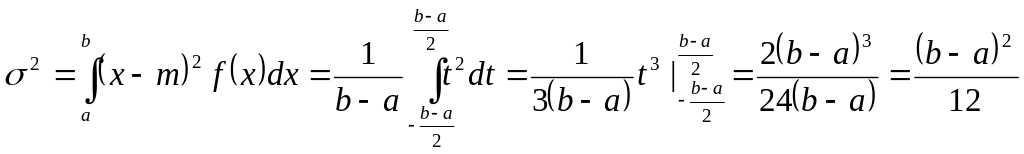. (1.2)

Оценка величины математического ожидания случайной величины, вычисленная по независимой выборке , задаётся формулой

, (1.3)

оценка дисперсии случайной величины, вычисленная по независимой выборке , равна

. (1.4)

1. Получите у преподавателя значения параметров a, b и n. Запишите оператор для генерации независимой выборки значений равномерно распределённой случайной величины с выданными параметрами

X=rand(1,n)*(b-a)+a;

2. Графически отобразите сгенерированную выборку с помощью оператора

plot(X);

3. Вычислите точные значения математического ожидания и дисперсии случайной величины, вычисленные по формулам (1.1) и (1.2). Сравните эти величины с их оценками, вычисленными по формулам (1.3) и (1.4). Для выполнения этого пункта запишите следующие операторы Matlab

m=(b+a)/2; s2=(b-a)^2/12;

mh=sum(X)/n; sh2=sum((X-m).^2)/(n-1);

disp([‘Given mean=’,num2str(m),’ variance=’,num2str(s2)]);

disp([‘Estimated mean=’,num2str(mh),’ variance=’,num2str(sh2)]);

4. С помощью команды run Lab1 выполните записанные операторы. Значения параметров, построенный график и выведенные на экран числа внесите в отчёт о выполнении лабораторной работы. Сделайте вывод о близости значений математического ожидания и дисперсии случайной величины, вычисленных по формулам (1.1) и (1.2) и их оценок, вычисленных по формулам (1.3) и (1.4).

Задание 2. Генерирование выборки случайных величин, имеющих экспоненциальное распределение

Случайная величина, имеющая экспоненциальное распределение, описывается плотностью вероятности вида

.

Математическое ожидание такой случайной величины равно

, (2.1)

а её дисперсия равна

. (2.2)

Оценка величины математического ожидания случайной величины, вычисленная по независимой выборке , задаётся формулой

, (2.3)

оценка дисперсии случайной величины, вычисленная по независимой выборке , равна

. (2.4)

1. Получите у преподавателя значения параметров a и n. Запишите оператор для генерации независимой выборки значений равномерно распределённой случайной величины с выданными параметрами

X=exprand(1/a,n);

2. Построить гистограмму распределения сгенерированной выборки с помощью оператора

hist(X);

3. Вычислите точные значения математического ожидания и дисперсии случайной величины, вычисленные по формулам (2.1) и (2.2). Сравните эти величины с их оценками, вычисленными по формулам (2.3) и (2.4). Для выполнения этого пункта запишите следующие операторы Matlab

m=1/ a; s2=1/a^2;

mh=sum(X)/n; sh2=sum((X-m).^2)/(n-1);

disp([‘Given mean=’,num2str(m),’ variance=’,num2str(s2)]);

disp([‘Estimated mean=’,num2str(mh),’ variance=’,num2str(sh2)]);

4. С помощью команды run Lab1 выполните записанные операторы. Значения параметров, построенный график и выведенные на экран числа внесите в отчёт о выполнении лабораторной работы. Сделайте вывод о близости значений математического ожидания и дисперсии случайной величины, вычисленных по формулам (2.1) и (2.2) и их оценок, вычисленных по формулам (2.3) и (2.4).

Задание 3. Генерирование выборок двух случайных величин, имеющих совместное нормальное распределение

Две случайные величины t и z, имеющие совместное нормальное распределение, описывается плотностью вероятности вида

.

Параметры и являются математическими ожиданиями случайных величин t и z соответственно. Матрица К - ковариационная матрица, составлена из дисперсий и ковариаций t и z

.

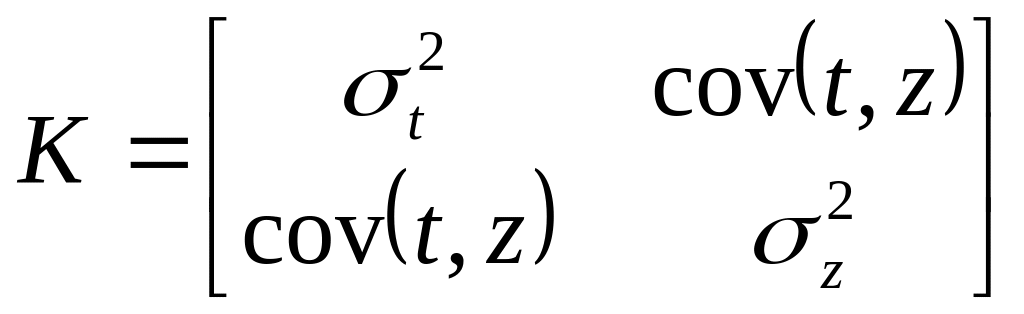Оценка величин математических ожиданий случайных величин, вычисленная по независимой выборке пар значений , задаётся формулами

, . (2.1)

Элементы ковариационной матрицы оцениваются по формулам

, , .(2.2)

1. Получите у преподавателя значения параметров 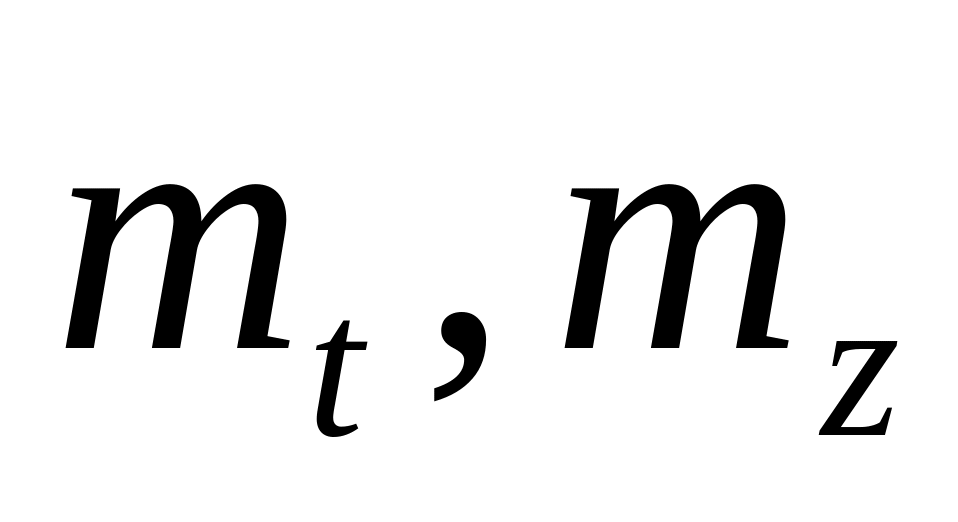, ковариационной матрицы К и n. Запишите оператор для генерации независимой выборки пар значений случайных величин t и z, имеющих совместное нормальное распределение с заданными параметрами

X=mvnrnd([mt,mz],K,n);

2. Постройте представление распределения сгенерированных величин с помощью расположенных на плоскости звёздочек, записав оператор

plot(X(:,1),X(:,2),’*’);

xlabel(‘t’); ylabel(‘z’)

3. Вычислите оценки математических ожиданий случайных величин t и z по формулам (2.1) и оценки элементов ковариационной матрицы по формулам (2.2). Сравните эти величины с заданными в задании параметрами. Для выполнения этого пункта запишите следующие операторы Matlab

mth=sum(X(:,1))/n;

mzh=sum(X(:,2))/n;

st2=sum((X(:,1)-mth).^2)/(n-1);

sz2=sum((X(:,2)-mzh).^2)/(n-1);

cv=sum((X(:,1)-mth) .*(X(:,2)-mzh))/(n-1);

disp([‘Given means=’,num2str([mt,mz]));

disp([‘Estimated means=’,num2str([mth,mzh]));

disp([‘Covariance matrix=’,num2str([K(1,1),K(1,2),K(2,2)]));

disp([‘Estimated covariance matrix=’,num2str([st2,cv,sz2]));

4. С помощью команды run Lab1 выполните записанные операторы. Значения параметров, построенный график и выведенные на экран числа внесите в отчёт о выполнении лабораторной работы. Сделайте вывод о близости значений оценок математических ожиданий случайных величин t и z и оценок элементов ковариационной матрицы заданным значениям.

Контрольные вопросы.

1. В чём разница равномерного, экспоненциального и нормального распределений?

2. По каким формулам вычисляются математическое ожидание и дисперсия случайной величины?

3. Чему равны математическое ожидание и дисперсия экспоненциально распределённой случайной величины?

4. По каким формулам оцениваются математическое ожидание и дисперсия случайной величины?

5. Что такое ковариационная матрица и по каким формулам оцениваются её элементы?

6. Что будет построено в результате выполнения двух операторов X=mvnrnd([0,1],eye(2),1000); plot(X(:,1),X(:,2),’*’)?

7. Что такое гистограмма и как её построить в MATLAB?

8. Опишите действие операторов disp и num2str.