3.4.2. Подбор поперечной арматуры диафрагмы

Поперечная арматура в диафрагме ставится для обеспечения прочности по наклонным сечениям.

Расчет прочности изгибаемых элементов по бетонной полосе между наклонными сечениями имеет цель предотвращение разрушение элемента от действия сжимающих усилий вдоль полосы и производится из условия:

(3.4.11)

где,

- расчетное сопротивление бетона осевому растяжению (по первой группе предельных состояний);

- средняя ширина сечения диафрагмы.

Условие выполняется.

Конструктивно принимаем хомуты Ø6-A-400 с шагом 100мм.

Диафрагму армируем одним плоским сварным каркасом, который состоит из одного рабочего стержня продольной арматуры Ø16-А400, поперечных стержней – хомутов Ø6-А-400 с шагом на приопорном участке, равным l/4, S=100 мм; в пролёте S- 200 мм и конструктивного стержня, диаметр которого назначается из конструктивных соображений:

(3.4.12)

3.5.Расчет усилий и подбор арматуры в продольных ребрах

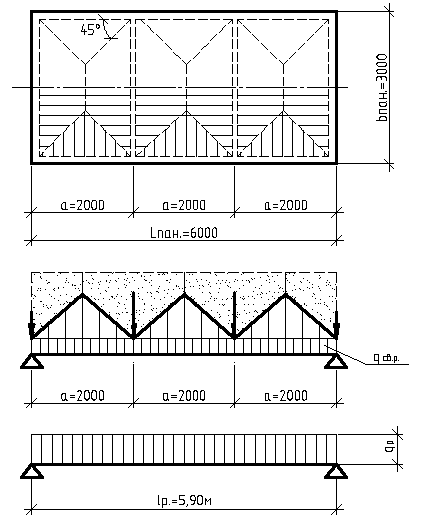
Рис.7. Схема загружения продольного ребра

Продольные ребра рассматриваются, как свободно опертые балки. Нагрузки на них передается непосредственно от плиты по закону треугольника. Практически нагрузку принимают равномерно распределенной:

(3.5.1)

где,

g и р – временная и постоянная расчетные нагрузки на 1м² (см. Таблицу сбор нагрузок);

- собственный вес 1п.м. ребра.

(3.5.2)

где - высота продольного ребра;

- средняя ширина ребра

; (3.5.3)

- объемный вес тяжелого бетона ;

- коэффициент надежности по нагрузке.

Наибольший изгибающий момент в середине пролета:

(3.5.4)

Наибольшая поперечная сила на опорах:

(3.5.5)

где,

- расчетный пролет ребра принимается равным, расстоянию между осями диафрагм:

(3.5.6)

При расчете арматуры в ребре необходимо учесть работу плит, часть которой попадает в сжатую зону. Поэтому профиль сечения ребра представляет собой полутавр с шириной полки:

(3.5.7)

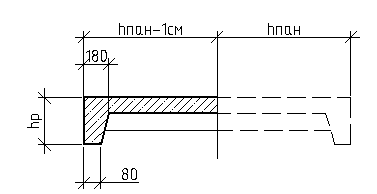
Рис.8.

Расчетный профиль будет зависеть от положения нейтральной оси, которое устанавливается проверкой условия:

(3.5.8)

где,

(3.5.9)

Условие выполняется, и площадь поперечной арматуры подбирается как для прямоугольного сечения шириной :

(3.5.10)

(3.5.11)

Принимаем верхний стержень Ø10-А-400, , нижний - Ø16-А-400, .