2 Полное исследование функции 1

2.1 Теоретическое введение

2.1.1 Экстремумы функции. Признаки возрастания и убывания функции

Рассмотрим график непрерывной функции. Из рис. 2.1 видно, что значение функции в точке x₁ меньше, чем значения функции в достаточно близких к ней точках, соседних с ней справа и слева. В этом случае говорят, что функция имеет в точке x₁ минимум.

  Рисунок 2.1

Точка x₀ называется точкой локального минимума функции f (x), если f (x) непрерывна в точке x₀ и существует такая окрестность точки x₀, что для всех x ≠ x₀ из этой окрестности выполняется неравенство f (x₀) < f(x). При этом говорят, что функция f (x) имеет минимум в точке x₀.  В точке x₂ (рис. 2.1) значение функции больше значений функции в достаточно близких к ней точках, расположенных справа и слева от нее. В этом случае говорят, что функция имеет в точке x₂ максимум.  Непрерывная в точке x₀ функция f (x) имеет максимум в точке x₀, если существует такая окрестность точки x₀, что для всех x ≠ x₀ из этой окрестности выполняется неравенство f (x₀) > f (x), при этом точка x₀ называется точкой максимума функции f (x).  Для точек максимума и минимума существует объединяющий их термин – точки экстремума, а значения функции в этих точках называются экстремумами функции.  Из приведенных определений следует, что экстремум функции имеет локальный характер – это наибольшее или наименьшее значение функции по сравнению с близлежащими значениями. На промежутке функция может иметь несколько экстремумов, причем может оказаться, что какой-либо минимум функции больше какого-либо максимума. Следующая теорема позволяет ответить на вопрос, в каких точках функция может достигать экстремума.  Теорема Ферма (необходимый признак экстремума). Если функция  f (x) дифференцируема в точке x₀ и имеет в этой точке экстремум, то ее производная при x = x₀ обращается в нуль, т.е.  f ' (x₀) = 0.  Теорема Ферма имеет простое геометрическое истолкование. Так как производная в точке x₀ равна угловому коэффициенту касательной к графику функции в этой точке, то равенство  f ' (x₀) = tg α = 0 означает, что α = 0 , т.е. касательная к кривой в точке экстремума дифференцируемой функции параллельна оси Ox (рис. 2.1).  Таким образом, дифференцируемая функция может иметь экстремум лишь в тех точках, где производная равна нулю. Однако функция может иметь экстремум и в тех точках области определения, где производная не существует. Например, функция y = |x| в точке x = 0 достигает минимума, но не дифференцируема при x = 0 (см. раздел 1, рис. 1.17). Функция, изображенная на рис. 1.2, имеет в точке x₀ максимум, но не дифференцируема в этой точке. так как при x = x₀ касательная к кривой образует с осью Ох угол 90° (f ' (x₀) = tg 90º = ∞).

  Рисунок 2.2

Условия   f ' (x₀) = 0 и   f ' (x₀) не существует являются необходимыми условиями экстремума, но не достаточными, поскольку можно привести примеры функций, для которых эти условия выполняются, но экстремума в соответствующей точке функция не имеет. Например, функция   f (x) = x³ имеет производную   f ' (x) = 3x², которая обращается в нуль при x = 0, однако в точке x = 0 функция экстремума не имеет (см. раздел 1, рис. 1.1).  Те значения аргумента, при которых функция  f (x) сохраняет непрерывность, а ее производная  f ' (x) обращается в нуль или не существует, называются критическими точками (или критическими значениями аргумента).  Если во всех точках некоторого промежутка  f ' (x) = 0, то функция  f (x) сохраняет в этом промежутке постоянное значение. Если во всех точках некоторого промежутка  f ' (x) > 0, то функция  f (x) возрастает в этом промежутке (достаточный признак возрастания). Если во всех точках некоторого промежутка  f ' (x) < 0, то  f (x) убывает на этом промежутке (достаточный признак убывания).  Из вышеизложенного следует, что экстремум функции может достигаться только в критических точках, т. е. в тех точках, в которых  f (x) непрерывна,  f ' (x) = 0, либо  f ' (x) = ∞, либо  f ' (x) не существует. Но это является лишь необходимым признаком экстремума, так как не в каждой критической точке экстремум существует. Поэтому нужно располагать достаточными признаками, позволяющими судить, имеется ли в конкретной критической точке экстремум и какой именно, максимум или минимум.

Теорема (первый достаточный признак экстремума). Если x₀ – критическая точка функции f (x) и в некоторой окрестности этой точки, слева и справа от нее, производная имеет противоположные знаки, то f (x₀) является экстремумом функции, причем:  1) максимумом, если f ' (x) > 0 при x < x₀ и f ' (x) < 0 при x > x₀;  2) минимумом, если f ' (x) < 0 при x < x₀ и f ' (x) > 0 при x > x₀.  Таким образом, если x₀ – критическая точка f (x) и при переходе через x₀ производная f ' (x) меняет знак, то x₀ есть точка экстремума, причем точка максимума, если производная меняет знак с плюса на минус, и точка минимума, если – с минуса на плюс. В противном случае в точке x₀ экстремума нет.  Теперь нетрудно сделать практические выводы. Пусть речь идет об отыскании экстремумов функции, непрерывной в некотором промежутке и имеющей в нем конечное множество критических точек. Отыскав все критические точки, нужно расположить их в порядке возрастания: a < x₁ < x₂ < ... < x_n < b, где a и b – концы промежутка. Так как все точки, в которыхf ' (x) = 0 или f ' (x) не существует, входят в число точек x₁, x₂, ..., x_n, то в каждом из интервалов (a, x₁), (x₁, x₂), ..., (x_n, b) существует производная f ' (x) ≠ 0, которая внутри интервала сохраняет знак (функция внутри интервала монотонна). Поэтому, чтобы установить знак производной в указанных интервалах, достаточно взять в каждом интервале по одной контрольной точке и установить знак производной в этой точке.  Последовательности интервалов монотонности функции соответствует некоторая последовательность плюсов и минусов, характер чередования которых на основании первого достаточного признака экстремума позволит судить о наличии максимума, минимума или об отсутствии экстремума в соответствующей точке.  Пример. Исследуем на экстремум функцию y =   и построим ее график.  Решение. Функция определена и непрерывна на всей числовой прямой, т.е. x є R. Ее производная f ' (x) = x²(x – 3) существует также на всей числовой прямой. Поэтому в данном случае критическими точками служат лишь те, в которых   f ' (x) = 0, т. е. x² (x – 3) = 0, откуда x₁ = 0 и x₂ = 3. Критические точки x₁ = 0 и x₂ = 3 разбивают всю область определения функции на три интервала монотонности: (–∞, 0), (0, 3), (3, +∞). Выберем в каждом из них по одной контрольной точке и найдем знак производной в этой точке.  Для интервала (–∞, 0) контрольной точкой может служить x = – 1; находим  f ' (– 1) < 0. Взяв в интервале (0, 3) точку x = 1, получим   f ' (1) < 0, а взяв в интервале (0, 3) точку x = 4, имеем   f ' (4) > 0. Итак, в интервалах (–∞, 0) и (0, 3)  f ' (x) < 0, а в интервале (3, +∞)   f ' (x) > 0. Согласно первому достаточному признаку экстремума, в точке x = 0 экстремума нет (так как производная сохраняет знак в интервале (–∞, 3)), а в точке x = 3 функция имеет минимум (поскольку производная при переходе через эту точку меняет знак с минуса на плюс). Найдем соответствующие значения функции: f (0) = 0,  f (3) = – 6,75. В интервале (–∞, 3) функция убывает, так как в этом интервале  f ' (x) < 0, а в интервале (3, +∞) – возрастает, так как в этом интервале   f ' (x) > 0.  Чтобы уточнить построение графика, найдем точки пересечения его с осями координат. При y = 0 получим уравнение   = 0, корни которого x₁ = 0 и x₂ = 4, т.е. найдены две точки (0; 0) и (4; 0) графика функции. Используя все полученные сведения, строим график (рис. 2.3). Заметим, что из условия  f ' (0) = 0 следует, что касательная к графику функции при x = 0 горизонтальна, т.е. в точке (0; 0) ось Ox является касательной к графику функции. 

  Рисунок 2.3

Исследование на экстремум может выполняться и с помощью второй производной.

Теорема. (Второй достаточный признак экстремума). Если функция   f (x) дважды дифференцируема в окрестности точки x₀,   f '' (x) непрерывна в точке x₀ и в точке x₀выполняются условия:   f ' (x₀) = 0,   f '' (x₀) ≠ 0, то в этой точке функция имеет экстремум, причем максимум, если   f '' (x₀) < 0, и минимум, если   f '' (x₀) > 0.  Пример. Исследовать на экстремум функцию 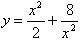  и построить ее график.  Решение. Областью определения функции является числовая прямая кроме точки x = 0, т.е. D = (–∞, 0) (0, +∞).  Для сокращения исследования можно воспользоваться тем, что данная функция четная, так как 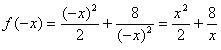 . Поэтому ее график симметричен относительно осиOy и исследование можно выполнить только для интервала (0, +∞).  Haходим производную  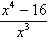 и критические точки функции:  1) y ' = 0   =>     = 0   =>   x⁴ – 16 = 0   =>   x = –2   и   x = 2;  2) y ' = ∞   =>     = ∞   =>   x = 0,  но функция терпит разрыв в этой точке, поэтому она не может быть точкой экстремума.  Таким образом, заданная функция имеет две критические точки: x₁ = –2   и   x₂ = 2. Учитывая четность функции, проверим по второму достаточному признаку экстремума только точку x = 2. Для этого найдем вторую производную y'' (x) =   и определим ее знак при x = 2; получим f '' (2) > 0. Так как f (2) = 0 и f '' (2) > 0, то x = 2 является точкой минимума функции; при этом y_min = f (2) = 4.  Чтобы составить более полное представление о графике функции, выясним ее поведение на границах области определения: 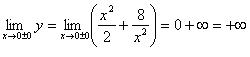   (здесь символом x → 0 + 0 обозначено стремление x к нулю справа, причем x остается положительным; аналогично, x → 0 – 0 означает стремление x к нулю слева, причем xостается отрицательным). Таким образом, если x → 0 ± 0, то y → + ∞. Далее, находим 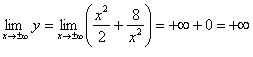 ,  т.е. если x → ± ∞, то y → +∞.  Точек пересечения с осями график функции не имеет. Он изображен на рис. 2.4. 

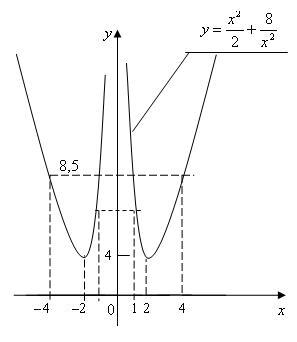  Рисунок 2.4

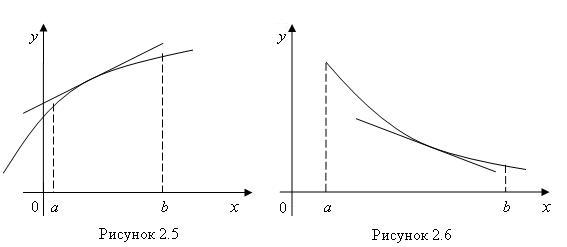
2.1.2 Направление выпуклости графика функции. Точки перегиба  Пусть функция f (x) дифференцируема на интервале (a; b), тогда в любой точке x є (a, b) существует касательная к графику этой функции. График дифференцируемой функции называется выпуклым вверх в интервале (a, b), если в этом интервале он расположен ниже любой своей касательной (рис. 2.5). График дифференцируемой функции называется,выпуклым вниз в интервале (a, b), если в этом интервале он расположен выше любой своей касательной (рис. 2.6). 

Теорема. Достаточный признак направления выпуклости графика функции. Если для функции f (x) во всех точках интервала (a; b)   f '' (x) > 0, то кривая y = f (x) выпукла вниз в этом интервале; если же   f '' (x) < 0 во всех точках интервала (a; b), то кривая выпукла вверх в этом интервале.  Точка (x₀, f (x₀)) графика непрерывной функции, в которой изменяется направление выпуклости, называется точкой перегиба графика функции, а x₀ называется точкой перегиба функции.  Из определения следует, что с одной стороны от точки перегиба кривая расположена под касательной, с другой стороны – над ней, или наоборот. Поэтому точку перегиба на графике принято показывать отрезком касательной, которая в этой точке пересекает кривую (рис. 2.7). 

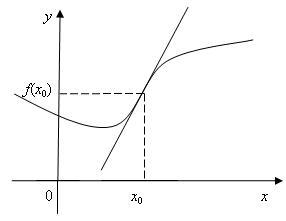  Рисунок 2.7

Теорема. Достаточный признак существования точки перегиба. Если в точке x₀ функция f (x) имеет первую производную f ' (x₀), а вторая производная f '' (x₀) в этой точке равна нулю или не существует и, кроме того, f'' (x) при переходе через x₀ меняет знак, то (x₀; f (x₀)) является точкой перегиба графика функции y = f (x).  Таким образом, чтобы исследовать характер выпуклости кривой y = f (x), нужно найти те точки, в которых f'' (x) = 0 или  f '' (x) не существует, а затем, используя достаточный признак, исследовать знаки второй производной слева и справа от каждой возможной точки перегиба (подобно тому, как определялись точки экстремума по первой производной).

Пример. Найдем точки перегиба и построим график функции  .  Решение. Функция определена при x є (– ∞; + ∞). Ее производные   и  . Здесь f '' (x) = ∞ при x = 0, причем  f '' (x) > 0 при х < 0 и f '' (x) < 0 при х > 0. Следовательно, слева от x = 0 кривая выпукла вниз, а справа – выпукла вверх, т.е. О(0; 0) – точка перегиба графика. В этой точке угловой коэффициент касательной k_x=1/2 = f ' (0) = ∞, поэтому касательная вертикальна (рис. 2.8). 

  Рисунок 2.8

2.1.3 Асимптоты  Выше было показано, как нахождение точек экстремума и точек перегиба упрощает построение графика и дает возможность установить характерные особенности изменения функции. Во многих случаях построение графика функции облегчается, если предварительно построить асимптоты кривой. Различают три вида асимптот: вертикальные, горизонтальные и наклонные.  Прямая x = a является вертикальной асимптотой графика функции  f (х), если выполняется хотя бы одно из условий:   или   (при этом функция  f (х) может быть вообще не определена соответственно при x ≥ a или x ≤ a).  Из сказанного следует, что вертикальные асимптоты кривой нужно искать в точках разрыва и на границах области определения. График функции, непрерывной на всей числовой прямой, вертикальных асимптот не имеет. Например, график функции y = ln х имеет вертикальную асимптоту х = 0 на границе области определения, так как   (см. раздел 1, рис. 1.6).  Если  , то y = b – горизонтальная асимптота кривой у = f (x) (правая при x → + ∞, левая при x → – ∞ и двусторонняя, если пределы при x → ± ∞ равны).  Например, график функции y = a^x при а > 1 имеет левую горизонтальную асимптоту у = 0, так как  . Правой горизонтальной асимптоты у кривой нет, поскольку   (см. раздел 1, рис. 1.5).  Прямая y = kx + b называется наклонной асимптотой графика функции у = f (x), если   (левая наклонная асимптота) или   (правая наклонная асимптота).  Существование наклонной асимптоты определяется следующим условием. Для того чтобы кривая у = f (x) имела асимптоту у = kx + b, необходимо и достаточно, чтобы существовали конечные пределы

(2.1)

или

(2.2)

В первом случае получается правая наклонная асимптота, во втором – левая. Правая наклонная асимптота изображена на рис. 2.9. 

  Рисунок 2.9

При совпадении пределов (2.1) и (2.2) прямая у = kx + b является двусторонней асимптотой кривой. Если хотя бы один из пределов, определяющих асимптоту у = kx + b, не существует, то график функции не имеет наклонной асимптоты (но может иметь вертикальную).  Нетрудно видеть, что горизонтальная асимптота у = b является частным случаем наклонной у = kx + b при k = 0. Поэтому если в каком–либо направлении кривая имеет горизонтальную асимптоту, то в этом направлении нет наклонной, и наоборот.  Пример. Найдем асимптоты графика функции   и построим эскиз графика.  Решение. Функции определена на всей числовой прямой, кроме x = 0, т.е. D(f) = (–∞, 0)  (0, +∞), Поэтому в точке разрыва x = 0 кривая может иметь вертикальную асимптоту. Действительно,    Аналогично,    Следовательно, x = 0 – вертикальная асимптота; при x → 0 слева   f (x) → +∞, при x → 0 справа   f (x) → –∞.  Горизонтальной асимптоты кривая не имеет, так как    Выясним наличие наклонной асимптоты:      Прямая у = 2x является двусторонней наклонной асимптотой заданной кривой (рис. 2.10). 

  Рисунок 2.10

2.1.4 Общая схема исследование функций и построение графиков  Как следует из вышеизложенного, с помощью дифференциального исчисления и теории пределов можно установить характерные особенности изменения функций: возрастание и убывание, максимумы и минимумы, направление выпуклости графика, наличие асимптот. Характерные точки – точки разрыва, экстремума, перегиба, пересечения графика с осями координат – служат опорными точками при исследовании функций и построение их графиков.  Обычно используют следующую схему исследования функции.  1. Находят область определения, интервалы непрерывности и точки разрыва функции.  2. Исследуют функцию на четность или нечетность (осевая или центральная симметрия графика), на периодичность. Если функция четная или нечетная, достаточно построить ее на промежутке [0; +∞), а затем использовать соответствующую симметрию. Если функция периодическая, достаточно построить ее на любом отрезке, равном длине периода, а затем периодически продолжить.  3. Находят точки пересечения кривой с осями координат, если они существуют.  4. Находят интервалы постоянства знака функции, т.е. интервалы, где функция положительна и где функция отрицательна.  5. Находят асимптоты (вертикальные, горизонтальные или наклонные). Исследуют характер точек разрыва.  6. Строят эскиз графика функции.  7. Находят интервалы монотонности функции, точки ее экстремума.  8. Находят интервалы выпуклости вверх и выпуклости вниз кривой, точки ее перегиба.  9. Строят график функции.