4.2 Теплообмен при конденсации пара

Конденсация –– это переход вещества из газообразного состояния в жидкое либо в твердое³. Она может происходить в объёме пара или паро-газовой смеси либо на поверхности твердого тела или жидкости, с которой пар (смесь) находится в контакте. Для конденсации необходимо, чтобы температура этой поверхности была ниже температуры насыщения пара.

Различают два вида конденсации: плёночную и капельную. При плёночной на поверхности твердого тела, хорошо смачиваемой жидкостью, образуется сплошная плёнка конденсата, при капельной на несмачиваемой жидкостью поверхности образуются отдельные капли конденсата. Иногда возможна смешанная конденсация, когда на различных участках поверхности наблюдаются как плёночная, так и капельная конденсация. Конденсацию пара непосредственно на поверхности жидкости называют контактной.

В стационарном процессе плёночной конденсации теплота, выделяющаяся на внешней границе плёнки, отводится к поверхности охлаждения, от которой её необходимо непрерывно отводить. При ламинарном движении плёнки перенос теплоты осуществляется только теплопроводностью в поперечном направлении. Если температура внешней поверхности плёнки равна температуре насыщения t_s, то плотность теплового потока равна

,

(4.18)

где λ – коэффициент теплопроводности конденсата,

δ – толщина плёнки,

t_с – температура поверхности охлаждения.

В то же время по уравнению Ньтона – Рихмана

,

(4.19)

Приравняв правые части выражений (4.18) и (4.19), получим

.

(4.20)

Следовательно, определение коэффициента теплоотдачи при плёночной конденсации сводится к определению толщины плёнки δ из анализа условий её течения. Такой анализ впервые выполнил Нуссельт, введя отмеченные выше допущения о ламинарном движении плёнки и отсутствии в ней конвекции, скачка температуры и трения на границе пар–плёнка. Он использовал также допущения о том, что значения температуры стенки и внешней поверхности плёнки постоянны, теплофизические свойства конденсата не зависят от температуры, силы инерции пренебрежимо малы по сравнению с силами тяжести и трения, силы поверхностного натяжения на внешней поверхности плёнки не влияют на характер её движения. При этих допущениях дифференциальное уравнение движения единичного объёма конденсата в плёнке, образующейся на вертикальной стенке (рис.4.3), имеет вид

.

(4.21)

Проинтегрировав уравнение (4.21) с учетом пограничных условий (при y=0 w_x=0 и при y=δ w_x/y =0), получим закон распределения скоростей w_x в слое конденсата. Зная этот закон, можно определить количество жидкости M, протекающей в единицу времени через сечение х при ширине стенки, равной единице

.

(4.22)

Из (4.22) следует, что толщина плёнки увеличивается с ростом расхода жидкости по закону δ .

Рис.4.3. Пленочная конденсация на вертикально стенке.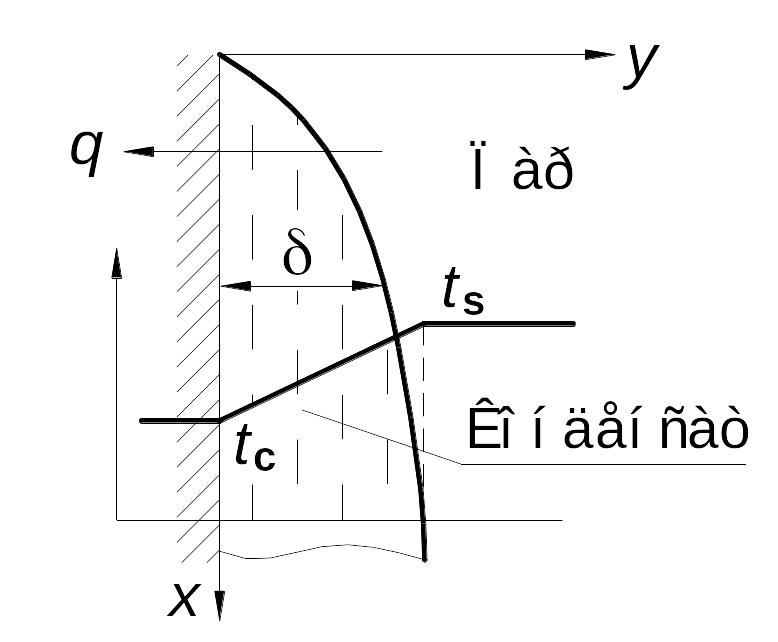

Величина М входит также в уравнение теплового баланса для участка плёнки длиной х при ширине стенки, равной единице

.

(4.23)

Из уравнения (4.23) можно определить толщину плёнки δ

.

(4.24)

Располагая выражением для δ, из формулы (4.20) можно определить локальный коэффициент теплоотдачи

.

(4.25)

Среднее значение для вертикальной стенки либо трубы высотой h определяется по формуле

,

(4.26)

где величина зависит только от свойств жидкости

Из (4.26) следует, что значение уменьшается с ростом высоты h и разности температур t = t_s – t_c.

Полагая, что значение  пренебрежимо мало по сравнению с , то есть массовые силы приложены только к более тяжелой фазе, можно представит выражение (4.26) в безразмерном виде

,

(4.27)

где – число Галилея, характеризующее отношение сил тяже-

сти к силам внутреннего трения;

– число Кутателадзе.

Если стенка наклонена под углом  к горизонту, в уравнении движения вместо ускорения силы тяжести g входит его составляющая в направлении течения плёнки, равная gsin. Поэтому формула для расчета коэффициента теплоотдачи принимает вид

.

(4.28)

Для горизонтальной трубы диаметром d Нуссельт также выполнил вывод, аналогичный приведенному выше, и получил следующую формулу для среднего коэффициента теплоотдачи:

.

(4.29)

Формула (4.29) получена при условии t_c=const. При q = const коэффициент 0,728 следует заменить на 0,693.

При конденсации на горизонтальном пучке труб с n рядами по вертикали средний коэффициент теплоотдачи пучка определяют по формуле

,

(4.30)

где – коэффициент теплоотдачи первого ряда.

В связи с принятыми при выводах допущениями полученные формулы для коэффициента теплоотдачи являются приблизительными, но закономерности плёночной конденсации теория Нуссельта отражает верно. Учёт сил инерции, конвективного переноса теплоты в плёнке и переохлаждения конденсата показывает, что при значениях K>5 и 1<Pr<100 различие в значениях  по сравнению с решением Нуссельта не превышает нескольких процентов. Поэтому коэффициент теплоотдачи при плёночной конденсации целесообразно рассчитывать по формулам (4.26)– (4.30), относя все теплофизические свойства жидкости к температуре насыщения и вводя поправочный множитель _t, учитывающий зависимость этих свойств от температуры

.

(4.31)

В формуле (4.31) индексы с и s означают, что значения свойств выбираются соответственно при температуре стенки t_c и температуре насыщения t_s.

На поверхности вертикальных труб и пластин наблюдается волновое течение плёнки конденсата, что увеличивает интенсивность теплоотдачи, так как при волновом движении средняя по времени толщина плёнки меньше рассчитанной по формуле Нуссельта. Поправочный множитель к величине , учитывающий это явление, имеет вид

,

(4.32)

где – число Рейнольдса для плёнки конденсата⁴.

Число Re_s можно выразить через теплообменные характеристики процесса

.

(4.33)

При значениях Re4 ε_=1, так как волнового течения плёнки нет. С увеличением расхода жидкости в плёнке, а значит числа Re_s, волнообразование нарастает и значение ε_ увеличивается. Например, при Re=100 ε_=1,14, при Re=400 ε_=1,2, при Re_кр=1600 ε_ =1,27.

С учетом обеих поправок значение при конденсации пара на поверхности вертикальных труб и пластин равно

.

(4.34)

Поскольку величина входит в выражение для Re_s, её расчет первоначально проводят при значении ε_ =1, затем определяют число Re_s по формуле (4.33), а после этого рассчитывают поправку ε_ и уточняют значение .

Для развитого волнового течения необходим участок протяженностью в несколько длин волн. Поэтому для горизонтальных труб поправку ε_ следует вводить только тогда, когда диаметр трубы удовлетворяет соотношению

.

(4.35)

При большой высоте поверхности и значительных температурных напорах расход конденсата возрастает, и в нижней части поверхности возникает участок с турбулентным режимом течения плёнки. Этому режиму соответствуют значения числа Re_s, превышающие критическое Re_кр = 1600 (либо значения комплекса свыше 2300). Среднее значение коэффициента теплоотдачи для вертикальной поверхности, на которой имеются ламинарный и турбулентный участки течения конденсата, рассчитывают по уравнению

.

(4.36)

Теплофизические свойства в (4.36) выбирают по температуре насыщения.

Если Re_s> Re_sкр, то есть зона турбулентного течения плёнки занимает бóльшую часть поверхности конденсации, то при заданной плотности теплового потока среднее значение рассчитывают по уравнению

.

(4.37)

где l_g– характерный размер, равный

.

(4.38)

Приведенные выше соотношения справедливы при конденсации чистого насыщенного пара на чистой поверхности. При определении коэффициента теплопередачи для реальных условий целесообразно учитывать дополнительные факторы, влияющие на теплоотдачу. В частности, при конденсации перегретого пара следует вместо теплоты фазового перехода r подставлять в формулы значение r=r+q_п, где q_п – теплота перегрева, равная разности энтальпий перегретого и насыщенного пара. При этом в качестве разности температур по-прежнему принимают величину t=t_s – t_c, так как перегретый пар вблизи стенки охлаждается и становится насыщенным. При конденсации влажного пара r= rх, где х – степень сухости.

Если поверхность шероховата либо покрыта окислами, толщина плёнки увеличивается и значение  снижается. К тому же плёнка окислов оказывает дополнительное термическое сопротивление передаче теплоты стенке.

При наличии в паре воздуха либо других неконденсирующихся газов теплоотдача при конденсации резко уменьшается, так как у стенки образуется зона с повышенным содержанием газа. Через эту зону молекулы пара проникают к стенке лишь путем диффузии. При содержании в паре 0,4% воздуха коэффициент теплоотдачи снижается на 40 %, а при содержании 1% воздуха – на 60 %. Поэтому из конденсаторов паротурбинных установок воздух непрерывно удаляют с помощью эжекторов.

Поток пара при больших скоростях воздействует на плёнку конденсата. Если движение пара совпадает с направлением течения плёнки, её толщина уменьшается и значение возрастает. При встречном движении пара толщина плёнки увеличивается и значение уменьшается, но при весьма высокой скорости пар может сорвать часть плёнки, и тогда возрастает.

На теплопередачу при конденсации влияет также компоновка поверхности теплообменного аппарата. В многорядных пучках конденсат с верхних рядов стекает на нижние. Поэтому следует размещать трубы не строго друг под другом, а со смещением по горизонтали, чтобы стекающие капли либо струйки конденсата «срывали» плёнку с нижних труб. Для вертикальных туб коэффициент теплоотдачи в нижней части уменьшается в связи с утолщением плёнки. Среднее значение можно увеличить установкой по высоте трубы колпачков, отводящих конденсат от трубы. Например, при высоте трубы 3 м и расстоянии между колпачками 0,1 м значение возрастает в 2–3 раза.

Необходимы также профилактические меры против отложения на поверхности конденсации масла и других загрязнений. Поэтому в холодильной установке устанавливают маслоотделитель после компрессора.

При конденсации пара в трубах на плёнку конденсата воздействует паровой поток и сила тяжести. Характер движения конденсата зависит от ориентации трубы в пространстве и скорости пара. В вертикальных трубах при движении пара сверху вниз силы тяжести и динамического воздействия парового потока направлены одинаково и плёнка конденсата стекает вниз. При увеличении скорости пара толщина плёнки уменьшается и интенсивность теплоотдачи возрастает. В горизонтальных трубах конденсат стекает по внутренней поверхности вниз, поэтому интенсивность теплоотдачи в верхней части трубы выше, чем в нижней.

Различают режимы полной и частичной конденсации пара. В первом случае из трубы вытекает сплошной поток конденсата, во втором – парожидкостная смесь. Для любого поперечного сечения трубы уравнение материального баланса имеет вид

,

(4.39)

где индексами  и  обозначены расходы пара и жидкости.

Отношение расхода пара М, проходящего через данное сечение, к полному расходу М называют расходным массовым паросодержанием двухфазного потока и обозначают буквой х (как и степень сухости влажного пара).

Уравнение теплового баланса для трубы диаметром d имеет вид

,

(4.40)

где – средняя по длине трубы l плотность теплового потока,

х₁ и х₂ – массовые паросодержания на входе в трубу и на выходе из неё.

Из (4.40) видно, что чем больше тепловая нагрузка и чем длиннее труба, тем выше должны быть расход и скорость потока. В этих условиях течение плёнки конденсата в основном определяется динамическим воздействием парового потока и на бòльшей части длины имеет турбулентный характер.

Средний коэффициент теплоотдачи по всей длине трубы при турбулентном течении конденсата внутри трубы определяют по формуле

,

(4.41)

где ₀ – коэффициент теплоотдачи, рассчитанный по формуле (3.14) при турбулентном движении жидкости в трубе с расходом М;

_m – средняя плотность парожидкостной смеси в данном сечении трубы.

Индексами 1 и 2 обозначены свойства во входном и выходном сечениях.

Отношение плотностей жидкости и пароводяной смеси , входящее в уравнений (4.41), рассчитывают по формуле

.

(4.42)

Если жидкость не смачивает поверхность охлаждения, наблюдается капельная конденсация пара. Скорость роста капель вначале велика, но с увеличением их размеров уменьшается. Отдельные капли непрерывно объединяются и скатываются с поверхности под влиянием силы тяжести, когда их размеры достигают нескольких миллиметров. Количество капель на поверхности увеличивается с ростом температурного напора t=t_s–t_c.

Зависимость коэффициента теплоотдачи  от температурного напора t при капельной конденсации неподвижного насыщенного водяного пара представлена на рис. 4.4, полученном на основании экспериментальных данных; из графика видно, что значения  весьма велики. Теплоотдача интенсифицируется при движении пара, но при значительных температурных напорах среднее значение  при капельной конденсации движущегося пара мало отличается от такового для неподвижного пара.

Рис.4.4. Теплоотдача при капельной конденсации водяного пара в зависимости от t_s и t.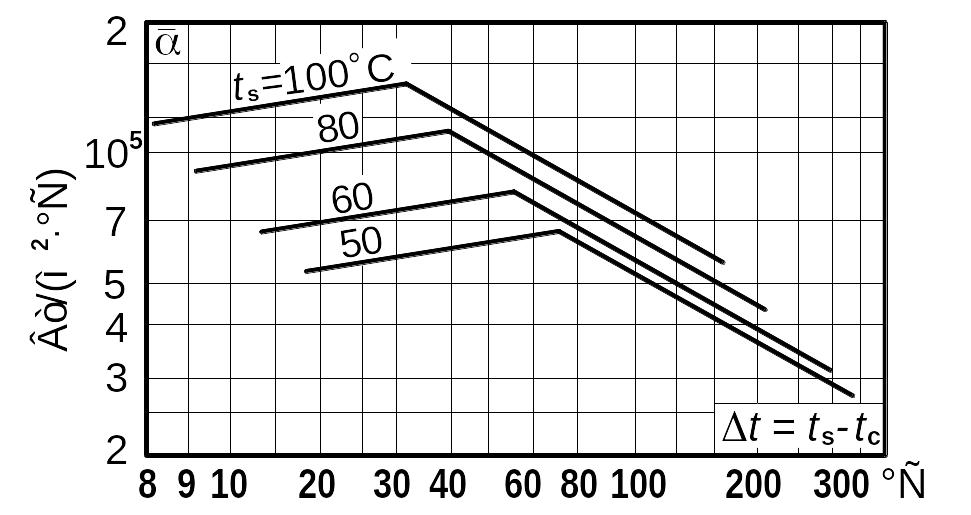

При конденсации пара на поверхности пучка горизонтальных труб попадание капель с верхних труб на нижние уменьшает значение  на 10–15%. Более существенное снижение коэффициента теплоотдачи происходит при наличии в паре даже небольших примесей неконденсирующихся газов.

1Определяется как полное сечение канала минус произведение диаметра трубы на длину

2 В отличие от испарения, которое представляет собой парообразование с поверхности жидкости при любой температуре.

3 Переход из газообразного состояния в твердое называется десублимацией

4 Это соотношение следует из общего определения числа Рейнольдса: ; для плёнки d_экв=4δ, поэтому согласно уравнению (4.23) величина .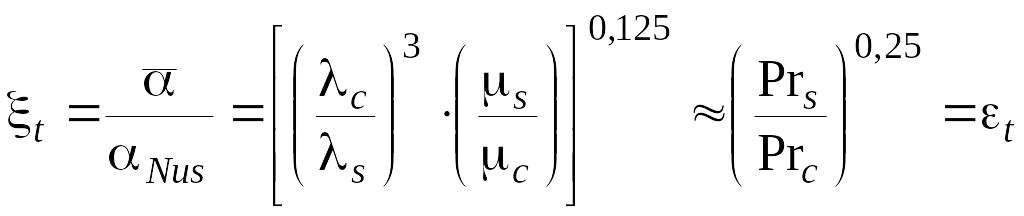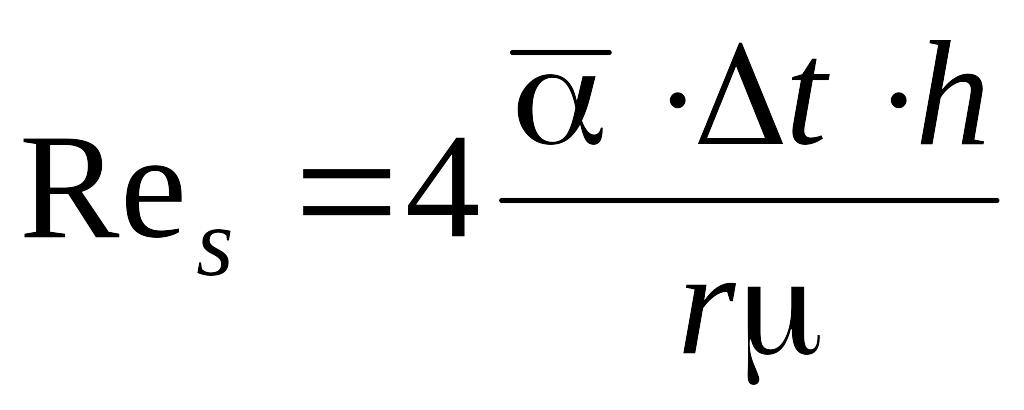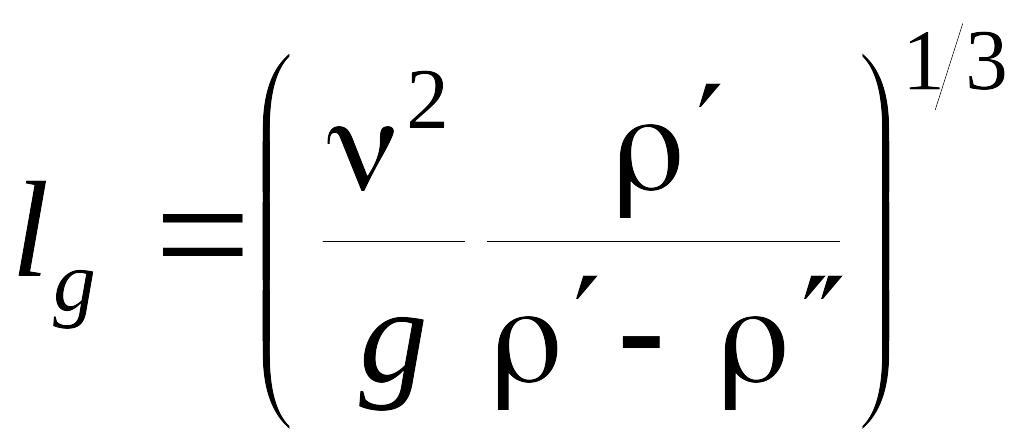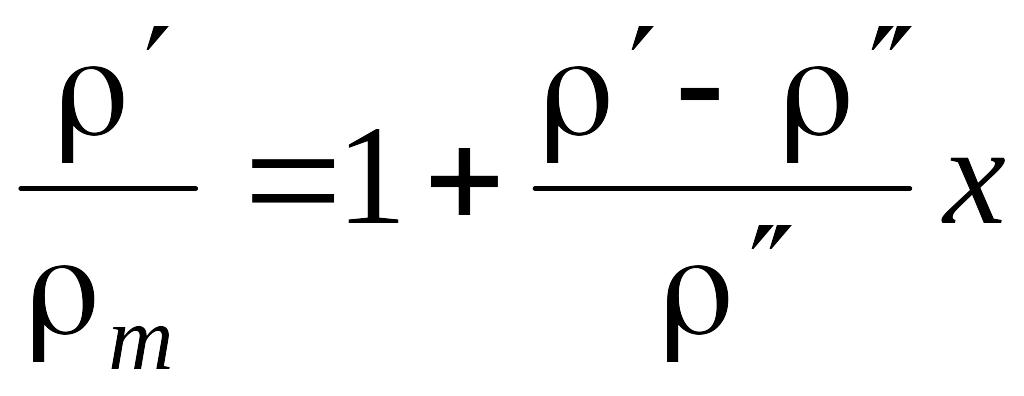