Раздел 1. Предел и непрерывность функции.

1.1 Предел функции

Пусть функция определена на некотором промежутке и пусть точка или . Составим из множества последовательность точек: , сходящихся к точке . Значения функции в этих точках также образуют последовательность:

• Число А называется пределом функции при , стремящемся к , если для любого числа найдется такое число , что при всех , удовлетворяющих неравенству , будет выполняться неравенство:

Определение предела можно сформулировать еще и так:

• Число А называется пределом функции при стремящемся к , если при любом существует такая окрестность точки , что для любого из этой окрестности . Это записывают так:.

1.2.Односторонние (левый и правый) пределы.

Левый предел – это односторонний предел функции, когда последовательность значений аргумента слева от точки , т.е. .

Символическая запись левого предела функции:

Правый предел – это односторонний предел функции, когда последовательность значений аргумента справа от точки , т.е. .

Символическая запись левого предела функции:

Теорема (о существовании предела функции в точке). Функция имеет в точке предел тогда и только тогда, когда в этой точке существуют левый и правый пределы, и они равны. В таком случае предел функции равен односторонним пределам.

1.3.Основные теоремы о пределах.

1. Если С – постоянная величина, то .

2. Если С – постоянная величина, то

Арифметические операции над функциями, имеющими предел в точке , приводят к функциям также имеющим предел в этой точке.

Пусть функции и имеют в точке пределы Аи В :

3. Предел алгебраической суммы равен алгебраической сумме пределов:

4. Предел произведения равен произведению пределов: .

5. Предел отношения равен отношению пределов, если предел знаменателя отличен от нуля:

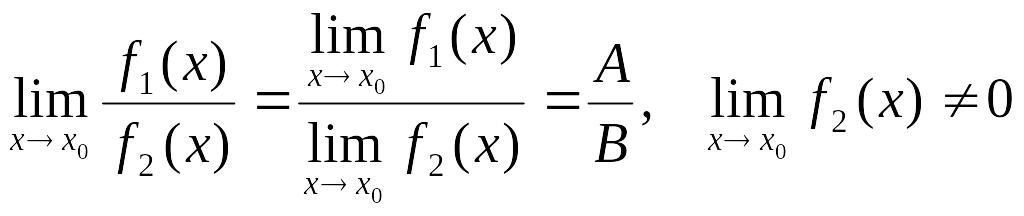
6. Предел целой положительной степени переменой величины равен той же степени предела этой же переменной.

1.4.Предел функции на бесконечности.

• Число называется пределом функции на бесконечности (или при , стремящемся к бесконечности). Если для всех достаточно больших по модулю значений аргумента соответствующие значения функции сколь угодно мало отличаются от числа .

Из рисунка видно, что ординаты, изображающие значения функции, сколь угодно мало отличаются от числа для любых достаточно больших значений .

Рисунок 1.

1.5.Способы вычисления пределов функций.

1.5.1. Непосредственное вычисление предела функции в точке.

Для вычисления предела функции при надо вместо переменной подставить значение , к которому она стремится, и посчитать, используя соответствующие теоретические положения.

Пример 1. Вычислите предел функции

Пример 2. Вычислите предел функции