3. Интегрирование по частям.

Если и -функции от , имеющие непрерывные производные, то вычисление определенного интеграла интегрированием по частям проводится по формуле:

Пример 44. Найти определенный интеграл .

Решение.

Пример 45. Найти определенный интеграл .

Решение.

3.2.3. Применение определенного интеграла для решения прикладных задач.

1. Вычисление площадей плоских фигур.

Как известно определенный интеграл от непрерывной неотрицательной функции равен площади соответствующей криволинейной трапеции (геометрический смысл определенного интеграла): .

С помощью определенного интеграла можно также вычислять площади плоских фигур, т.к. эта задача сводится к вычислению площадей криволинейных трапеций.

Площадь всякой плоской фигуры в прямоугольной системе координат может быть составлена из площадей криволинейных трапеций прилегающих к оси или к оси .

При вычислении площадей плоских фигур возможны следующие случаи:

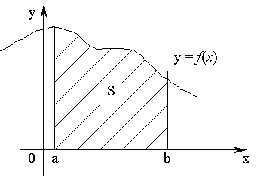
1. П усть функция непрерывна и неотрицательна на отрезке . Тогда площадь соответствующей криволинейной трапеции находится по формуле

Рисунок 15

2. В том случае, когда непрерывная функция на отрезке , для вычисления площади соответствующей фигуры следует использовать ф ормулу : Рисунок 16

3. Пусть функция непрерывна на отрезке и принимает на этом отрезке как положительные так и отрицательные значения. Тогда нужно разбить отрезок на такие части, в каждой из которых функция не изменяет свой знак, затем вычислить по приведенным выше формулам соответствующие этим частям площади и эти площади с ложить. Например, площадь фигуры, изображенной на рис.17 равна:

Рисунок 17

4. Площадь фигуры, ограниченной графиками двух непрерывных

ф ункций и на отрезке находится по формуле : Рисунок 18

5. П лощадь фигуры, ограниченной графиками непрерывных функций и и осью находится по формуле : Рисунок 19

Задачи на вычисление площадей плоских фигур удобно решать по следующему плану:

1. По условию задачи выполнить рисунок плоской фигуры, площадь которой нужно найти. Для этого построить графики функций в одной системе координат.

2. Найти абсциссы точке пересечения графиков функций ( пределы интегрирования), т.е. решить уравнение .

3. Записать формулу для вычисления площади фигуры и вычислить интеграл.

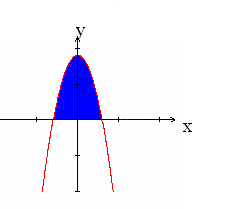
Пример 46. Вычислить площадь фигуры, ограниченной графиком функции и осью .

Решение.

₁

. Выполним рисунок фигуры площадь которой нужно найти.

_{2. Найдем пределы интегрирования. Для этого решим уравнение : . 3. Вычислим площадь фигуры по формуле: Ответ.}

_{Пример 47. Вычислить площадь фигуры, ограниченной графиками функций} и .

Решение.

1. П остроим графики функций в одной системе координат.

2. Найдем пределы интегрирования. Для этого решим уравнение

3. В ычислим площадь фигуры по формуле

Ответ.

_{Пример 48. Вычислить площадь фигуры, ограниченной графиками функций , и осью .}

_{Р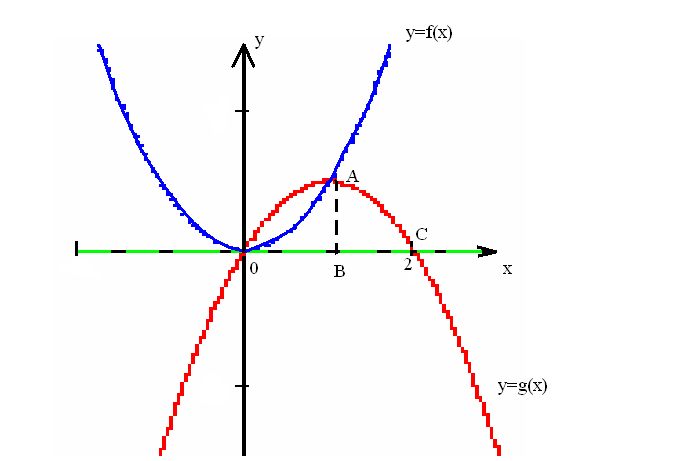 ешение 1.Выполним рисунок фигуры, площадь которой нужно найти.}

2. Найдем пределы интегрирования. Для этого решим уравнения: . и . 3. Вычислим площадь фигуры по формуле:

Ответ.