[Править] Ограничения корреляционного анализа

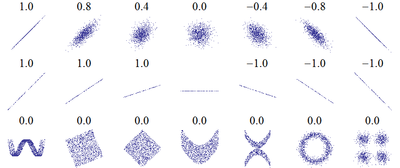
Множество корреляционных полей. Распределения значений (x, y) с соответствующими коэффициентами корреляций для каждого из них. Коэффициент корреляции отражает «зашумлённость» линейной зависимости (верхняя строка), но не описывает наклон линейной зависимости (средняя строка), и совсем не подходит для описания сложных, нелинейных зависимостей (нижняя строка). Для распределения, показанного в центре рисунка, коэффициент корреляции не определен, так как дисперсия y равна нулю.

1. Применение возможно при наличии достаточного количества наблюдений для изучения. На практике считается, что число наблюдений должно быть не менее, чем в 5-6 раз превышать число факторов (также встречается рекомендация использовать пропорцию не менее, чем в 10 раз превышающую количество факторов). В случае, если число наблюдений превышает количество факторов в десятки раз, в действие вступает закон больших чисел, который обеспечивает взаимопогашение случайных колебаний.^[13]

2. Необходимо, чтобы совокупность значений всех факторных и результативного признаков подчинялась многомерному нормальному распределению. В случае, если объём совокупности недостаточен для проведения формального тестирования на нормальность распределения, то закон распределения определяется визуально на основе корреляционного поля. Если в расположении точек на этом поле наблюдается линейная тенденция, то можно предположить, что совокупность исходных данных подчиняется нормальному закону распределения.^[14].

3. Исходная совокупность значений должна быть качественно однородной.^[13]

4. Сам по себе факт корреляционной зависимости не даёт основания утверждать, что одна из переменных предшествует или является причиной изменений, или то, что переменные вообще причинно связаны между собой, а не наблюдается действие третьего фактора.^[5]

] Область применения

Данный метод обработки статистических данных весьма популярен в экономике и социальных науках (в частности в психологии и социологии), хотя сфера применения коэффициентов корреляции обширна: контроль качества промышленной продукции, металловедение, агрохимия, гидробиология, биометрия и прочие. В различных прикладных отраслях приняты разные границы интервалов для оценки тесноты и значимости связи.

Популярность метода обусловлена двумя моментами: коэффициенты корреляции относительно просты в подсчете, их применение не требует специальной математической подготовки. В сочетании с простотой интерпретации, простота применения коэффициента привела к его широкому распространению в сфере анализа статистических данных.

Автокорреляция — статистическая взаимосвязь между случайными величинами из одного ряда, но взятых со сдвигом, например, для случайного процесса — со сдвигом по времени.

Автокорреляционная функция (АКФ, ACF).

В обработке сигналов автокорреляционная функция (АКФ) определяется интегралом:

и показывает связь сигнала (функции ) с копией самого себя, смещённого на величину .

В теории случайных функций АКФ является корреляционным моментом двух значений одной случайной функции :

Здесь , а — математическое ожидание.

График автокорреляционной функции можно получить, отложив по оси ординат коэффициент корреляции двух функций (базовой и функции сдвинутой на величину ) а по оси абсцисс величину . Если исходная функция строго периодическая, то на графике автокорреляционной функции тоже будет строго периодическая функция. Таким образом, из этого графика можно судить о периодичности базовой функции, а следовательно и о её частотных характеристиках. Это применяется для анализа сложных колебаний, например электроэнцефалограммы человека.

Содержание  [убрать]  1 Применение в технике 2 Другие применения 3 См. также 4 Ссылки