[Править] Непараметрические показатели корреляции [править] Коэффициент ранговой корреляции Кендалла
Применяется для выявления взаимосвязи между количественными или качественными показателями, если их можно ранжировать. Значения показателя X выставляют в порядке возрастания и присваивают им ранги. Ранжируют значения показателя Y и рассчитывают коэффициент корреляции Кендалла:
,
где
.
—
суммарное число наблюдений, следующих
за текущими наблюдениями с большим
значением рангов Y.
—
суммарное число наблюдений, следующих
за текущими наблюдениями с меньшим
значением рангов Y. (равные ранги не
учитываются!)
Если исследуемые данные повторяются (имеют одинаковые ранги), то в расчетах используется скорректированный коэффициент корреляции Кендалла:
—
число связанных рангов в ряду X и Y
соответственно.
[править] Коэффициент ранговой корреляции Спирмена
Каждому показателю X и Y присваивается
ранг. На основе полученных рангов
рассчитываются их разности
и
вычисляется коэффициент корреляции
Спирмена:
[править] Коэффициент корреляции знаков Фехнера
Подсчитывается количество совпадений и несовпадений знаков отклонений значений показателей от их среднего значения.
C — число пар, у которых знаки отклонений значений от их средних совпадают.
H — число пар, у которых знаки отклонений значений от их средних не совпадают.
[править] Коэффициент множественной ранговой корреляции (конкордации)
—
число групп, которые ранжируются.
—
число переменных.
—
ранг
-фактора
у
-единицы.
Значимость:
,
то гипотеза об отсутствии связи
отвергается.
В случае наличия связанных рангов:
[править] Свойства коэффициента корреляции
Неравенство Коши — Буняковского:
если принять в качестве скалярного
произведения двух случайных
величин ковариацию
,
то норма случайной величины будет равна
,
и следствием неравенства
Коши — Буняковского будет:
.
Коэффициент корреляции равен
тогда
и только тогда, когда
и
линейно
зависимы (исключая события нулевой
вероятности, когда несколько точек
«выбиваются» из прямой, отражающей
линейную зависимость случайных величин):
,
где
.
Более того в этом случае знаки
и
совпадают:
.
Доказательство [показать]
Рассмотрим
случайные величины X и Y c нулевыми
средними, и дисперсиями, равными,
соответственно,
и
.
Подсчитаем дисперсию случайной величины
:
Если предположить, что коэффициент корреляции
то предыдущее выражение перепишется в виде
Поскольку
всегда можно выбрать числа a и b так,
чтобы
(например,
если
,
то берём произвольное a и
),
то при этих a и b дисперсия
,
и значит
почти
наверное. Но это и означает линейную
зависимость между X и Y. Доказательство
очевидным образом обобщается на случай
величин X и Y с ненулевыми средними,
только в вышеприведённых выкладках
надо будет X заменить на
,
и Y — на
.
Если
независимые
случайные величины, то
.
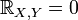Обратное в общем случае неверно.
[Править] Корреляционный анализ
Корреляционный анализ — метод обработки статистических данных, с помощью которого измеряется теснота связи между двумя или более переменными. Корреляционный анализ тесно связан с регрессионным анализом (также часто встречается термин «корреляционно-регрессионный анализ», который является более общим статистическим понятием), с его помощью определяют необходимость включения тех или иных факторов в уравнение множественной регрессии, а также оценивают полученное уравнение регрессии на соответствие выявленным связям (используя коэффициент детерминации).[1][2]