Регрессио́нный (линейный) анализ — статистический метод исследования влияния одной или нескольких независимых переменных на зависимую переменную . Независимые переменные иначе называют регрессорами или предикторами, а зависимые переменные — критериальными. Терминология зависимых и независимых переменных отражает лишь математическую зависимость переменных (см. Ложная корреляция), а не причинно-следственные отношения.

Содержание  [убрать]  1 Цели регрессионного анализа 2 Математическое определение регрессии 3 Метод наименьших квадратов (расчёт коэффициентов) 4 Интерпретация параметров регрессии 5 См. также 6 Ссылки 7 Литература

[Править] Цели регрессионного анализа

1. Определение степени детерминированности вариации критериальной (зависимой) переменной предикторами (независимыми переменными)

2. Предсказание значения зависимой переменной с помощью независимой(-ых)

3. Определение вклада отдельных независимых переменных в вариацию зависимой

Регрессионный анализ нельзя использовать для определения наличия связи между переменными, поскольку наличие такой связи и есть предпосылка для применения анализа.

[Править] Математическое определение регрессии

Строго регрессионную зависимость можно определить следующим образом. Пусть ,  — случайные величины с заданным совместным распределением вероятностей. Если для каждого набора значений определено условное математическое ожидание

(уравнение линейной регрессии в общем виде),

то функция называется регрессией величины Y по величинам , а её график — линией регрессии по , или уравнением регрессии.

Зависимость от проявляется в изменении средних значений Y при изменении . Хотя при каждом фиксированном наборе значений величина остаётся случайной величиной с определённым рассеянием.

Для выяснения вопроса, насколько точно регрессионный анализ оценивает изменение Y при изменении , используется средняя величина дисперсии Y при разных наборах значений (фактически речь идет о мере рассеяния зависимой переменной вокруг линии регрессии).

[Править] Метод наименьших квадратов (расчёт коэффициентов)

На практике линия регрессии чаще всего ищется в виде линейной функции (линейная регрессия), наилучшим образом приближающей искомую кривую. Делается это с помощью метода наименьших квадратов, когда минимизируется сумма квадратов отклонений реально наблюдаемых от их оценок (имеются в виду оценки с помощью прямой линии, претендующей на то, чтобы представлять искомую регрессионную зависимость):

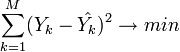
(M — объём выборки). Этот подход основан на том известном факте, что фигурирующая в приведённом выражении сумма принимает минимальное значение именно для того случая, когда .

Для решения задачи регрессионного анализа методом наименьших квадратов вводится понятие функции невязки:

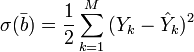
Условие минимума функции невязки:

Полученная система является системой линейных уравнений с неизвестными

Если представить свободные члены левой части уравнений матрицей

а коэффициенты при неизвестных в правой части матрицей

то получаем матричное уравнение: , которое легко решается методом Гаусса. Полученная матрица будет матрицей, содержащей коэффициенты уравнения линии регрессии:

Для получения наилучших оценок необходимо выполнение предпосылок МНК (условий Гаусса−Маркова). В англоязычной литературе такие оценки называются BLUE (Best Linear Unbiased Estimators) − наилучшие линейные несмещенные оценки.

[Править] Интерпретация параметров регрессии

Параметры являются частными коэффициентами корреляции; интерпретируется как доля дисперсии Y, объяснённая , при закреплении влияния остальных предикторов, то есть измеряет индивидуальный вклад в объяснение Y. В случае коррелирующих предикторов возникает проблема неопределённости в оценках, которые становятся зависимыми от порядка включения предикторов в модель. В таких случаях необходимо применение методов анализа корреляционного и пошагового регрессионного анализа.

Говоря о нелинейных моделях регрессионного анализа, важно обращать внимание на то, идет ли речь о нелинейности по независимым переменным (с формальной точки зрения легко сводящейся к линейной регрессии), или о нелинейности по оцениваемым параметрам (вызывающей серьёзные вычислительные трудности). При нелинейности первого вида с содержательной точки зрения важно выделять появление в модели членов вида , , свидетельствующее о наличии взаимодействий между признаками , и т. д (см. Мультиколлинеарность).

Корреля́ция (корреляционная зависимость) — статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин.^[1] Математической мерой корреляции двух случайных величин служит корреляционное отношение ^[2], либо коэффициент корреляции (или )^[1]. В случае, если изменение одной случайной величины не ведёт к закономерному изменению другой случайной величины, но приводит к изменению другой статистической характеристики данной случайной величины, то подобная связь не считается корреляционной, хотя и является статистической^[3].

Впервые в научный оборот термин «корреляция» ввёл французский палеонтолог Жорж Кювье в XVIII веке. Он разработал «закон корреляции» частей и органов живых существ, с помощью которого можно восстановить облик ископаемого животного, имея в распоряжении лишь часть его останков. В статистике слово «корреляция» первым стал использовать английский биолог и статистик Фрэнсис Гальтон в конце XIX века.^[4]

Некоторые виды коэффициентов корреляции могут быть положительными или отрицательными. В первом случае предполагается, что мы можем определить только наличие или отсутствие связи, а во втором — также и ее направление. Если предполагается, что на значениях переменных задано отношение строгого порядка, то отрицательная корреляция — корреляция, при которой увеличение одной переменной связано с уменьшением другой. При этом коэффициент корреляции будет отрицательным. Положительная корреляция в таких условиях — это такая связь, при которой увеличение одной переменной связано с увеличением другой переменной. Возможна также ситуация отсутствия статистической взаимосвязи — например, для независимых случайных величин.