2 Непрерывные случайные величины
Непрерывной
случайной величиной
(НСВ) называют переменную величину,
которая может принимать все значения
из некоторого промежутка. Так как
непрерывную случайную величину невозможно
задать с помощью закона распределения,
вводят функцию распределения. Функция
распределения
есть вероятность того, что случайная
величина примет значение, меньшее х,
то есть
.
Функция плотности
равна производной от функции
,
то есть
.
Функцию распределения называют интегральной функцией, а функцию плотности называют дифференциальной функцией.
Если известна функция , то можно найти по формуле
.
Вероятность попадания непрерывной случайной величины Х в интервал
можно вычислить,
используя функцию
,
по формуле
или, используя функцию , по формуле
.
Примечание. Так как для непрерывной случайной величины вероятность попадания в точку равна нулю, то
.
Если значения непрерывной случайной
величины заключены в интервале
,
то справедливы следующие формулы:
,
,
или
,
.
Пример 1. Непрерывная случайная величина Х задана функцией распределения
1) Построить график .
2) Найти функцию плотности и построить ее график.
3) Найти
:
а) используя функцию распределения ;
б) используя функцию плотности .
4) Найти вероятность
того, что в 100 независимых испытаниях
непрерывная случайная величина Х
хотя бы один раз попадет в интервал
.
5) Найти математическое ожидание случайной величины Х.
6) Найти дисперсию случайной величины Х:
а) по определению;
б) по «рабочей» формуле.
Решение. 1) График функции изображен на рисунке 9.
F(х)
F(х)
1
0 2 3 х
Рисунок 9
2) Запишем аналитическое выражение функции плотности :
График функции изображен на рисунке 10.
f (х)
2
f(х)
1
0 2 3 х
Рисунок 10
3а) Вычислим
вероятность попадания непрерывной
случайной величины Х
в интервал
,
используя функцию
,
по формуле
:
.
3б) Вычислим , используя плотность распределения:
.
4) Используем схему повторных независимых испытаний:
|
Искомую вероятность удобнее найти через вероятность противоположного события: |
|
|
,
,
Тогда
,
то есть попадание непрерывной случайной величины Х хотя бы один раз в интервал в 100 независимых испытаниях практически достоверно.
5) Математическое ожидание
6а) Найдем дисперсию, используя определение:
6б) Вычислим дисперсию по «рабочей» формуле:
7) Среднее квадратическое отклонение:
.
Пример 2. Непрерывная случайная величина Х задана функцией плотности :
Найти функцию распределения . Построить графики функций и .
Решение. 1) Используем
формулу
.
Так как подынтегральная функция
меняет свое аналитическое выражение,
то будем рассматривать х
на промежутках
,
и
(рисунок 11).
f
(х) 0 sin
x 0
0
х
Рисунок 11
1. Пусть
.
.
2. Пусть
.
3. Пусть
.
Запишем
аналитическое выражение для функции
:
2) Построим графики функций и .
f (х)
1 f (х)
0 х
Рисунок 12
F(х)
F(х)
1
0
х
Рисунок 13
Пример 3. Дан закон распределения дискретной случайной величины Х:
-
Х
–3
0
7
р
0,2
0,3
0,5
Найти – функцию распределения дискретной случайной величины Х. Построить ее график.
Решение. Используем определение функции : .
1. Пусть
(рисунок 14).
Х
х –3 0 7
Рисунок 14
Так как значений, меньших (–3), случайная величина не принимает, то
.
2. Пусть
(рисунок 15).
Х
–3 х 0 7
Рисунок 15
.
3. Пусть
(рисунок 16).
Х
–3 0 х 7
Рисунок 16
.
4. Пусть
(рисунок 17).
Х
–3 0 7 х
Рисунок 17
.
Запишем аналитическое выражение функции :
Изобразим график функции (рисунок 18).
F(x)
1
0,5
0,2
–3 0 7 х
Рисунок 18
Заметим, что в
точках разрыва величины скачков функции
0,2; 0,3; 0,5 равны соответственно
,
,
.
Пример 4. Задан график функции плотности непрерывной случайной величины Х (рисунок 19). Найти параметр С.
у
2
С х
Рисунок 19
Решение. По графику
функции плотности можно сделать вывод,
что все возможные значения непрерывной
случайной величины Х
заключены в интервале
.
Тогда
.
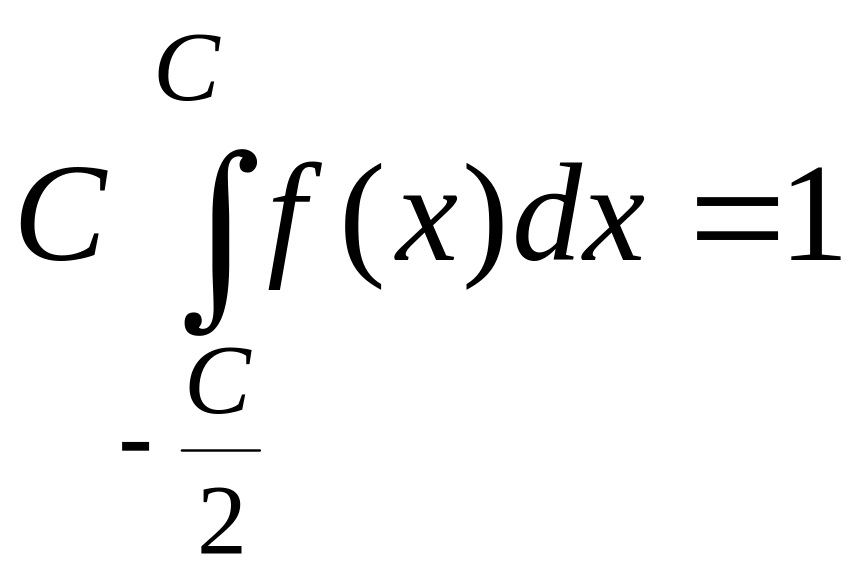Исходя из геометрического смысла определенного интеграла следует, что площадь фигуры, ограниченной функцией плотности и осью Ох, равна 1.
.
Отсюда
.