Нормальное распределение

Нормальное распределение – это совокупность объектов, в кото­рой крайние значения некоторого признака – наименьшее и наибольшее – появ­ляются редко; чем ближе значение признака к математическому ожиданию, тем чаще оно встречается.

Закон распределения вероятностей непрерывной случайной величины Х называется нормальным, если ее дифференциальная функция f(x) определяется формулой: где а совпадает с математическим ожиданием величины Х: а=М(Х), параметр  совпадает со средним квадратическим отклонением величины Х:  = (Х). Диаграмма нормального распределения симметрична относительно точки а (математического ожидания). Ме­диана, среднее арифметическое нормального распределения равны тоже а. При этом в точке а функция f(x) достигает своего максимума, который равен .

Пример 3: График плотности вероятности нормального распределения непрерывной величины X изображен на рисунке. Определите математическое ожидание, среднее квадратическое отклонение и максимальное значение дифференциальной функции распределения.

Решение.

П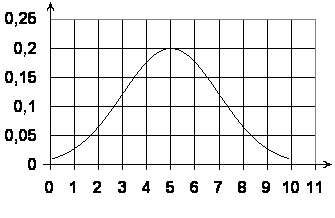 о графику можно найти максимальное значение дифференциальной функции распределения, оно составляет 0,2. Функция достигает максимума в точке x=5, следовательно, математическое ожидание M(X)=5. В точке максимума функция плотности вероятности примет вид: , следовательно,

В MS Excel для вычисления значений нормального распределения используются фун­кция НОРМРАСП, которая вычисляет значения вероятности нормальной функции распределения для указанного среднего и стандартного отклонения.

Функция имеет параметры:

НОРМРАСП (х; среднее; стандартное_откл; интегральная),

х – значения выборки, для которых строится распределение;

среднее – среднее арифметическое выборки;

стандартное_откл – стандартное отклонение распределения;

интегральная – логическое значение, определяющее форму функции. Если интегральная имеет значение ИСТИНА(1), то функция НОРМРАСП возвращает интег­ральную функцию распределения; если это аргумент имеет значение ЛОЖЬ (0), то вычисляется значение функции плотности распределения.

Если среднее = 0 и стандартное_откл = 1, то функция НОРМРАСП возвращает стан­дартное нормальное распределение.

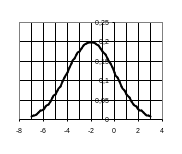
Пример 4: Составить дифференциальную функцию распределения непрерывной величины X, если известно, что величина распределена по нормальному закону с параметрами: математическое ожидание равно -2, а среднее квадратическое отклонение 2. Изобразить полученную функцию с помощью MS Excel.

Решение.

Дифференциальная функция распределения непрерывной величины X, распределенной по нормальному закону, имеет вид: 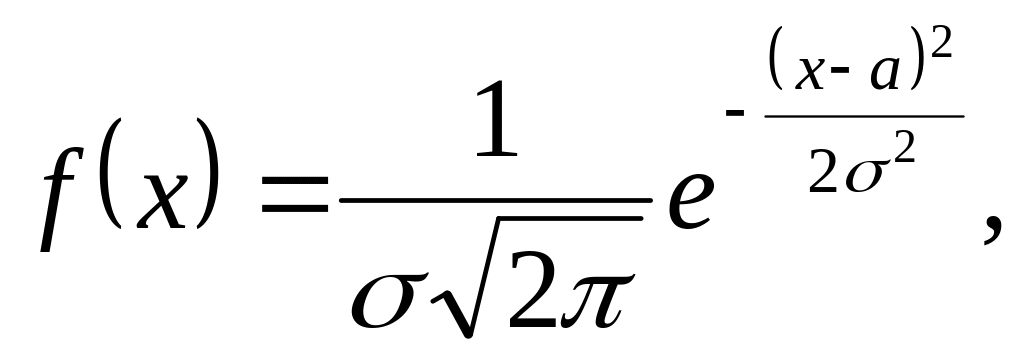где а – математическое ожидание;  – среднее квадратическое отклонение. По условию задачи математическое ожидание а=-2; среднее квадратическое отклонение =2, следовательно .

Для построения графика необходимо выбрать начальное значение для переменной x. Серединное значение совпадает с математическим ожиданием а, начальное значение отстоит от серединного не менее чем на , поэтому примем начальное значение x=-5. Запишем в ячейку A1 значение -5, в ячейку А2 – формулу =А1+0,2 и «протянем» эту формулу до ячейки А31, в которой получится значение 1. В ячейку B1 внесем формулу: =1/(2*КОРЕНЬ(2*ПИ()))*EXP(-((A1+2)^2)/8) и «протянем» эту формулу до ячейки В31. Выделяем ячейки в диапазоне А1:В31, выбираем Мастер диаграмм  Точечная диаграмма со значениями, соединенными сглаживающими линиями без маркеров, в результате получаем график плотности вероятности нормального распределения.

Пример 5: Построить график нормальной функции распределения f(x) при x, меняющемся от 19,8 до 28,8 с шагом 0,5, a=24,3 и =1,5.

Решение.

1. В ячейку А1 вводим символ случайной величины х, а в ячейку B1 – символ фун­кции плотности вероятности – f(x).

2. Вводим в диапазон А2:А21 значе­ния х от 19,8 до 28,8 с шагом 0,5. Для этого воспользуемся маркером автозаполнения: в ячейку А2 вводим левую границу диапазона (19,8), в ячейку A3 левую границу плюс шаг (20,3). Выделяем блок А2:А3. Затем за правый нижний угол протягиваем мышью до ячейки А21 (при нажатой левой кнопке мыши).

3. Устанавливаем табличный курсор в ячейку В2 и для получения значения веро­ятности воспользуемся специальной функцией — нажимаем на панели инстру­ментов кнопку Вставка функции f_x. В появившемся диалоговом окне Мастер функций – шаг 1 из 2 слева в поле Категория указаны виды функций. Выбираем Статистическая. Справа в поле Функция выбираем функцию НОРМРАСП. Нажимаем на кнопку ОК.

4. Появляется диалоговое окно НОРМРАСП. В рабочее поле X вводим адрес ячейки А2 щелчком мыши на этой ячейке. В рабочее поле Среднее вводим с клавиатуры значение математиче­ского ожидания (24,3). В рабочее поле Стандартное_откл вводим с клавиатуры значение среднеквадратического отклонения (1,5). В ра­бочее поле Интегральная вводим с клавиатуры вид функции распределения (0). Нажимаем на кнопку ОК.

5. В ячейке В2 появляется вероятность р = 0,002955. Указателем мыши за правый нижний угол табличного курсора протягиванием (при нажатой левой кнопке мыши) из ячейки В2 до В21 копируем функцию НОРМРАСП в диапазон В3:В21.

6. По полученным данным строим искомую диаграмму нормальной функции рас­пределения. Щелчком указателя мыши на кнопке на панели инструментов вызы­ваем Мастер диаграмм. В появившемся диалоговом окне выбираем тип диаграммы График, вид – развитие процесса по времени или по категориям.

После нажатия кнопки Далее указываем диапазон данных – В1:В21 (с помощью мыши). Проверяем, положение переключателя Ряды в: столбцах. Выбираем закладку Ряд и с помощью мыши вводим диапазон подписей оси X: А2:А21. Нажав на кнопку Далее, вводим названия осей Х, f(x) и нажимаем на кнопку Готово.

П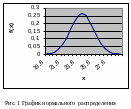 олучен приближенный график нормальной функции плотности распределения:

Задания для самостоятельного выполнения

Задание 1. Закон распределения случайной величины Х задан таблицей:

Х	0,2	0,4	0,6	0,8	1
Р	0,1	0,2	0,4	р4	0,1

Найдите p₄?

Задание 2. Закон распределения случайной величины Х задан таблицей:

Х	3	4	5	6	7
Р	р1	0,15	р3	0,25	0,35

Найдите вероятности р₁ р₃, если известно, что р₃ в 4 раза больше р₁?

Задание 3. Закон распределения случайной величины Х задан таблицей:

Х	2	3	5
р	0,3	0,1	0,6

Найдите М(Х) , D(X) и (Х).

Задание 4. В денежной лотерее выпущено 100 билетов. Разыгрываются 1 выигрыш в 500 руб. и 10 выигрышей по 100 руб. Найдите закон распределения случайного выигрыша Х для владельца одного лотерейного билета. Определите минимальную стоимость одного билета

5. При некоторых условиях стрельбы вероятность попадания в цель равна 0,8. Производится 10 выстрелов. Какова вероятность, что число попаданий в цель будет не менее двух?

6. Два равносильных противника играют в шахматы. Что вероятнее:

а) выиграть одну партию из двух или две партии из четырех?

б) выиграть не менее двух партий из четырех или не менее трех партий из пяти?

Задание 7. Известно, что непрерывная случайная величина распределена по нормальному закону, математическое ожидание равно 4. Определите значение среднего квадратического отклонения, если максимальное значение дифференциальной функции распределения составляет 0,4. Постройте график нормального распределения.

Задание 8. Известно, что непрерывная случайная величина распределена по нормированному закону, где х меняется от 10 до 20. Постройте график распределения.

Задание 9. Вероятность попадания в цель при стрельбе из орудия р = 0,6. Найдите математическое ожидание общего числа попаданий, если будет произведено 10 выстрелов.

Вопросы для самоконтроля

1. Чему равна сумма всех возможных вероятностей в законе распределения дискретной случайной величины?

1. Можно ли применять формулу Бернулли для зависимых испытаний?

2. Какими должны быть испытания, чтобы можно было применять формулу Бернулли?

3. Чему равно значение непрерывной случайной величины при котором функция плотности вероятности этой величины достигает максимального значения?

5. Приведите пример непрерывной случайной величины, распределенной по нормальному закону?

6. Как найти вероятность того, что в n независимых испытаниях событие A появится хотя бы один раз?

Математическая статистика

Основные умения: рассчитывать основные статистические показатели для решения профессиональных задач; осуществлять самостоятельную деятельность по сбору, обработке, группировке, анализу информации; использовать методы математической статистики в психолого-педагогических исследованиях.

Основной величиной в статистических измерениях является единица статистической совокупности (например, любой из критериев оценки качества педагога-исследователя). Единица статистической совокупности характеризуется набором признаков или параметров. Значения каждого параметра или признака могут быть различными и в целом образовывать ряд случайных значений x₁, х₂, …, х_n.

Переменная (variable) – это параметр измерения, который можно контролировать или которым можно манипулировать в исследовании. Так как значения переменных не постоянны, нужно научиться описывать их изменчивость.

Для этого придуманы описательные или дескриптивные статистики: минимум, максимум, среднее, дисперсия, стандартное отклонение, медиана, квартили, мода.

Относительное значение параметра – это отношение числа объектов, имеющих этот показатель, к величине выборки. Выражается относительным числом или в процентах (процентное значение).

Пример 1: Успеваемость в классе = числу положительных итоговых отметок, деленному на число всех учащихся класса. Умножение этого значения на 100 дает успеваемость в процентах. 25/100=25%

Удельное значение данного признака – это расчетная величина, показывающая количество объектов с данным показателем, которое содержалось бы в условной выборке, состоящей из 10, 100, 1000 и т. д. объектов.

Пример 2: Для сравнения уровня правонарушений в разных регионах берется удельная величина – количество правонарушений на 1000 человек (N).

Минимум и максимум – это минимальное и максимальное значения перемен­ной.

Размах (R) – это разность между максимальным и минимальным значением переменной: R= max–min.

Среднее арифметическое может вычисляться как по необработанным первичным данным, так и по результатам группировки этих данных.

Для несгруппированных данных:

(1)

где n – объем выборки; x_i – значения выборки.

Для сгруппированных данных:

(2)

где n – объем выборки; k – число интервалов группировки; n_i – частоты интервалов; x_i – срединные значения интервалов.

Пример 3: Наблюдение посещаемости четырех внеклассных мероприятий в экспериментальном (20 учащихся) и контрольном (30) классах дали значения (соответственно): 18, 20, 20, 18 и 15, 23, 10, 28. Среднее значение посещаемости в обоих классах получается одинаковое – 19. Однако видно, что в контрольном классе этот показатель подчинен воздействию каких-то специфических факторов.

Медианой (Ме) называется такое значение признака X, когда одна половина значений экспериментальных данных меньше ее, а вто­рая половина – больше.

Для вычисления медианы несгруппированных данных выборку сортируют, находят ранг R (порядковый номер) медианы:

(3)

Медианой будет значение признака, стоящее на R_Ме месте в ранжированной выборке. Для нахождения медианы в случае сгруппированных данных:

(4)

где х_MeН – нижняя граница медианного интервала; h – ширина ин­тервалов группировки; n_xMe–1 – накопленная частота интервала, предшествующего медианному; n_Me – частота медианного интервала.

Мода (Мо) представляет собой значение признака, встречающего­ся в выборке наиболее часто.

Если распределение имеет несколько мод, то говорят, что оно мультимодально или многомодально (имеет два или более «пика»). Для несгруппированных данных мода – это значение признака с наибольшей частотой появления.

Для сгруппированных данных:

(5)

где x_MoH – нижняя граница модального интервала, n_Mo – частота интервала.

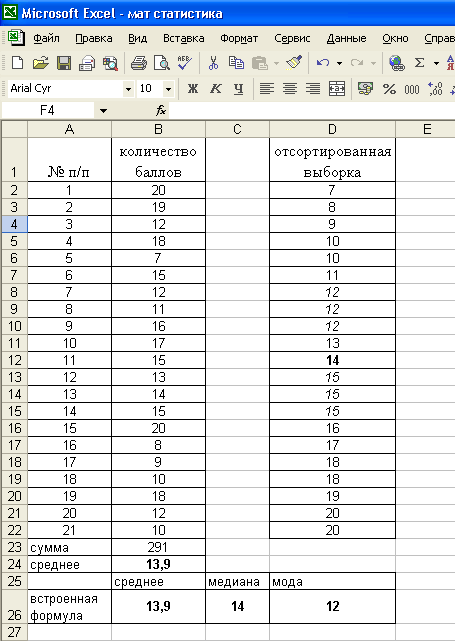
Пример 4: Найти среднее арифметическое, моду и медиану распределения студентов по числу баллов, полученных ими на экзамене: 20 19 12 18 7 15 12 11 16 17 15 13 14 15 20 8 9 10 18 12 10.

Решение.

Решим данную задачу, используя электронные таблицы MS Excel.

Внесите данные задачи в столбец В листа электронных таблиц, начиная со второй строки. В столбец А внесите № п/п, проставив которые получим последний №, соответствующий объему выборки n=21.

Поставив курсор в ячейку В23 введем формулу нахождения среднего значения =СРЗНАЧ(В2:В22). Можно ввести собственную формулу: =СУММ(В2:В22)/21.

Для вычисления медианы, расположим данные в порядке возрастания: скопируем данные в столбец D, выделим столбец и отсортируем. Найдем ранг медианы по формуле (3): На 11-м месте в ранжированной выборке стоит значение 14. Ме=14. Используя встроенную функцию: =МЕДИНА(В2:В22), получаем то же значение 14.

Для нахождения моды воспользуемся ранжированной выборкой, в которой можно заметить, что наиболее часто (3 раза) встречаются значения 12 и 15 – значения несмежные, поэтому выборка имеет 2 моды и называется бимодальной. Используя встроенную функцию: =МОДА (В2:В22). Получаем значение 12 (Excel не рассматривает случаи бимодальных распределений).

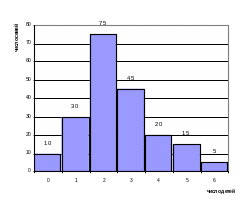
Пример 5: Дано распределение семей по числу детей. Найти моду, медиану и среднее арифметическое. Построить гистограмму и полигон распределения.

Число детей	0	1	2	3	4	5	6
Число семей	10	30	75	45	20	15	5

Решение. Значением признака будет являться число детей, а частотой – число семей, в которых содержится такое количество детей. Найдем среднее арифметическое количества детей в семье.

Внесем таблицу на лист электронных таблиц: число детей – в столбец А; число семей в столбец В. Данные в таблице являются сгруппированными.

Н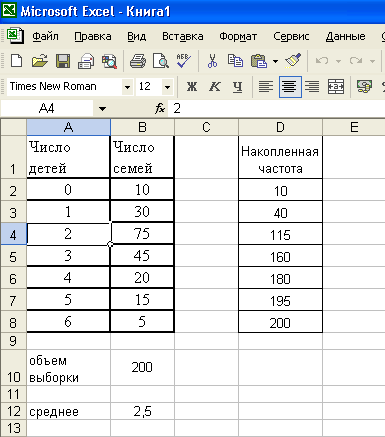 айдем общий объем выборки, суммируя данные столбца числа семей, и занесем в ячейку В10 формулу =СУММ(В2:В8), получим n=200. Для нахождения значения среднего арифметического сгруппированных данных воспользоваться встроенной функции невозможно, поэтому применяем формулу (2) – сумма произведений значений столбцов А и В =СУММПРОИЗВ(A2:A8;B2:B8)/B10 и занесем формулу в ячейку В12, получим .

Для нахождения медианы необходимо определить медианный интервал. Медианным будет тот интервал, в котором накопленная частота впервые окажется больше n/2 (n/2=200/2=100). В столбец D занесем значения накопленных частот: в D2 – В2, в D3=D2+B3 и т.д. Замечаем, что накопленная частота больше 100 равная 115 соответствует значению признака 2 ребенка в семье. Ме=2.

Мо=2, т.к. это значение признака встречается наиболее часто – 75 раз.

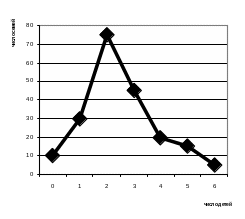
Построим гистограмму:				Построим полигон:

Для оценки степени разброса (отклонения) какого-то показателя от его среднего значения, наряду с максимальным и минимальным значениями, используются понятия дисперсии и стандартного отклонения.

Дисперсия выборки или выборочная дисперсия (от английского variance) – это мера изменчивости переменной. Термин впервые введен Фишером в 1918 году.

Дисперсия меняется от нуля до бесконечности. Крайнее значение 0 означает отсутствие изменчивости, когда значения переменной постоянны.

Стандартное отклонение, среднее квадратическое отклонение (от английского standard deviation) вычисляется как корень квадратный из дисперсии. Чем выше дисперсия или стандартное отклонение, тем сильнее разбросаны значения переменной относительно среднего.

Пример 7: По данным примера 3, где приводиится посещаемость четырех внеклассных мероприятий в экспериментальном (20 учащихся) и контрольном (30) классах, рассчитаем дисперсию и стандартное отклонение:

Классы		D(x)
Экспериментальный	19	1	1
Контрольный	19	48,5	8

Это означает, что в одном классе посещаемость высокая, стабильная, а в другом – отличается непостоянством.

Задания для самостоятельного выполнения

Задание 1. Найти среднее арифметическое, моду и медиану распределения абитуриентов по числу баллов, полученных ими на экзамене: 80 69 72 44 51 38 62

Задание 2. Рассчитать описательную статистику для следующего распределения температуры тела больных в изоляторе за день: 38 40 37 38 38 40 37 37 38 38 37 39 38 39 38 39 37. Построить дискретный вариационный ряд и гистограмму, начертить полигон частот.

Задание 3. По результатам исследования на вопрос анкеты: «укажите степень владения иностранным языком», ответы распределились следующим образом:

1 – владею свободно – 25

2 – владею в достаточной степени для общения – 50

3 – владею, но испытываю трудности при общении – 250

4 – понимаю с трудом – 170

5 – не владею – 10

Найти среднее значение, медиану и моду выборки. Постройте гистограмму и полигон частот по имеющимся данным. Сделайте вывод.

Задание 4. Педагог-исследователь провел тестирование интеллекта по тесту Векслера у 20 школьников и получил следующие данные: 6, 9, 5, 7, 10, 8, 9, 10, 8, 11, 9, 12, 9, 8, 10, 11, 9, 10, 8, 10. Отсортируйте полученные данные по убыванию, рассчитайте среднее значение, моду, медиану, эксцесс и ассиметрию выборки.

Вопросы для самоконтроля

1. В каких случаях применяется аппарат математической статистики?

1. Для чего предназначен раздел математической статистики: описательная статистика?

1. Как характеризует распределение выборки стандартное отклонение, ассиметрия и эксцесс?

2. В каких случаях необходим аппарат математической статистики в деятельности педагога?