3.3. Изотермический процесс
При изотермическом процессе температура постоянна, следовательно,
(20)
или
(21)
т.е. давление и объем обратно пропорциональны друг другу, так что при изотермическом сжатии давление газа возрастает, а при расширении падает.
Первое начало термодинамики для этого процесса будет иметь вид
(22)
или
(23)
Также первое начало термодинамики для изотермического процесса можно представить в виде
(24)
или
(25)
С учетом выражений (20) и (23) можно записать дифференциал удельной энтропии
.
(26)
В интегральной форме первое начало термодинамики для изотермического процесса будет иметь вид
(27)
или
.
(28)
Из выражений (20) ─
(28) следует, что для изотермического
процесса идеального газа
или
основные расчетные формулы примут вид:
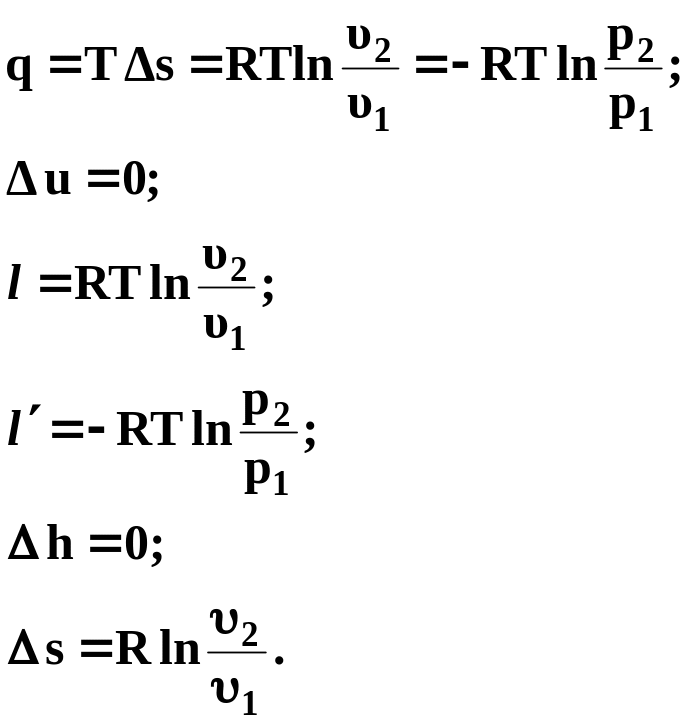(29)
Графиком изотермического процесса в ─ координатах является равнобокая гипербола, для которой координатные оси служат асимптотами (рисунок 3).
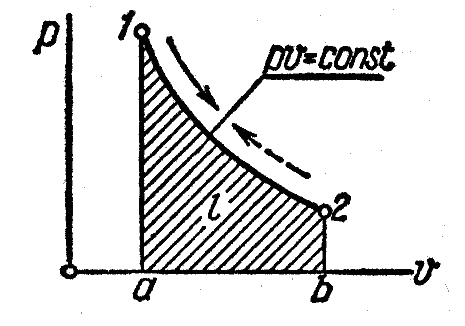
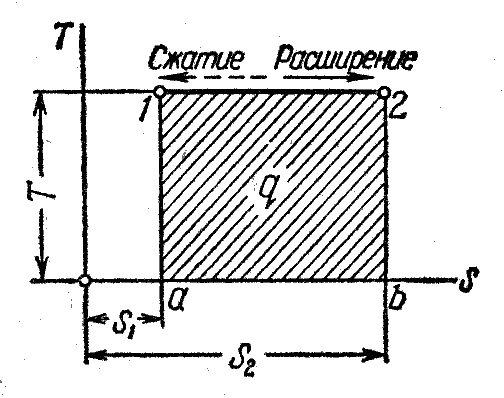
Рисунок 3 ─ Изображение изотермического процесса в и ─координатах
3.4. Адиабатный процесс
Процесс, происходящий
без теплообмена с окружающей средой,
называется адиабатным,
т.е.
.
Это процесс
называется также изоэнтропным,
так как
.
Первое начало термодинамики для адиабатного процесса будет иметь вид
(30)
или с учетом выражений
и
(31)
С учетом выражений
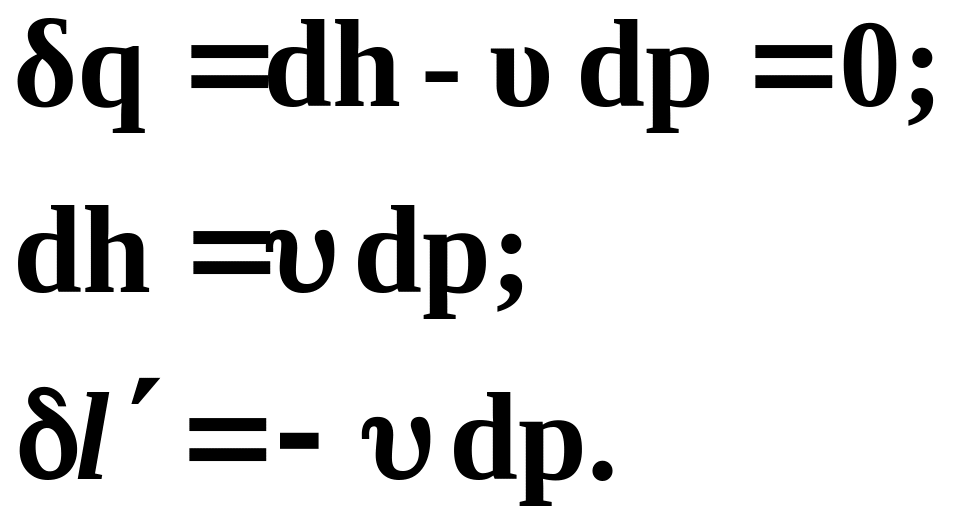
первое начало термодинамики для изобарного процесса можно представить в виде
(32)
или
(33)
Из выражения (31) найдем уравнение адиабатного процесса
(34)
Дифференцируя уравнение состояния идеального газа
,
(35)
Подставляя полученное выражение в уравнение (34), получим
(36)
С учетом формулы Майера, получим
или
(37)
Разделив уравнение
(37) на
,
получим
Обозначим отношение
где
показатель адиабаты.
Тогда
(38)
Проинтегрируем выражение (38)
(39)
или
.
(40)
Если логарифм некоторой функции есть величина постоянная, то и сама функция является постоянной величиной
(41)
Выражение (41) представляет собой уравнение адиабатного процесса.
В интегральной будет иметь вид форме первое начало термодинамики для адиабатного процесса
(42)
или
(43)
Из уравнений (30) ─
(42) следует, что для адиабатного процесса
идеального газа
:
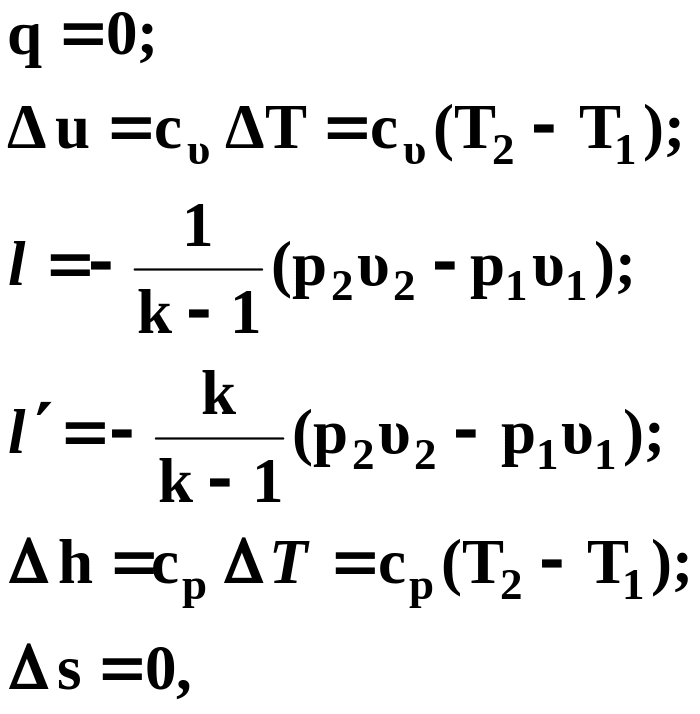(44)
где
начальная и конечная температура газа
в процессе соответственно;
начальный и конечный удельный объем
газа в процессе;
начальное и конечное давление газа в
процессе.
На рисунке 4 представлено изображение адиабатного процесса и ─ координатах.
Поскольку
,
то в координатах
линия адиабаты идет круче линии изотермы:
при адиабатном
расширении давление понижается быстрее,
чем при изотермическом, так как в процессе
расширения уменьшается температура
газа.
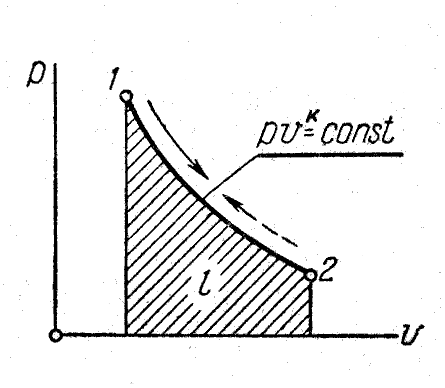
Рис. 4. Изображение адиабатного процесса в и ─ координатах