Классификация цепей и сетей.

Сети общего назначения: электроснабжение бытовых, промышленных, сельскохозяйственных и транспортных потребителей.

Сети автономного электроснабжения: электроснабжение мобильных и автономных объектов (транспортные средства, суда, самолёты, космические аппараты, автономные станции, роботы и т. п.)

Сети технологических объектов: электроснабжение производственных объектов и других инженерных сетей.

Контактная сеть: специальная сеть, служащая для передачи электроэнергии на движущиеся вдоль неё транспортные средства (локомотив, трамвай,троллейбус, метро).

Масштабные признаки, размеры сети

Магистральные сети: сети, связывающие отдельные регионы, страны и их крупнейшие источники и центры потребления. Характерны сверхвысоким и высоким уровнем напряжения и большими потоками мощности (гигаватты).

Региональные сети: сети масштаба региона (в России - уровня субъектов Федерации). Имеют питание от магистральных сетей и собственных региональных источников питания, обслуживают крупных потребителей (город, район, предприятие, месторождение, транспортный терминал). Характерны высоким и средним уровнем напряжения и большими потоками мощности (сотни мегаватт, гигаватты).

Районные сети, распределительные сети. Имеют питание от региональных сетей. Обычно не имеют собственных источников питания, обслуживают средних и мелких потребителей (внутриквартальные и поселковые сети, предприятия, небольшие месторождения, транспортные узлы). Характерны средним и низким уровнем напряжения и небольшими потоками мощности (мегаватты).

Внутренние сети: распределяют электроэнергию на небольшом пространстве — в рамках района города, села, квартала, завода. Зачастую имеют всего 1 или 2 точки питания от внешней сети. При этом иногда имеют собственный резервный источник питания. Характерны низким уровнем напряжения и небольшими потоками мощности (сотни киловатт, мегаватты).

Электропроводка: сети самого нижнего уровня — отдельного здания, цеха, помещения. Зачастую рассматриваются совместно с внутренними сетями. Характерны низким и бытовым уровнем напряжения и маленькими потоками мощности (десятки и сотни киловатт).

Уравнение состояние проводов при различных климатических условиях

При разных атмосферных условиях в проводах будут возникать разные напряжения, а следовательно, будут разные стрелы провеса.

Нам нужно определить наибольшую стрелу провеса.

Пусть есть «m»-ные климатические условия с характеристиками: 

Тогда 

Предположим, климатические условия изменились. Стали какими-то «n»-ные условия:  В этом случае:

 

.    Длину провода в пролёте можно определить при «n»-ных условиях, зная   Мы можем записать  в этом выражении подставим   и  .

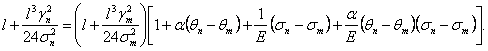
Получено сложное уравнение третьего порядка. Принимают, что последним членом в квадратных скобках можно пренебречь, ( =23·10^-6;  =6300) – как пример для алюминия.

Оставшееся уравнение преобразуем:

 Запишем это выражение более удобно. Примем, что « » отличается от « » на 2…3%. Таким образом, можно « » заменить на « ». Каждый член уравнения разделим на « ». При перенесении членов из левой части в правую все знаки будем менять на обратные.

 - уравнение состояния провода (основное расчётное уравнение).

Это кубическое уравнение   - решается чаще всего методом подбора, (это раньше, сейчас, на ЭВМ, методом половинного деления и другими).

Расчёт по этому уравнению можно проводить и для монометаллических и комбинированных проводов. Для комбинированных проводов в расчётное уравнение подставляются величины, характеризующие провод в целом ( ;   и другие).

Таким образом, имея уравнение состояния провода, зная напряжения при «m»-ных условиях, мы можем найти напряжения в материале провода при любых атмосферных условиях.

Вопрос в том, какое напряжение является исходным. Отправной точкой будут являться допускаемые напряжения. При любых условиях напряжения в материале провода не должно быть больше допускаемой величины. Мы имеем три допускаемых напряжения, нужно определить которое нам нужно.

 

определение потерь напряжения в линиях с двухсторонним питанием

Рассмотрим методику расчета линий с двусторонним питанием, являющуюся общим случаем расчета простых замкнутых сетей, поскольку, кольцевая сеть легко приводится к схеме двустороннего питания. Схема такой сети для трех нагрузок изображена на рис. 7-4. Здесь s₁,s₂ и s₃ — нагрузки в точках 1, 2 и 3;S₁, S₂, S₃ и S₄ — полные мощности на участках линии; Z_0-1, Z_1-2, Z_2-3 и Z_3-4, l₁, l₂, l₃, и l₄ — соответственно полные сопротивления и длины участков; А и В — источники питания; U_A и U_B — напряжения источников питания.

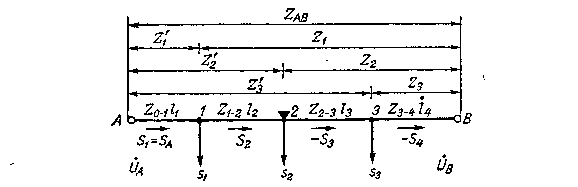
Рис. 7-4. Схема сети с двусторонним питанием.

Падение линейного напряжения на любом участке линии между нагрузками

где Ii — ток на данном участке; Zi — сопротивление этого участка.

Поскольку

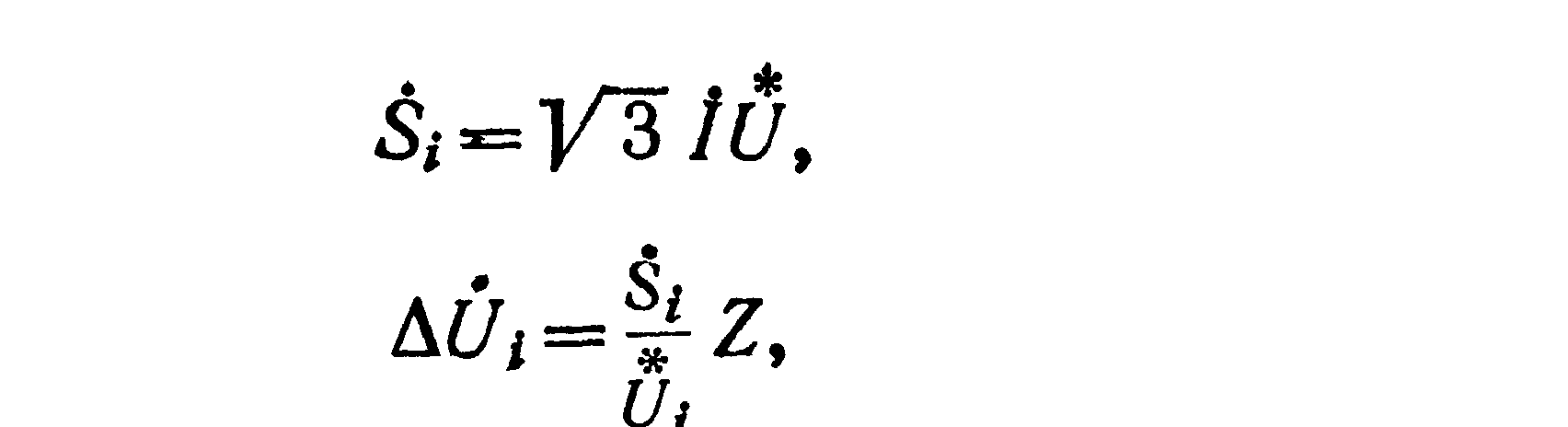
где Ui — сопряженный вектор напряжения в данной точке сети.

Полагая вектор Ui ориентированным по вещественной оси, получим:

где Si и Ui взяты для одной и той же точки участка.

Вектор напряжения Ui изменяется вдоль линии по мере удаления от источника питания. Однако, пренебрегая потерями мощности в линии, т. е. исходя из постоянства напряжения вдоль каждого участка и полагая U₁ = U₂ = ... = U_N (что для сетей местного значения вполне допустимо), можем на основании второго закона Кирхгофа написать следующее равенство для падений напряжения между точками А и В:

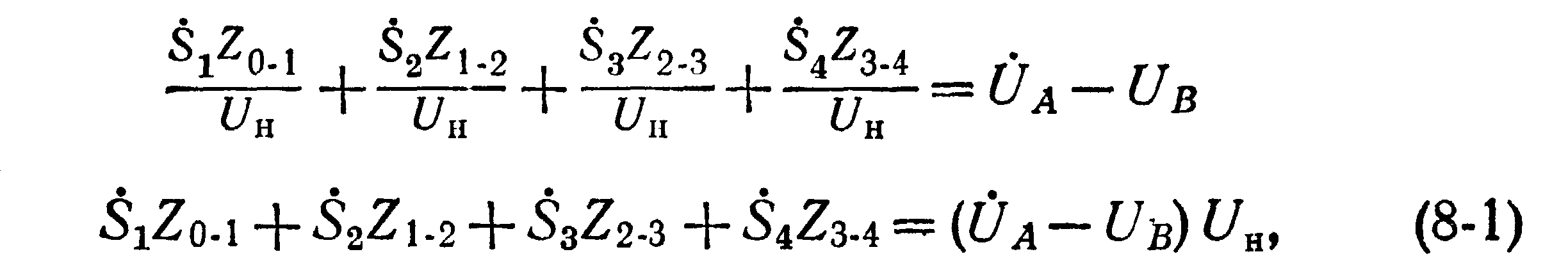
где Uн — номинальное напряжение сети.

Одновременно, пользуясь первым законом Кирхгофа для точек 1, 2, 3 и исходя из принятого допущения об отсутствии потерь мощности в сети, можно составить следующие равенства:

Подставив эти выражения в уравнение (8-1), получим:

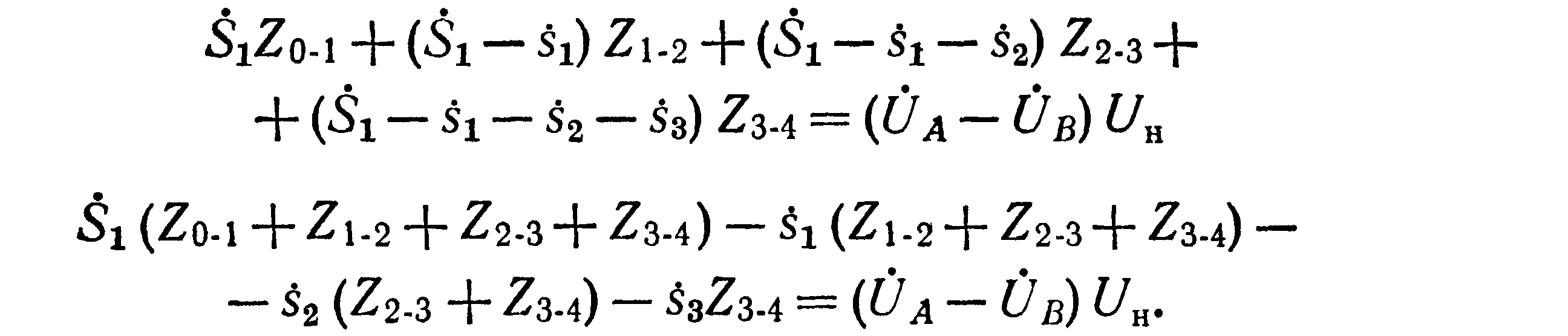
Отсюда искомая мощность, выходящая в линию из пункта А, будет

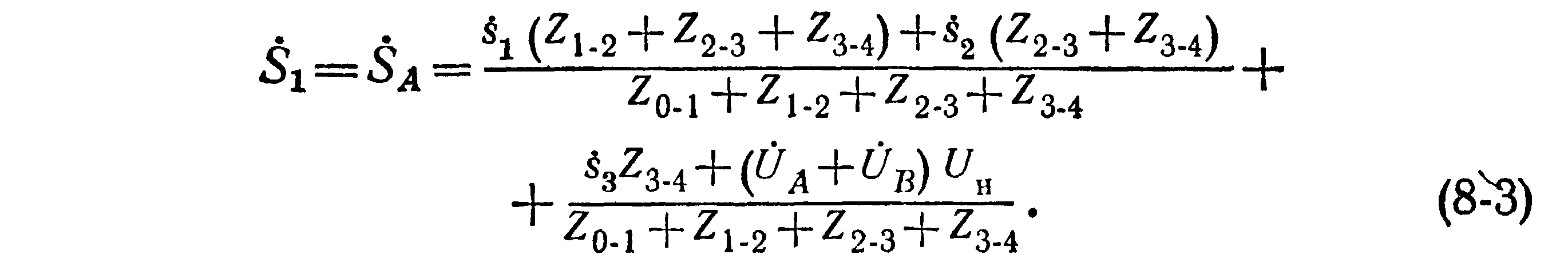
Ф ГАОУ ВПО «Северо-восточный Федеральный университет им. М. К. Аммосова»

Физико-технический институт

Кафедра «Теплофизики и теплоэнергетики»