4.2. Фінансові розрахунки вартості грошей.

 

Досконале володіння основами фінансової математики дозволяє порівнювати між собою ефективність окремих операцій і обґрунтовувати найбільш оптимальні управлінські рішення.

Широке поширення одержало використання фінансових таблиць для нарахування складних процентів і дисконтування. У цих таблицях приводяться значення множників нарощення (дисконтних множників) для заданих n та і. Для перебування нарощеної вартості досить помножити відому первісну суму на табличне значення множника нарощення. Аналогічно можна знайти приведену величину майбутніх грошей, множачи їх суму на дисконтний множник з таблиці. Розглянемо деякі інші елементарні способи використання результатів фінансових обчислень.

В умовах нестабільної економіки банки й інші кредитори з метою зниження свого процентного ризику можуть установлювати перемінні ставки процентів для різних фінансових операцій.

Наприклад, по позичці в розмірі 2 млн. грн. загальною тривалістю 120 днів протягом перших двох місяців будуть нараховуватися 20% річних, а починаючи з 61 дня щомісяця проста процентна ставка буде збільшуватися на 3% (звичайні проценти). Фактично, позичка розбивається на декілька складових, по кожній з яких установлені свої умови. Необхідно знайти нарощені суми по кожній зі складових, а потім скласти їх. При нарахуванні простих процентів варто говорити про базисні темпи приросту, тому що первісна сума P залишається незмінною. Дана задача в статистичних термінах може бути інтерпретована як додавання базисних темпів приросту з наступним множенням на первісну суму позики. Загальна формула розрахунку буде мати такий вигляд:

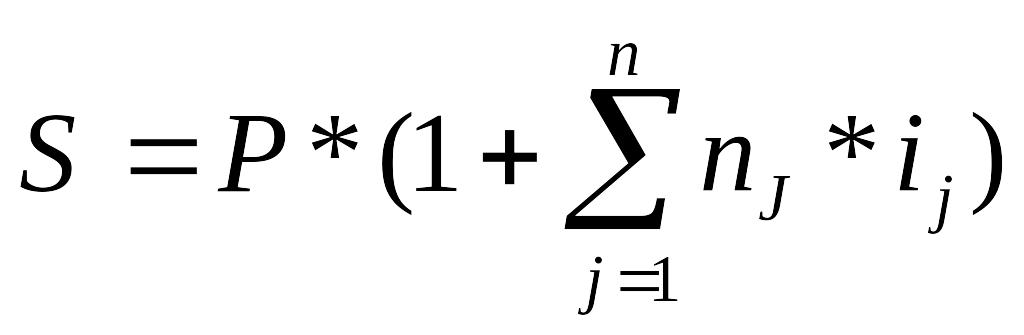  , (4.18)

де N - загальне число періодів, протягом яких проценти нараховуються по незмінній ставці. Підставивши в це вираження умови нашого приклада, отримаємо:

S = 2 * (1 + (60/ 360 * 0,2) + (30/ 360 * 0,23) + (30/360 * 0,26)) = 2,148 млн. грн.

Відповідно для складних процентів, мова йтиме вже не про базисні, а про ланцюгові темпи приросту, що повинні не складатися, а перемножуватися:

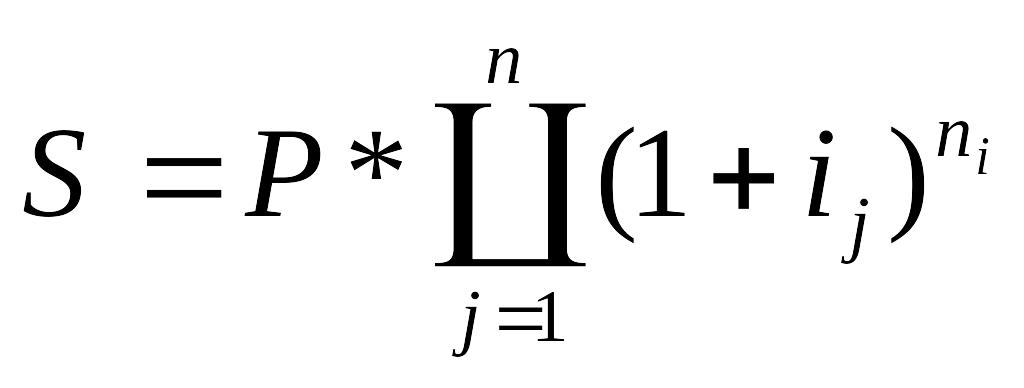  . (4.19)

Підставивши умови приклада, отримаємо:

S = 2 * (1 + 0,2)^(60/360) * (1 + 0,23)^30/360 * (1 + 0,26)^30/360 = 2,138 млн. грн.

Дану задачу можна вирішити трохи іншим шляхом – розрахувавши спочатку середні процентні ставки. Розрахунок середніх процентних ставок (чи розрахунок середніх доходностей) узагалі дуже розповсюджений у фінансових операціях. Для його виконання корисно знову згадати про математико-статистичну природу процентних ставок, тому що нарахування простих процентів відбувається в арифметичній прогресії, середня проста ставка розраховується як середня арифметична зважена

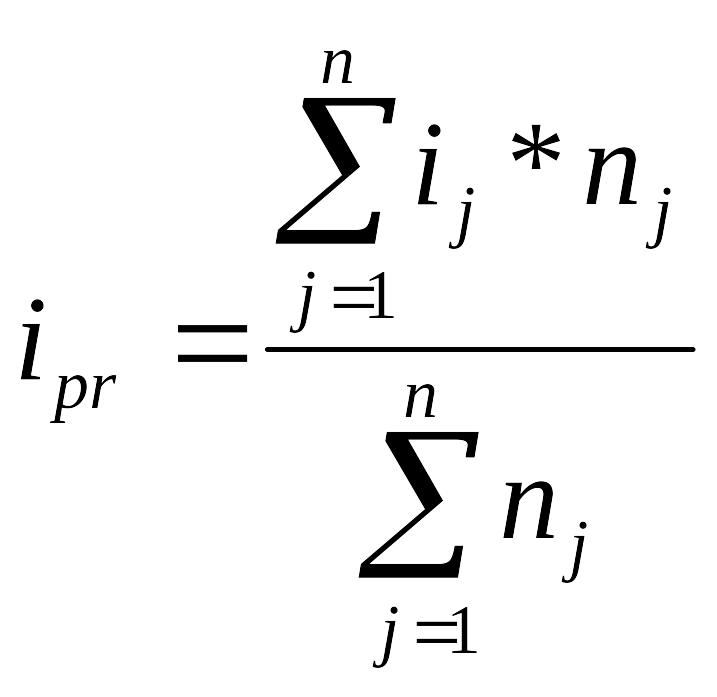, (4.20)

де N – загальне число періодів, протягом яких процентна ставка залишалася незмінною.

Складні проценти ростуть у геометричній прогресії, тому середня складна процентна ставка розраховується як середня геометрична зважена. У якості ваги в обох випадках використовуються тривалості періодів, для яких діяла фіксована ставка.

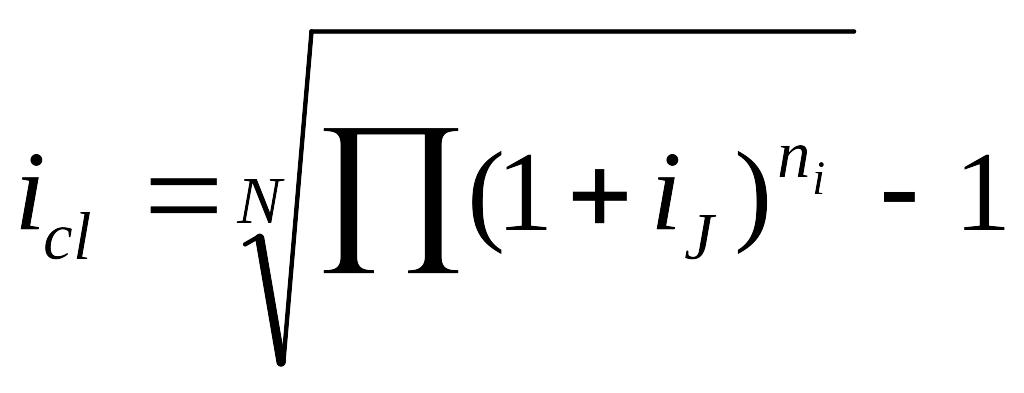. (4.21)

Знову використовуємо дані нашого приклада. У випадку нарахування простих процентів отримаємо:

= ((0,2 * 60) + (0,23 * 30) + (0,26 * 30)) / 120 = 0,223 = 22,3%

S = 2 * (1 + 0,223 * 120 / 360) = 2,149 млн. грн.

Тобто середня процентна ставка склала 22,3% і нарахування процентів по цій ставці за весь термін позички дає такий же результат, як і той, що був отриманий по формулі (4.21). Для складних процентів вираження прийме вигляд:

= ((1 + 0,2)^60 * (1 + 0,23)^30 * (1 + 0,26)^30)^(1/120) – 1 = 0,222 = 22,2%

S = 2 * (1 + 0,222)^(120/360) = 2,138 млн. грн.

Нарахування процентів по середній процентній ставці 22.2% також дає результат, еквівалентний тому, що був отриманий по формулі (4.22).

Розуміння розходжень механізмів нарощення простих і складних процентів допомагає уникати досить розповсюджених помилок. Наприклад, варто пам'ятати, що такий процес, як інфляція розвивається в геометричній, а не в арифметичній прогресії, тобто до нього повинні застосовуватися правила нарахування складних, а не простих процентів. Темпи приросту цін у цьому випадку являються ланцюговими, а не базисними, тому що в кожному наступному місяці ріст цін відноситься до попереднього місяцю, а не до початкового року чи якій-небудь інший незмінній базі.

Поряд з розрахунком майбутньої і сучасної величини коштів часто виникають задачі визначення інших параметрів фінансових операцій: їх тривалості і величини процентної чи дисконтної ставок.

Визначення терміну фінансової операції для антисипативного нарахування процентів і банківського обліку здійснюється по формулі (4.24) з табл. 4.1.

Наприклад, через який період часу відбудеться подвоєння суми боргу при нарахуванні на неї 20% річних простих

а) при декурсивному методі нарахування процентів;

б) при використанні антисипативного методу.

Тимчасова база в обох випадках приймається рівною 365 днів (точні проценти).

Розв’язання

Застосувавши формули (4.22) і (4.23), отримаємо:

а) t = (2 – 1) / 0,2 * 365 = 1825 днів (5 років);

б) t = (1 – 1/2) / 0,2 * 365 = 912,5 днів (2,5 роки).

Наприклад, за векселем номіналом 700 тис. грн. банк виплатив 520 тис. грн., зробивши його облік по простій ставці 12% річних.

Чому дорівнює термін до погашення векселя?

Розв’язання

Застосувавши формулу (4.2.5), отримаємо:

t = (1 – 520 / 700) / 0,12 * 360 = 771 день.

Наприклад/

Товар, вартістю 1,5 млн. грн. оплачується на умовах комерційного кредиту, наданого під 15% річних (проста процентна ставка, тимчасова база 360 днів). Сума оплати після закінчення терміну кредиту склала 1 млн. 650 тис. грн.

Чому дорівнює термін наданого кредиту?

Розв’язання

З формули (4.21) випливає:

t = (1,65/1,5 – 1) / 0,15 * 360 = 240 днів.

Таблиця 4.1.

Формули розрахунку тривалості фінансових операцій і процентних (облікових) ставок по них

Спосіб нарахування процентів	Тривалість позички	Процентна (облікова) ставка
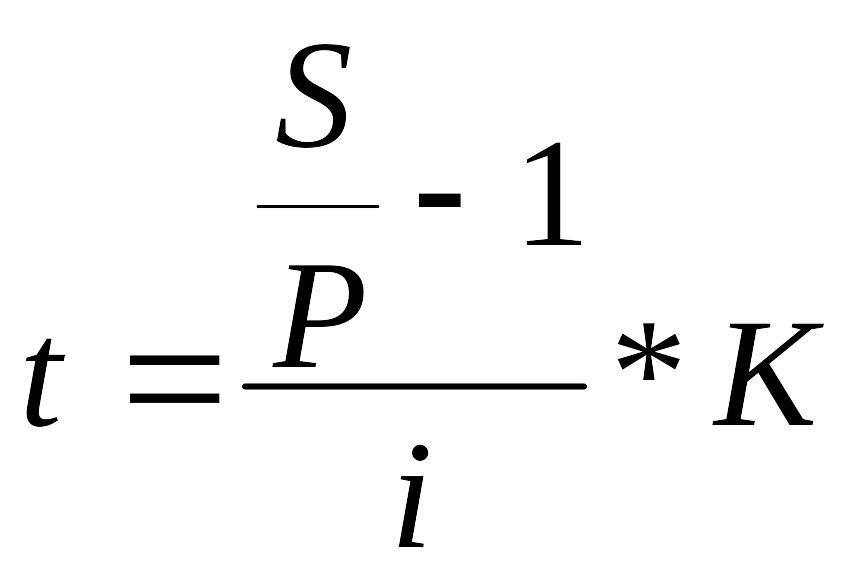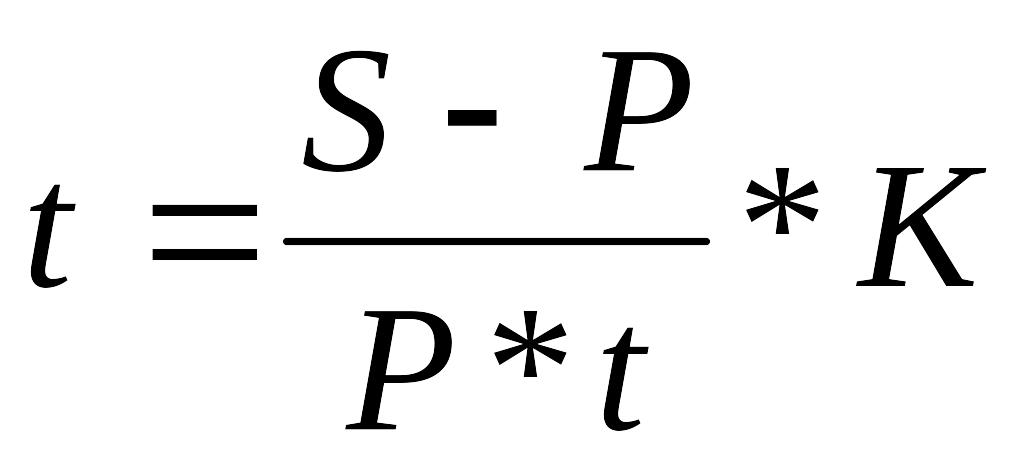1. Прості декурсивні проценти (t – тривалість у днях, K – тимчасова база)	; (4.22)	; (4.24)
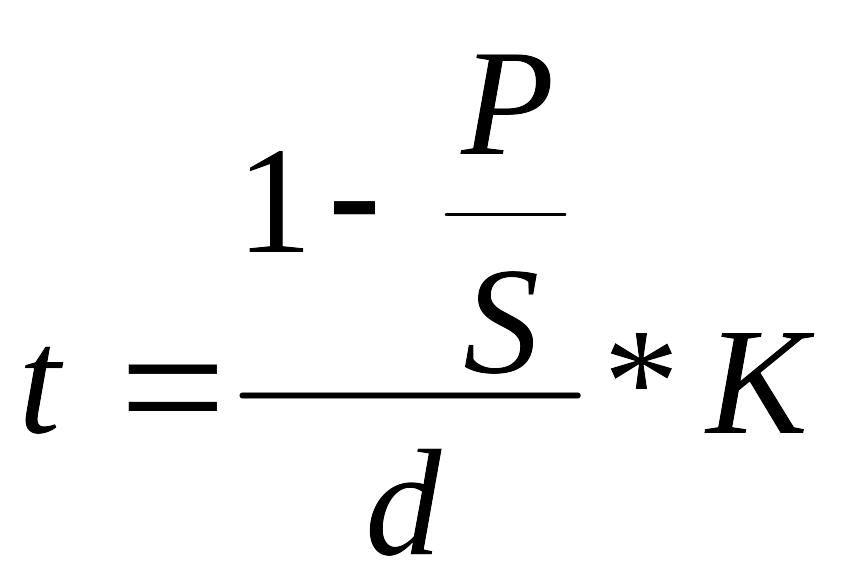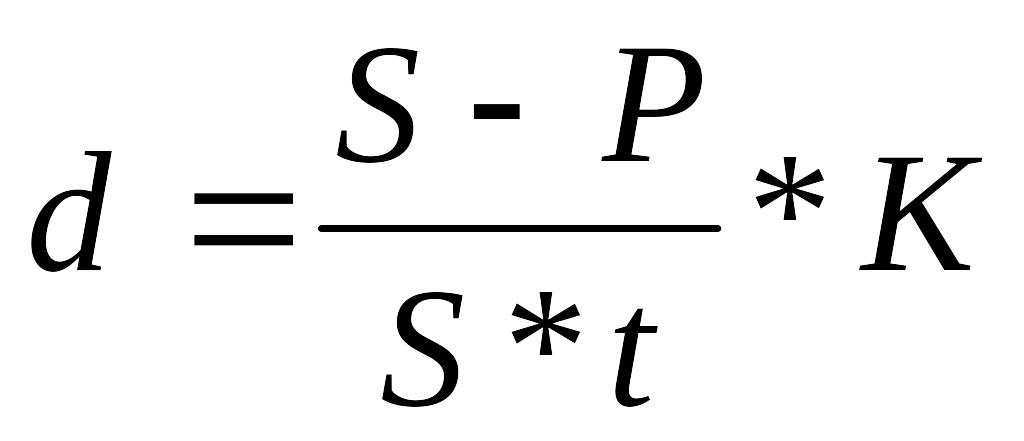2. Прості антисипативні відсотки (t - тривалість у днях, K - тимчасова база)	; (4.23)	; (4.25)

 

Одним з найважливіших параметрів будь-якої фінансової операції являється процентна (облікова) ставка. Вона використовується для оцінки прибутковості. 

Розглянемо способи розрахунку величини процентних (облікових) ставок, коли задані інші параметри фінансової операції. Перетворивши формули декурсивного й антисипативного нарощення простих процентів, отримаємо вираження (4.24) і (4.25) у табл. 4.1.

Без сумніву, дана методика може використовуватися при аналізі будь-яких фінансових операцій, а не тільки в процесі банківського кредитування.

Наприклад, іноземна валюта в обсязі 1000 одиниць, куплена за курсом 10 грн. за 1 одиницю, через місяць була продана за курсом 10 грн. 20 коп. Визначити прибутковість цієї операції по річній простій процентній ставці (комерційні проценти).

Розв’язання.

З формули (4.12) отримаємо:

i = (10200 – 10000) / (10000 * 30) * 360 = 24%.

Аналогічний підхід до розрахунку прибутковості використовується і на фондових ринках.

Так, Національнім банком України була рекомендована формула розрахунку прибутковості ДКО:

 

, (4.26)

де N – номінал облігації;

P – ціна її придбання;

t – термін до погашення.

Прибутковість – це похідна величина, яка не визначає, а яку визначають ті грошові потоки, що породжує кредитна угода (цінний папір чи інший фінансовий інструмент).

Розраховуючи прибутковість фінансової операції, інвестор одержує суб'єктивну оцінку її величини, що залежить від цілого ряду передумов. Наприклад, таких як спосіб нарахування процентів, вибір тимчасової бази і т.п.

Для фінансового менеджменту складні проценти мають незмірно велику цінність, чим прості. Очевидно, що при використанні методики розрахунку простих процентів значення прибутковості неточне вже через те, що дана методика не враховує можливості реінвестування отриманих доходів. Тому при інших рівних умовах безумовно кращим являється розрахунок прибутковості як ставки складних процентів.