1.2 Метод хорд

П усть мы нашли отрезок [a, b], на котором функция f(x) меняет знак. Для определенности примем: f(a )> 0, f(b) < 0 (рисунок 2). В данном методе процесс итераций состоит в том, что в качестве приближений к корню уравнения f(x) = 0 принимаются значения C₀, C₁,... точек пересечения хорды с осью абсцисс.

Сначала находим уравнение хорды:

.

Для точки пересечения ее с осью абсцисс (x = c₀, y = 0) получим уравнение:

.

Далее, сравнивая знаки величин f(a) и f(c₀) для рассматриваемого случая, приходим к выводу, что корень находится в интервале [a, c₀], так как f(a)*f(c₀) < 0. Отрезок [c₀,b] отбрасываем. Следующая итерация состоит в определении нового приближения с₁ как точки пересечения хорды АВ₁ с осью абсцисс и т.д. Итерационный процесс продолжается до тех пор, пока f(c_n) не станет по модулю меньше заданного .

1.3 Метод простой итерации

Для использования этого метода исходное уравнение записывается в виде x = f(x). Пусть известно начальное приближение корня x = c₀. Подставляя это значение в исходное уравнение, получаем новое приближение c₁ = f(c₀). Далее, подставляя каждый раз новое значение корня в уравнение, получим последовательность значений: c_n+1 = f(c_n), n = 1, 2,... Итерационный процесс прекращается, если результаты двух последовательных итераций близки: ¦c_n+1 - c_n¦ < . Достаточным условием сходимости метода простой итерации является условие ¦f '(c_n)¦ < 1.

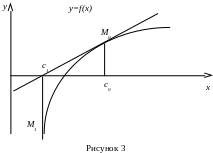
1.4 Метод Ньютона (касательных)

Суть метода состоит в том, что на к-й итерации вместо хорды проводится касательная к кривой y = f(x) при x = c_k и ищется точка пересечения касательной с осью абсцисс. При этом не обязательно задавать отрезок [a, b], содержащий корень уравнения f(x) = 0, а достаточно лишь найти некоторое начальное приближение корня x = c₀ (рисунок 3).

Уравнение касательной, проведенной к кривой y = f(x) в точке М₀ с координатами с₀ и f(c₀), имеет вид:

y - f(c₀) = f'(c₀)(x - c₀).

Отсюда найдем следующее приближение корня с₁ как абсциссу точки пересечения касательной с осью x (y = 0):

c₁ = c₀ - f(c₀)/f'(c₀).

Аналогично могут быть найдены и следующие приближения как точки пересечения с осью абсцисс касательных, проведенных в точках M₁, M₂ и т.д. Формула для n+1-го приближения имеет вид:

c_n+1 = c_n - f(c_n)/f'(c_n). (1)

При этом необходимо, чтобы f'(c_n) не равнялось нулю. Для окончания итерационного процесса может быть использовано или условие ¦f(c_n)¦ < , или условие близости двух последовательных приближений ¦c_n+1 - c_n¦ < .

Из формулы (1) следует, что на каждой итерации объем вычислений в методе Ньютона больший, чем в рассмотренных ранее методах, поскольку приходится находить значение не только функции f(x), но и ее производной. Однако скорость сходимости здесь значительно выше.

Трудность в применении метода Ньютона состоит в выборе начального приближения, которое должно находиться в окрестности D (области нахождения корня). Поэтому иногда целесообразно использовать смешанный алгоритм. Он состоит в том, что сначала применяется всегда сходящийся метод (например, метод деления отрезка пополам), а после некоторого числа итераций - быстро сходящийся метод Ньютона.