1. Метод равномерного распределения точек по отрезку.

Берем какое-то число шагов по отрезку , вычисляем шаг по аргументу , в полученных точках определяем значения функции , из них находим наименьшее. А какое число промежутков надо взять , ведь функция задана лишь в точках ? Критерия выбора количества шагов для достижения заданной погрешности в определении наименьшего значения нет.

Рассмотрим рисунок:

Мы не можем быть уверены в достоверности получаемого результата , так как всегда будет вероятность пропускания действительного минимума из-за «прерывного» характера рассматриваемых значений.

Поэтому при решении вопроса о числе точек и точности важно максимально полно использовать всю дополнительную информацию о свойствах целевой функции. Также важна и интуиция , чувство здравого смысла.

постоянное сравнение результатов .

Многомерные задачи оптимизации.

Подавляющее число задач оптимизации зависят от нескольких параметров.

Характер задачи и методы ее решения зависят от той информации о целевой функции , которая стала доступной в результате исследования. Методы поиска наименьшего значения функции:

Задачи с ограничениями-равенствами. Множители Лагранжа.

В рассмотрение вводится функция

Заметим, что

Теорема:

Пусть функция f дифференцируема в точке , отображение F дифференцируемо в некоторой окрестности этой точки, причем его производная непрерывна в точке .

Тогда если является локальным решением задачи , то найдется такой элемент λ , для которого .

Точка называется стационарной точкой задачи, если . Множитель λ называют множителем Лагранжа, отвечающим точке .

Систему уравнений называют системой Лагранжа.

Пример:

Найти экстремальные точки функции на единичной окружности

Существование точек глобального максимума и минимума вытекает из теоремы Вейерштрасса. Очевидно что для функции F(x)=

1. Метод покоординатного спуска

Пусть надо найти наименьшее значение целевой функции f(x₁,x₂,….,x_n)=f(M)

Точка М – некоторая точка n-пространства.

Выбираем какую-то точку пространства М₀(x₁₀,x₂₀,x₃₀,…,x_n0) и рассматриваем функцию f при всех фиксированных переменных , кроме первой f(x₁,x₂₀,….,x_n0) получаем функцию одной переменной. По первой переменной движемся в сторону убывания функции , пока не достигнем минимума. Переменную в этой точке фиксируем как x₁₁ , точку называем M₁(x₁₁,x₂₀,x₃₀,…,x_n0) Потом аналогично для переменной x₂ находим точку М₂ и так далее.

Для наглядности рассмотрим рисунок. Здесь функция двух переменных u=f(x,y)

Обозначены линии уровня 9,7,5,3,1.

Конечно , надо понимать , что приступая к решению реальной задачи никакого рисунка мы иметь не будем. Данный рисунок только для иллюстрации метода .

2. Метод градиентного спуска.

Рассмотрим определение градиента и антиградиента на примере функции трех переменных.

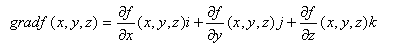
Вектор градиента дает представление о поведении функции в окрестностях точки . Направление вектора градиента есть направление наиболее быстрого возрастания функции в этой точке. Соответственно противоположное направление называют антиградиентом.

Модуль градиента определяет скорость возрастания и убывания функции в направлении градиента и антиградиента. Для всех остальных направлений скорость изменения функции в точке меньше модуля градиента.

Суть метода: двигаться к минимуму в направлении наиболее быстрого убывания функции, которая определяется антиградиентом.

Каким-либо образом выбираем начальную точку, в ней вычисляем градиент функции и делаем шаг в обратном антиградиентном направлении .Нашли точку , в которой значение функции меньше первоначального . Далее процесс повторяется. В данном случае приближение к наименьшему значению будет более быстрым , чем в методе покоординатного спуска.

В случае , если функция задана не аналитически , частные производные вычисляются приближенно с помощью известных конечно-разностных соотношений.

Приращение аргумента не должно быть слишком малым , значения функции должны быть вычислены с высокой степенью точности.

Пример: