8. Исследование движения главного вала машины

После установки маховика определяется угловая скорость кривошипа на стадии установившегося движения для различных положений:

Для удобства анализа результаты вычислений сводятся в таблицу.

№	T0+ΔTi
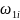
0	56135	6.074
1	56098	6.0746
2	53453	5.929
3	50808	5.7796
4	50771	5.778
5	52047	5.8506
6	53453	5.93
7	54859	6.066

По результатам вычислений строится график зависимости угловой скорости кривошипа от времени. По этому графику определяем угловое ускорение кривошипа в одном расчетном положении. В нашем случае – положение 2.

где - угол между касательной в точке 7 и осью абсцисс. Ускорения центров масс звеньев и их угловые ускорения определяются из плана ускорений, который строится для расчетного (наиболее нагруженного) положения в масштабе µ_a = 0,01м/с²·мм.

Вычисления начинаются с входного звена (кривошипа) несущего механизма. Векторное уравнение ускорения точки А: .

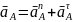Нормальное ускорение точки А:

откладывается в виде вектора πn₁ (параллельно звену ОА).

Касательное ускорение точки А:

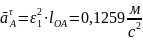
откладывается в виде вектора n₁a (перпендикулярно звену ОА).

Векторное уравнение ускорения точки B – крайней точки шатуна:

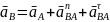
Нормальное ускорение BA:

откладываются в виде векторов an₂ (параллельно звеньям АВ).

Для определения касательного ускорения из точки n₂ (перпендикулярно звену АВ) проводится луч, на пересечении которого с осью OX находится точка b. Модуль ускорения звена B определиться по формуле:

Определим ускорение точки С, принадлежащей 2-му звену. Нормальная составляющая ускорения С₂ определится как:

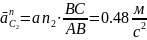
где AB и BC – расстояния, взятые из плана положений механизма.

Направление ускорения совпадает с направлением ускорения .

Из острия вектора проводится отрезок, перпендикулярный звену AB, до пересечения на плане ускорений с линией ab, образуя точку С₂. Величина полного ускорения точки С₂ определится как:

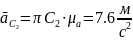
Векторное уравнение ускорения точки С_5, принадлежащей 5 звену:

Кориолисова составляющая ускорения точки C₅ рассчитывается по формуле:

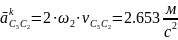
где 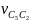- переносная скорость, взятая из плана скоростей.

Кориолисова составляющая откладывается перпендикулярно звену AB, в направлении точки Затем из точки k проводится отрезок, параллельный AB до пересечения с 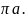Величину ускорения точки C₅ можно определить по формуле:

Ускорения центров масс звеньев и их угловые ускорения:

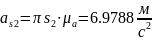
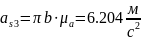
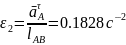
9. Силовой анализ механизма

После нахождения ускорений вычисляются инерционные нагрузки, действующие на звенья:

а) 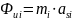– силы инерции.

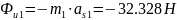
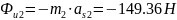
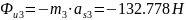
б) – силы инерции.

в) - силы тяжести. g = 9.81 м/с²

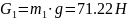
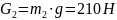
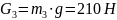
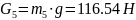
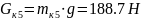
К рабочему органу прикладываем силу полезного сопротивления, которая в соответствии с графиком полезных нагрузок в рассматриваемом положении механизма составляет:

Для определения реакций в кинематических парах, разбиваем передаточный механизм на структурные группы. Отделяем от механизма два последних звена 4 и 5, а действие отброшенных звеньев заменяем реакциями. На звено 5 со стороны стойки 0 действует реакция Р₀₅ , а на звено 4 – реакция со стороны кулисы. Для определения модуля неизвестных реакций строим многоугольник сил:

.

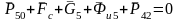где 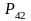- перпендикулярна 4-му звену;

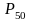- перпендикулярна линии перемещения выходного звена у-у.

Неизвестные реакции и определяются геометрически из плана сил. Для этого в соответствии с уравнением последовательно от точки a откладыва­ются векторы сил 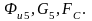Далее через начало (точку а) и через окончание плана сил (точку d) проводятся лучи перпенди­кулярно соответственно 4-му звену и ли­нии у-у, на пересечении которых находится точка, определяющая величины векторов и .

Величины векторов и равны:

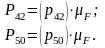
Учитывая, что масштаб построения неизвестные реакции оказались равны:

Для структурной группы 2-3 векторное уравнение сил:

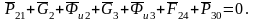
находим , составив уравнение моментов относительно точки А:

,

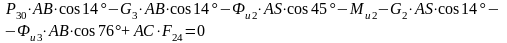Аналогично образом находим , составив уравнение моментов относительно точки А.

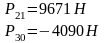
Неизвестную х-овую составляющую реакции 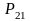определим геометрически из плана сил, для чего последовательно откладываются векторы сил и проводятся лучи параллельно соответственно звеньям АВ и ВС.

Для начального звена (кривошипа OA) векторное уравнение сил:

где - сила тяжести колеса уравнительной пары; - сила тяжести кулачка; 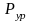- сила, действующая в зацеплении уравнительной пары (под углом 20° к касательной к основной окружности). Уравновешивающая сила определяется из уравнения моментов сил относительно точки О:

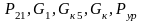Неизвестная реакция определяется из плана сил, для чего последовательно откладываются векторы сил и проводится вектор, замыкающий силовой многоугольник.

_{Величина реакции} равна: