Тема IV. Производная и её применение Определение производной. Правила дифференцирования. Таблица производных

Пусть функция определена на промежутке X. Выберем точку и зададим приращение аргумента (независимой переменной) . Тогда приращение функции составит .

Определение 4.1. Производной функции в точке называется предел отношения приращения функции к приращению аргумента, когда последний стремится к нулю (при условии, что указанный предел существует). Обозначается

.

Определение 4.2. Если функция имеет в точке конечную производную, то она называется дифференцируемой в данной точке. Функция, дифференцируемая в каждой точке промежутка Х, называется дифференцируемой на данном промежутке. Операция нахождения производной называется дифференцированием.

Продифференцируем некоторые функции, пользуясь определением производной.

Пример 4.1. Пусть - некоторая постоянная (константа), тогда , то есть .

Пример 4.2. Пусть , тогда

= , то есть дифференцируема на и .

!Самостоятельно найти производные для функций !

Пример 4.3. Пусть , тогда = =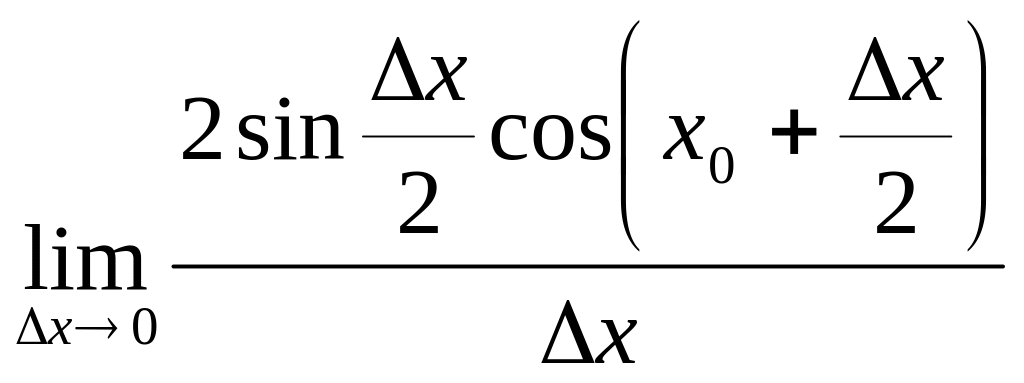 = 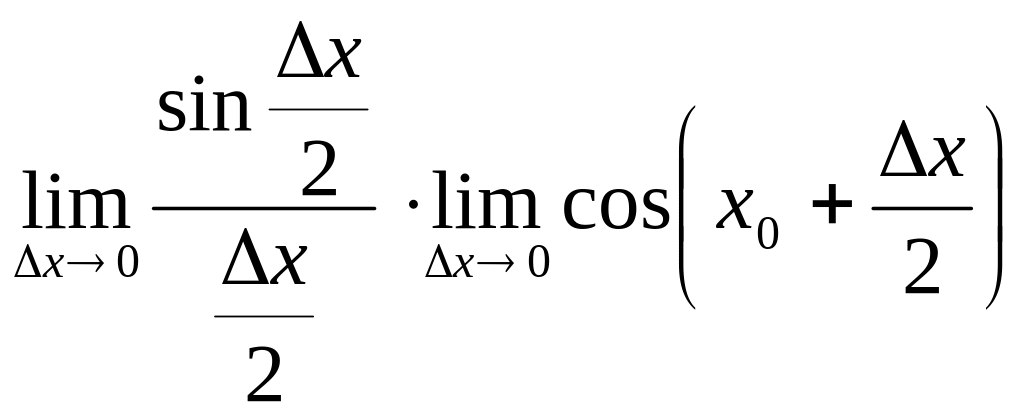(первый предел имеет место как «замечательный», второй – в силу непрерывности функции ). Таким образом, дифференцируемая на и .

!Самостоятельно найти производную для функции !

Пример 4.4. Пусть , тогда =

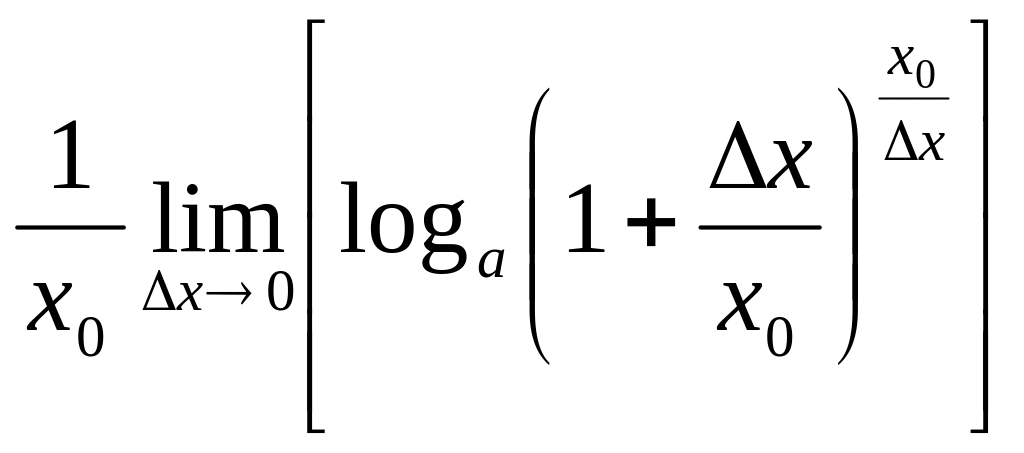= = = = в силу непрерывности логарифма = = в силу второго «замечательного» предела = , или, в более удобной записи, .

Следствие. - доказать самостоятельно.

Теорема 4.1 (необходимое условие дифференцируемости). Если функция дифференцируема в точке , то она является непрерывной в данной точке. Так, например, функция не является дифференцируемой в точках , поскольку она является разрывной в этих точках.

Замечание. Обратное утверждение неверно. Так, например, функция непрерывна в точке , однако не является дифференцируемой в данной точке. Покажем это

предел слева не равен пределу справа, следовательно, у функции не существует производной в точке .

Теорема 4.2 (арифметические свойства производной). Пусть функции и дифференцируемы в точке . Тогда функции , и также дифференцируемы в точке и их производные вычисляются по формулам

, (1)

, (2)

. (3)

Доказательство. (1) =

= ;

(2) = =

= =

= = .

Заметим, что предельное соотношение имеет место в силу дифференцируемости, а значит и непрерывности, функции в точке .

Следствие. Постоянный множитель можно выносить за знак интеграла (доказать самостоятельно).

Пример 4.5. Пусть , тогда получим

.

!Самостоятельно найти производную для функции !

Теорема 4.3 (производная сложной функции). Если функция дифференцируема в точке , а функция дифференцируема в соответствующей точке , то сложная функция дифференцируема в точке и .

Другими словами, производная сложной функции равна произведению производной внешней функции соответствующего аргумента на производную внутренней функции. Привести пример функций и .

Пример 4.6. Пусть , тогда или . Продифференцировав обе части, получим или , то есть на области определения.

Теорема 4.4 (производная обратной функции). Если функция имеет в точке отличную от нуля производную , то обратная функция также имеет производную в точке , вычисляемую по формуле .

Пример 4.7. Поскольку функция является обратной к функции , то , .

Замечание. Аналогично выводятся формулы для остальных обратных тригонометрических функций.

Пример 4.8. Поскольку функция является обратной к функции , то .

Следствие. .

Таблица производных

Пример 4.9. Пользуясь таблицей производных, правилами дифференцирования и теоремой о производной сложной функции, найти производную следующей функции

.