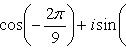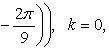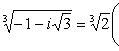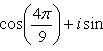- •Комплексные числа
- •1. Понятие мнимой единицы
- •2. Степени мнимой единицы
- •3. Определение комплексного числа
- •4. Действия над комплексными числами в алгебраической форме
- •5. Геометрическая интерпретация комплексного числа
- •6. Тригонометрическая форма комплексного числа
- •7. Показательная форма комплексного числа
7. Показательная форма комплексного числа
Если комплексному числу z = (cos j + i sin j), модуль которого равен 1, поставить в соответствие показательное выражение eij, то получим соотношение
cos j + i sin j = eij, (4)
которое называется формулой Эйлера.
Любое комплексное число z можно записать в виде z = reij.
Эта форма записи комплексного числа называется показательной формой.
Итак, существуют три формы записи комплексного числа:
z = a + bi – алгебраическая форма; z = r (cos j + i sin j) – тригонометрическая форма; z = reij – показательная форма.
Пример 12. Записать число
в показательной форме.
Решение.
Здесь
![]()
Следовательно, показательная форма числа имеет вид
![]()
Возвышение в степень комплексных чисел
Применяя формулу умножения комплексных чисел в случае n равных сомножителей, получаем правило возвышения комплексного числа в целую положительную степень:
[r (cosj + i sinj)]n = r n(cos n j + i sin n j), |
(11) |
т.е. для возвышения комплексного числа в целую положительную степень нужно его модуль возвысить в эту степень и аргумент умножить на показатель степени. Полагая в формуле (11) r = 1, получаем формулу Моавра:
(cosj + i sinj)n = (cos n j + i sin n j) |
Извлечение корня из комплексного числа
Корнем n-й степени из комплексного числа называется такое комплексное число, n-я степень которого равна подкоренному числу. Таким образом, равенство:
![]()
равносильно равенству
rn(cos ny + i sin ny) = r (cos j + i sin j)
Но у равных комплексных чисел модули должны быть равны, и аргументы могут отличаться лишь кратным 2p, т.е.
rn = r, ny = j + 2kp,
откуда
![]()
где
![]() есть
арифметическое значение корня и k
- любое целое число. Таким образом мы
получаем:
есть
арифметическое значение корня и k
- любое целое число. Таким образом мы
получаем:
|
(16) |
т.е. для извлечения корня из комплексного числа надо извлечь корень из его модуля, а аргумент разделить на показатель корня. В формуле (16) число k может принимать всевозможные целые значения; однако можно показать, что различных значений корня будет только n, и они будут соответствовать значениям:
k = 0, 1, 2, ..., (n-1) |
(17) |
Чтобы
доказать это, заметим, что правые части
в формуле (16) будут различными при двух
различных значениях k
= k1
и k
= k2
тогда, когда аргументы
![]() и
и
![]() отличаются
не кратным 2p, и будут одинаковыми, если
указанные аргументы отличаются кратным
2p.
Но разность (k1
- k2)
двух чисел из ряда (17) по абсолютному
значению меньше n,
а потому разность
отличаются
не кратным 2p, и будут одинаковыми, если
указанные аргументы отличаются кратным
2p.
Но разность (k1
- k2)
двух чисел из ряда (17) по абсолютному
значению меньше n,
а потому разность
![]()
не может быть кратна 2p, т.е. n значениям k из ряда (17) соответствуют n различных значений корня. Пусть теперь k2 - целое число (положительное или отрицательное), не заключающееся в ряде (17). Мы можем представить его в виде:
k2 = qn + k1
где q - целое число и k1 - любое число из ряда (17), а потому
![]() ,
,
т.е. значению k2 соответствует то же значение корня, что и значению k1, заключающемуся в ряде (17). Итак, корень n-й степени из комплексного числа имеет n различных значений. Исключение из этого правила представляет лишь частный случай, когда подкоренное число равно нулю, т.е. r = 0. В этом случае все указанные выше значения корня равны нулю.
Найти
все значения корней: а)
![]() ; б)
; б)
![]() .
.
Решение.
а) Запишем комплексное число 1 в тригонометрической форме 1 = cos 0° + i sin 0°; затем по формуле (1), находим
![]()
![]()
![]()
Следовательно,
![]()
![]() при k
= 0;
при k
= 0;
![]()
![]() при k
= 1;
при k
= 1;
![]()
![]() при k
= 2;
при k
= 2;
![]()
![]() при k
= 3.
при k
= 3.
б)
Записав комплексное число
![]() в
тригонометрической форме
в
тригонометрической форме
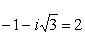
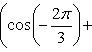
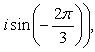
находим
![]()
![]()
![]()
![]()
Отсюда