
Лекции по кинематике и динамике поступательного движения
.doc
Лекция 1: Кинематика поступательного и вращательного движения
План:
-
Модуль и направление углового перемещения.
-
Модуль и направление угловой скорости.
-
Мгновенная угловая скорость.
-
Связь линейной и угловой скоростей.
-
Модуль и направление углового ускорения.
-
Связь тангенциального и углового ускорения.
-
Мгновенное угловое ускорение.
-
Модуль и направление углового перемещения
Движение тела по криволинейной траектории можно приближенно представить как движение по дугам некоторых окружностей см. рис.1.
Пусть произвольная точка М сначала
находилась в неподвижной плоскости Q
(рис. 2). Затем переместилась в подвижной
плоскости P на угол
поворота
![]() .
.
Угол поворота (угловое перемещение) будим отсчитывать от неподвижной плоскости Q по часовой стрелке (см. рис. 3).
![]()
![]()
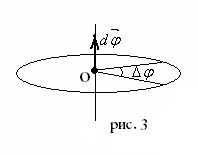
Направление углового
перемещения
![]() совпадает с направлением поступательного
движения острия винта, головка которого
вращается в направлении движения точки
по окружности, т.е. подчиняется правилу
правого винта.
совпадает с направлением поступательного
движения острия винта, головка которого
вращается в направлении движения точки
по окружности, т.е. подчиняется правилу
правого винта.
Модуль углового перемещения запишется по аналогии с координатой:
|
|
|
|
-
Модуль и направление угловой скорости
При малом угловом перемещении
![]() равен (1)
равен (1)
![]() (2)
(2)
Разделим обе части последнего выражения
на
![]() :
:
![]() или (3)
или (3)
![]() (4)
(4)
где выражение
![]() - есть средняя угловая скорость, т.е
- есть средняя угловая скорость, т.е
![]() ,
(5)
,
(5)
![]()
![]()
Вектор угловой
скорости
направлен вдоль
оси вращения по правилу
правого винта,
т.е. также как и вектор
![]()

Модуль угловой скорости запишется по аналогии с линейной скоростью:
|
|
|
|
5. Мгновенная угловая скорость.
Мгновенная угловая скорость равна первой производной углового перемещения по времени:
![]() (6)
(6)
При равномерном вращении
![]() ,
тогда
,
тогда
![]() (7)
(7)
6. Связь линейной и угловой скоростей.
Если продолжить (3), то получим:
![]() или
или
![]() (8)
(8)
![]() (9)
(9)

Вектор линейной
скорости
совпадает по
направлению
с векторным произведением
![]() .
Векторное произведение всегда связано
с правилом
правого винта:
вращая головку винта по направлению
вектора
.
Векторное произведение всегда связано
с правилом
правого винта:
вращая головку винта по направлению
вектора
![]() ,
стоящего на первом месте в (9), к вектору
,
стоящего на первом месте в (9), к вектору
![]() ,
стоящему на втором месте, определяем
по поступательному движению винта
направление третьего вектора
,
стоящему на втором месте, определяем
по поступательному движению винта
направление третьего вектора
![]() ,
см. рис. 5.
,
см. рис. 5.
Модуль векторного произведения:
![]() (10)
(10)
7. Модуль и направление углового ускорения.
При
вращении за время
![]() угловая скорость получит приращение
угловая скорость получит приращение
![]() ,
тогда (8) примет вид:
,
тогда (8) примет вид:
![]()
![]()
![]() (11)
(11)
Разделим обе части
на
![]() ,
получим:
,
получим:
![]() ,
(12)
,
(12)
где отношение
![]() - есть среднее угловое ускорение.
- есть среднее угловое ускорение.
 т.е.
т.е.
![]() (13)
(13)
Вектор
углового ускорения
![]() сонаправлен с вектором угловой скости
при
сонаправлен с вектором угловой скости
при
![]() и противоположен ему при
и противоположен ему при
![]() ,
см. рис 6.
,
см. рис 6.
8. Связь тангенциального и углового ускорения.
При вращении за
время
![]() угловая скорость получит приращение
угловая скорость получит приращение
![]() ,
тогда (8) примет вид:
,
тогда (8) примет вид:
![]()
![]()
![]() (14)
(14)
Разделим обе части
на
![]() ,
получим:
,
получим:
![]() (15)
(15)
или
![]() (16)
(16)
Векторное произведение:
![]() (17)
(17)
Вектор тангенциального
ускорения
совпадает по направлению с векторным
произведением
![]() .
Векторное произведение всегда связано
с правилом
правого винта:
вращая головку винта по направлению
вектора
.
Векторное произведение всегда связано
с правилом
правого винта:
вращая головку винта по направлению
вектора
![]() ,
стоящего на первом месте в (13), к вектору
,
стоящего на первом месте в (13), к вектору
![]() ,
стоящему на втором месте, определяем
по поступательному движению винта
направление третьего вектора
,
стоящему на втором месте, определяем
по поступательному движению винта
направление третьего вектора
![]() .
.
9. Мгновенное угловое ускорение.
При
![]() получим мгновенное угловое ускорение:
получим мгновенное угловое ускорение:
![]() ,
(18)
,
(18)
т.е. мгновенное угловое ускорение численно равно первой производной угловой скорости по времени или – второй производной углового перемещения по времени.
Приложение 1.
|
тип движения
|
рисунок, графики |
формулы |
|
|
Равномерное движение |
|
|
|
|
Равноускоренное (равнозамедленное) движение |
|
|
|
|
|
|
||
|
Движение тела, брошенного вертикально вниз |
|
При
|
|
|
При
|
|||
|
Движение тела, брошенного вертикально вверх |
|
|
|
|
При
|
|||
|
Движение тела, брошенного горизонтально |
|
|
|
|
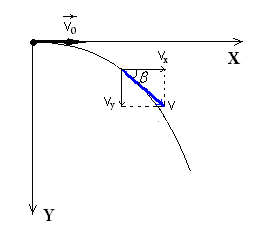
Движение тела, брошенного под углом к горизонту |
|
|
|
|
Движение тела по окружности |
Т
При движении по криволинейной траектории
изменяется не только модуль скорости,
но и ее направление, поэтому вектор
ускорения представляют в виде двух
составляющих: тангенциального (
Тангенциальное (касательное) ускорение – составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке. (Тангенциальное ускорение характеризует изменение скорости по модулю;
Направление вектора
Нормальное ускорение – составляющая
вектора ускорения, направленная вдоль
нормали к траектории в данной точке.
(Нормальное ускорение характеризует
изменение скорости по направлению.
Вектор
Модуль полного ускорения при этом определяется соотношением:
Направление полного ускорения определяют правилом сложения векторов:
|
|
|









 ангенциальное
и нормальное ускорение.
ангенциальное
и нормальное ускорение.