Решение.

Силу сопротивления воздуха не учитываем, следовательно,

систему «пуля-шар» можно считать замкнутой. Запишем закон

сохранения импульса и энергии для данной системы:

mv = (m+M)u (1) , Рис.2.

где u-скорость шара вместе с пулей после удара.. В результате взаимодействия шара с пулей, он приобрел кинетическую энергию, которая после отклонения стержня на < перешла в потен -циальную энергию

(2).

Из (1) выразим u:

u = или u = = .

Из (2) получим :

.

Найдем h.

ВМ= , h= ; , тогда

.

Проверим единицы измерения v.

.

Проведем вычисления v. 550(м/с).

Ответ:v =550м/с.

Задача 4. Найти работу А , которую надо совершить, чтобы сжать пружину на =20 см, если известно, что сила F пропорциональна сжатию и жесткость пружины k = 2,94 кН/м.

Дано: =20 см =0,2м, k = 2,94 кН/м=2,94.10 ³ Н/м.

Определить А.

Решение

Работа, совершаемая при сжатии пружины, определяется формулой

(1),

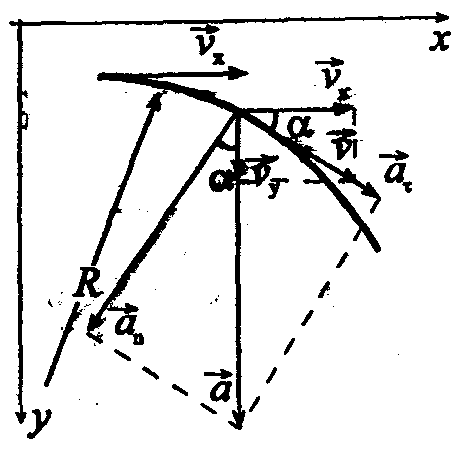г де — сжатие. По условию сила пропорциональна сжатию, т.е. F = - k — (2). Подставляя (2) в (1), получим

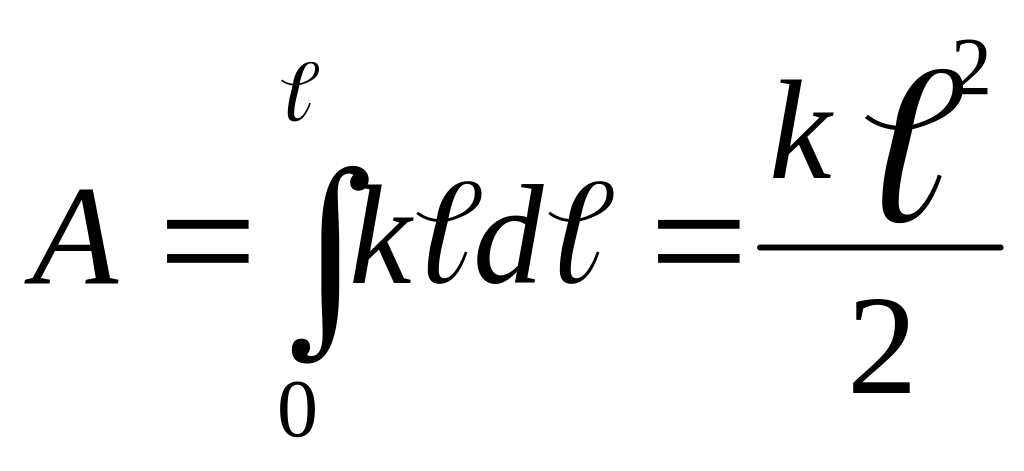.А = 58,8 Дж.

Проверим единицы измерения А.

Проведем вычисления А. Рис.3

Ответ: А=58,8Дж.

Задача 5. Камень брошен горизонтально со скоростью v _{x =} 10 м/с . Найти радиус кривизны R траектории камня через время t=3с после начала движения.

Дано: v _x=10м/с, t=3с.

Определить R.

Решение.

Нормальное ускорение камня

(1);

из рисунка видно, что

(2).

Из уравнения (1)

, где .

Кроме того ; .Сделав соответствующие подстановки,

получим .

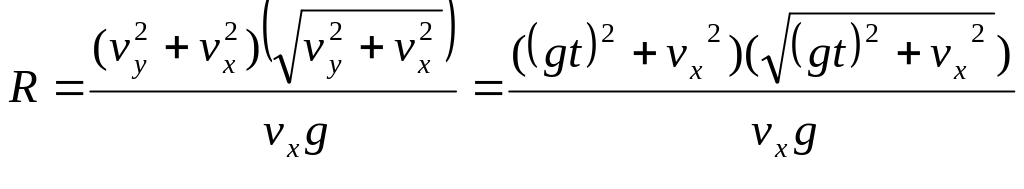Проверим единицы измерения и проведем вычисления искомой величины.

, R=

Ответ R=305м.

Задача 6. Два свинцовых шара массами m ₁= 2 кг и m ₂ = 3 кг подвешены иа нитях длиной = 70 см. Первоначально шары соприкасаются между собой, затем меньший шар откло-нили на угол = 60 ⁰ и отпустили (рис. 4). Считая удар центральным и неупругим, опре-делить: 1) высоту h, на которую поднимутся шары после удара; 2) энергию , израсходованную на деформацию шаров при ударе.

Дано:m ₁=2кг,m ₂=3кг, =7Осм =0,7м, =60 ⁰.

Определить: 1) h ; 2) .

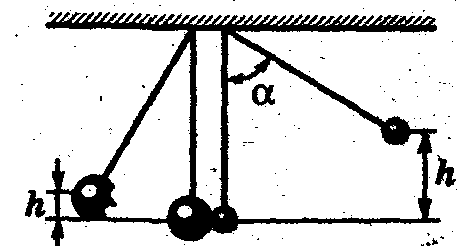Решение. Удар неупругий, поэтому после удара шары движутся с Рис.4

общей скоростью v, которую найдем из закона сохранения импульса: , (1)

где v₁ и v₂ — скорости шаров до удара. Скорость v₁ малого шара найдем Рис.4

из закона сохранения механической энергии:

,

откуда

(2)

(учли, что h ₁ = (1—соs )).

Из выражений (1) и (2) при условии , что v ₂= 0, получим

. (3) Из закона сохранения механической энергии имеем

,

Откуда искомая высота

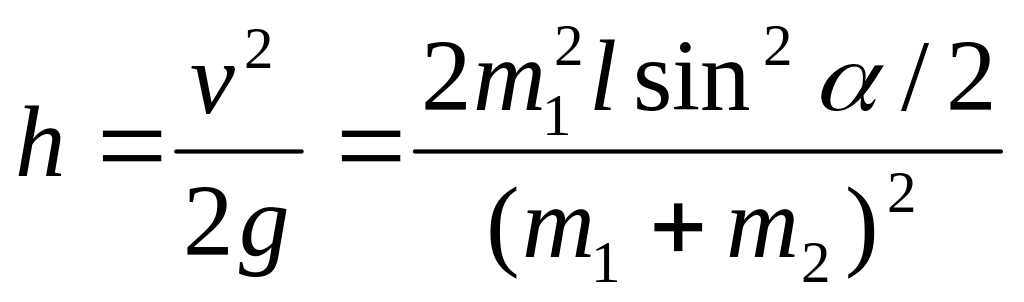
(учли формулу (3)).

Энергия израсходованная на деформацию шаров при ударе,

,

или подставив (2) в (4), находим

.

Проверим единицы измерения определяемых величин и проведем вычисления.

, .

,

Ответ: 1) h=5,6 cм ; 2) Т= 4,12 Дж.

З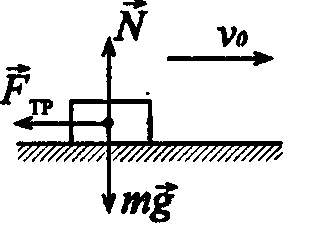 адача 7. Камень, пущенный по поверхности льда со скоростью v =3 м/с, прошел до остановки расстояние s. = 20,4 м. Найти коэффициент трения k камня о лед.

Дано: v=3 м/с, s=20,4м.

Определить k.

Решение. Рис.5

Работа силы трения при скольжении камня по льду равна

А = F_тр S cos ,

где F _тр =k mg cos , cos180 ⁰=-1, тогда А = -k mgS - (1). С другой стороны, работа силы трения равна приращению кинетической энергии камня А =W ₂ -W _1.

Поскольку W ₂ =0, то А = - W ₁ = - — (2). Приравнивая правые части уравнений (1) и (2), получим . Единиц измерения k не имеет.

Подставив числовые значения и вычисляя получим:

k=

Ответ k=0,02.

З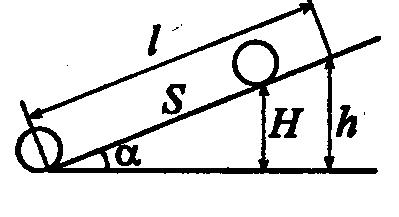 адача 8. Мальчик катит обруч по горизонтальной дороге со скоростьюv = 7,2 км/ч. На какое расстояние s может вкатиться обруч на горку за счет его кинетической энергии? Уклон горки равен IО м на каждые IОО м пути.

Дано: v=7,2 км/ч=2 м/с, h=10 м , =100 м.

Определить S. Рис.6

Решение.

У основания горки обруч обладал кинетической энергией W _k , которая складывалась из кинети-ческой энергии поступательного движения и кинетической энергии вращения. Когда обруч вка-тился на горку на расстояние s , его кинетическая энергия перешла в потенциальную.

W _k. =W_п

Момент инерции обруча J= mR² , частота вращения . Тогда

Следовательно, mv ² = mgН, откуда

Из (рис.6) видно, что , откуда

или .

П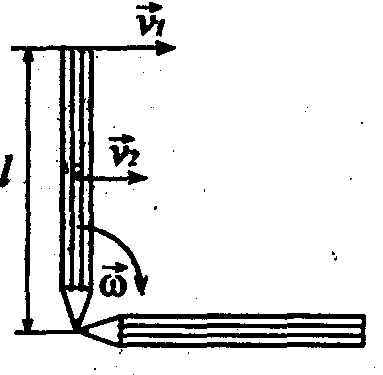 роверим единицы измерения S.

Подставив числовые данные, получим:

S = Рис.7.

Ответ S=4,1м.

Задача 9. Карандаш длиной 1=15 см, поставленный вертикально, падает на стол. Какую угловую скорость и линейную скорость v будет иметь в конце падения середина и верхний конец карандаша?

Дано: см =0,15м.

Определить: v₁ и v _2.