3. Линейные операторы и функционалы в пространстве финитных функций.

Сформулируем необходимое и достаточное условие непрерывности линейного функционала на пространстве .

Теорема 1 (критерий непрерывности линейного функционала на пространстве ).

Линейный функционал на пространстве непрерывен тогда и только тогда, когда он непрерывен на любом подпространстве .

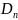Доказательство. Пусть f— линейный функционал на пространстве . В силу определения функционал f непрерывен тогда и только тогда, когда .

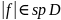Тогда, используя определение полинормы в пространстве , преднорма тогда и только тогда, когда сужение преднормы на любом подпространстве принадлежит .

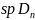Но сужение преднормы 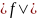на подпространство совпадает с модулем функционала, который является сужением функционала f на подпространстве .

Таким образом, преднорма тогда и только тогда, когда

сужение функционала f на любое подпространство непрерыв­но, т.е. функционал f непрерывен тогда и только тогда, когда его сужение на любое подпространство непрерывно, что и требовалось доказать.

Теорема 2 (критерий непрерывности линейного оператора, определенного на пространстве ).

Линейный оператор, отображающий в полинормированное пространство, непрерывен тогда и только тогда, когда он непрерывен на любом подпространстве .

В качестве примера применения теоремы 2 рассмот­рим оператор дифференцирования , определенный на всем пространстве следующим образом: .

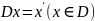Очевидно, что — линейный оператор, отображающий про­странство в пространство . Докажем его непрерывность. Зафиксируем 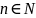и рассмотрим сужение оператора на подпространстве .

Тогда для любого 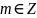и любого 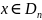имеем: ,

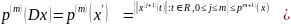: t Е IR, О < j run} ~ p (m+') (x),

откуда следует, что — непрерывный оператор, действующий в . Следовательно, применяя теорему, получим, что оператор является непрерывным оператором из в .

Теорема 3 (секвенциальный критерий непрерывности линейного функционала на пространстве ).

Линейный функционал f на пространстве непрерывен тогда и только тогда, когда для любой последовательности 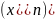, сходя­щейся к нулю в пространстве , числовая последовательность 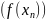сходится к нулю.

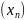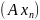Теорема 4 (секвенциальный критерий непрерывности линейного оператора, определенного на ),Пусть Y - полинормированное пространство.Линейный оператор непрерывен тогда и только тогда, когда для любой последовательности из , сходящейся к нулю в пространстве , последовательность сходится к нулю в пространстве .

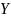Теорема 5 (o непрерывности ограниченного линейного оператора на пространстве ).Пусть полинормированное пространство.

Линейный оператор непрерывен тогда и только тогда, когда онограничен.

Следствие (o непрерывности ограниченного функционала на пространстве ).

Линейный функционал на пространстве непрерывен тогда и ТОЛЬКО тогда, когда он ограничен.

Непрерывные линейные функционалы на пространстве в тео­рии обобщенных функций называются обобщенными функциями.

Теорема 6 (об эквивалентных условиях непрерывности линей­ного функционала на пространстве ).

Пусть 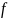–линейный функционал на пространстве .

Следующие условия эквивалентны:

1. f непрерывен;

2. f непрерывен на любом подпространстве ;

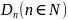3. для любой последовательности , сходящейся к нулю в пространстве , числовая последовательность сходится к нулю;

4. f ограничен.