Резонанс токов в пассивных двухполюсниках.

Резонанс токов наблюдается в электрической цепи с параллельно соединенными участками, обладающими индуктивностью и емкостью и образующими параллельный колебательный контур, который получает энергию от источников синусоидального напряжения, последовательно соединенного с контуром.

Рассмотрим явление резонанса токов в цепи, изображенной на рисунке 1. Пусть первая ветвь содержит активное R₁ и индуктивное ωL сопротивление, а вторая ветвь – емкостное .

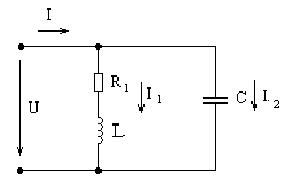
Рисунок 1

Если к цепи, изображенной на рисунке 1, приложено синусоидальное напряжение

, (1)

то ток в неразветвленной части цепи равен

(2)

где G – активная проводимость цепи

(3)

B – реактивная проводимость цепи

(4)

(5)

(6)

φ – сдвиг фаз между током и напряжением на входе цепи

(7)

Из (7) видно, что ток на входе цепи может:

1. отставать от приложенного напряжения на угол φ, если , φ>0;

2. опережать приложенное напряжение, если , φ<0;

3. совпадать по фазе с приложенным напряжением, если , φ=0.

Резонанс токов в параллельном колебательном контуре возникает в момент, когда реактивные проводимости ветвей будут равны между собой и полностью компенсируют друг друга:

или (8)

При этом противоположные по фазе реактивные составляющие токов равны (рисунок 2а), поэтому резонанс в рассматриваемой цепи получил название резонанса токов. Из векторной диаграммы видно, что при резонансе ток I на входных выводах контура может быть значительно меньше токов в ветвях.

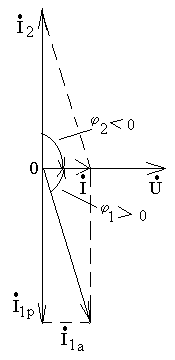
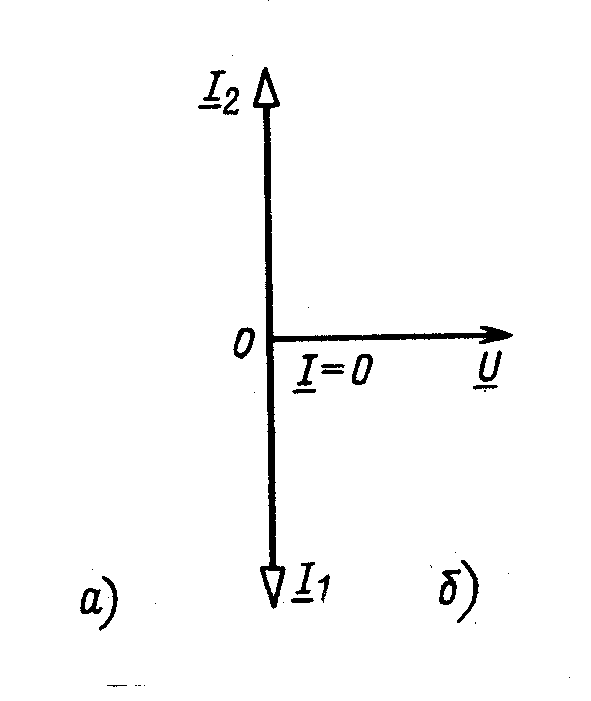
Рисунок 2

Условие резонанса токов можно записать следующим образом:

(9)

При резонансе токов полная проводимость цепи достигает минимального значения и ток на входе цепи тоже достигает своего минимального значения и будет равен своей активной составляющей .

В теоретическом случае, если цепь не имеет потерь , что практически невозможно, токи I₁ и I₂ сдвинуты по фазе относительно напряжения на углы +π∕2 и -π∕2 (рисунок 2б) и суммарный ток I равен 0. Входное сопротивление цепи в данном случае достаточно велико, что приведет к значительному увеличению напряжения в цепи.

Резонанса токов можно достигнуть изменением , C, L или R₁, но не всегда можно достигнуть резонанса изменением того или иного параметра, поэтому для достижения резонанса токов необходимо выполнение следующего условия: .

Значение угловой резонансной частоты может быть получено из условия В=0.

Резонансный контур характеризуется следующими параметрами:

- характеристическим сопротивлением

- добротностью контура

Зависимости реактивных проводимостей и полной проводимости реального колебательного контура от частоты приложенного напряжения источника изображены на рисунке 3а. Емкостная проводимость В₂=В_С с увеличением частоты  возрастает прямо пропорционально частоте, индуктивная проводимость В₁=В_L уменьшается обратно пропорционально частоте. При резонансе проводимости равны, а полная проводимость равна (1/R₁).

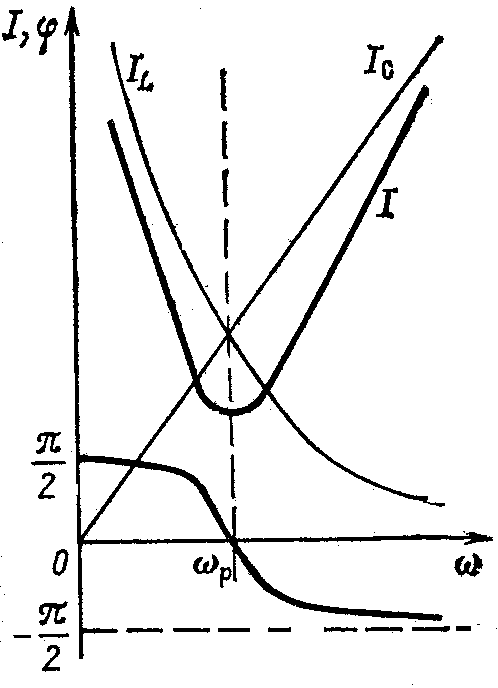
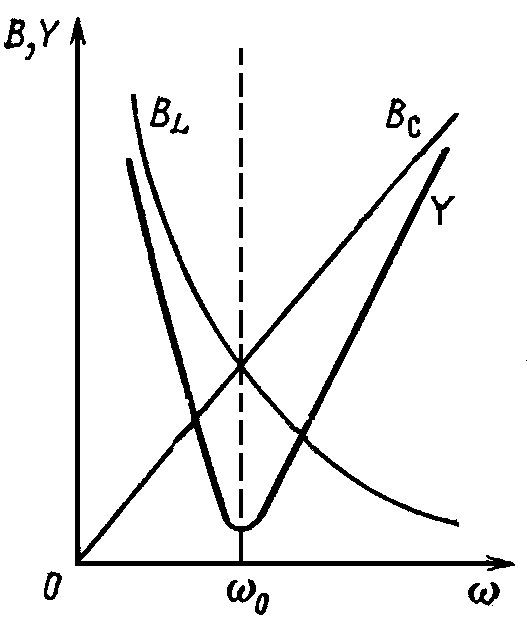
а) б)

Рисунок 3

Резонансные кривые токов, изображенные на рисунке 3б, подобны графикам соответствующих проводимостей. При изменении частоты  от 0 до <_P сдвиг фаз между напряжением и общим током положителен и равен , при _Р сдвиг фаз равен нулю (резонанс), при _Р сдвиг фаз отрицателен и равен  (рисунок 3б).

Имея резонансную кривую и проведя прямую , можно определить затухание цепи как длину отрезка этой прямой, заключенного между точками пересечения ее с резонансной кривой. Следовательно, чем меньше затухание, тем острее резонансная кривая и тем резче выражен резонанс. Отрезок прямой, характеризующий затухание, определяет полосу пропускания контура.