Приложение в Резонанс напряжений в пассивных двухполюсниках.

Резонансом электрической цепи называется такое состояние цепи, когда, несмотря на наличие реактивных элементов в цепи ток и напряжение на входе цепи совпадают по фазе.

Рассмотрим цепь (рисунок 2), состоящую из последовательно соединенных активного сопротивления, катушки индуктивности и конденсатора и подключенную к источнику синусоидального напряжения

(1)

Рисунок 2

Полное сопротивление данной цепи можно определить по формуле:

, (2)

где R – суммарное активное сопротивление цепи (необходимо учитывать активное сопротивление катушки индуктивности),

, (3)

где R_Н – активное сопротивление нагрузки,

R_К – активное сопротивление катушки индуктивности,

X - реактивное сопротивление цепи

(4)

Тогда действующее значение тока в цепи

(5)

Угол сдвига фаз между входным напряжением и током, протекающим по цепи

(6)

Из этой формулы видно, что угол сдвига фаз может быть положительным и отрицательным, в зависимости оттого какое сопротивление в цепи преобладает: если индуктивное ( ), то >0, а если емкостное ( ), то <0; условием резонанса в рассматриваемом контуре будет равенство нулю реактивного сопротивления, т.е. Х=0 или . Изменение частоты приводит к изменению реактивного сопротивления цепи, а изменение реактивного сопротивления ведет к изменению режима цепи. Зависимости параметров цепи от частоты называют частотными характеристиками. Частотные характеристики для рассматриваемой схемы изображены на рисунке 3.

Рисунок 3

При соблюдении данного равенства ток в контуре становится максимальным

(7)

и совпадающим по фазе с входным напряжением.

К условию резонанса в данном контуре можно прийти изменением частоты или параметров динамических элементов (L,C).

; ; (8)

Резонансу в рассматриваемом контуре соответствует векторная диаграмма, изображенная на рисунке 4.

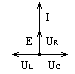
Рисунок 4

Из диаграммы видно, что при резонансе приложенное на­пряжение равно падению напряжения на активном сопротивле­нии цепи:

U=U_R (9)

Напряжения на емкости U_C и индуктивности U_L рав­ны по величине и противоположны по фазе и поэтому взаимно уравновешиваются. При резонансе в рассматриваемом контуре напряжения на емкости и на индуктивности могут оказаться значительно больше приложенного напряжения. Поэтому резонанс при последова­тельном соединении называется резонансом напряжений.

Указанные местные перенапряжения возможны при опреде­ленном соотношении между параметрами контура, а именно при условии .

В частотной области цепь характеризуется следующими величинами:

- характеристическим (волновым) сопро­тивлением контура;

- доброт­ностью контура;

- коэффици­ентом затухания контура.

Перенапряжения в контуре будут иметь место, если добротность контура Q больше единицы.

Для рассматриваемого контура можно построить резонансную кривую тока - зависимость тока от частоты на основании формулы (3). Аналогичные кривые можно построить и для напряжений на динамических элементах (L,C).

(10)

(11)

На рисунке 5 показаны резонансные кривые , f() для Q 1,25.

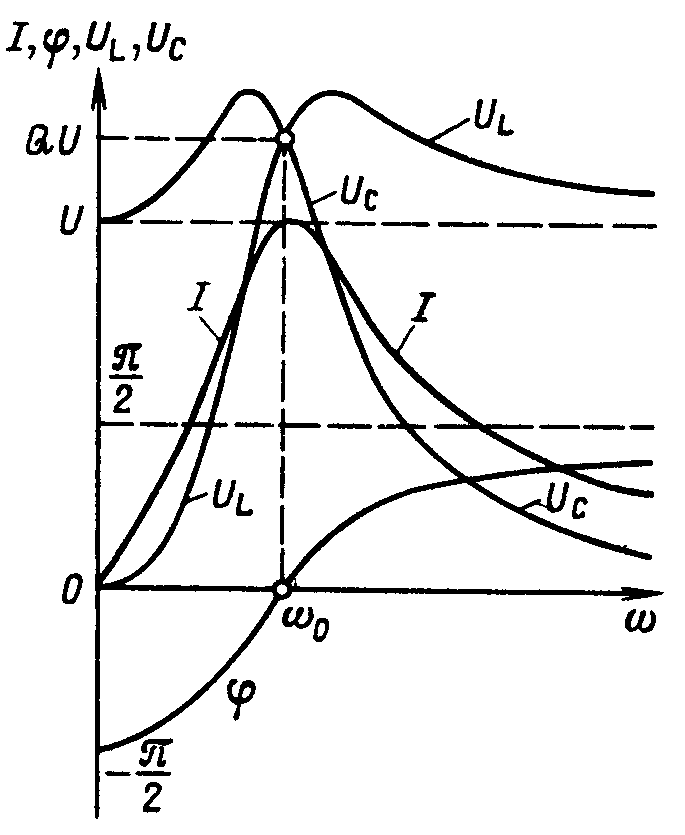
Рисунок 5

Резонансная кривая тока достигает максимума при резонансной частоте . Резонансная кривая достигает максимума при более высокой частоте , а резонансная кривая достигает максимума при более низкой частоте . Максимальные значения этих напряжений одинаковы .

На рисунке 5 изображена также и фазо-частотная характеристика, из которой видно, что угол сдвига фаз между напряжением и током изменяется в пределах {-90;+90} и достигает нулевого значения при резонансной частоте.

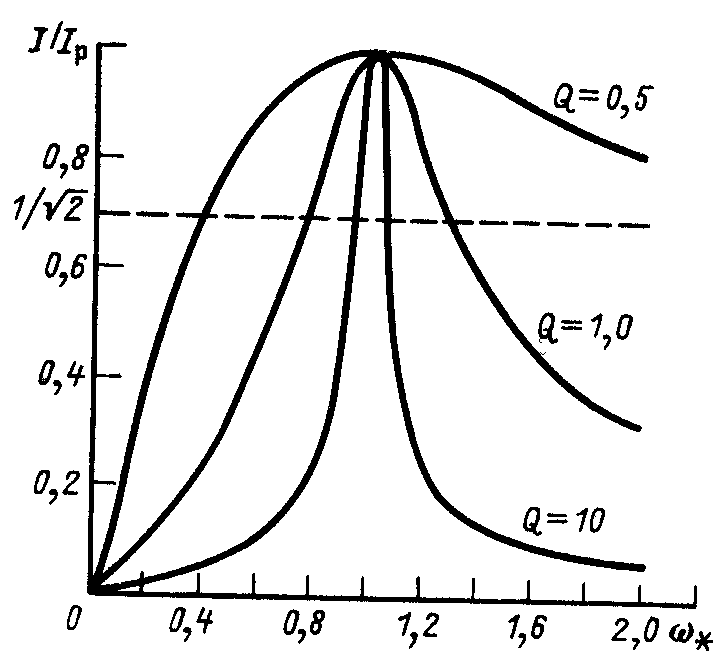
Рисунок 6

На рисунке 6 изображены графики резонансных кривых в относительных единицах. По оси ординат откладываем ток в долях от резонансного тока, а по оси абсцисс - частоту в долях от резонансной частоты. Чем меньше активное сопротивление резонансного контура при неизменных остальных параметрах схемы, т.е. чем больше добротность контура Q, тем более острой (пикообразной) становится форма кривой тока , где .

Для оценки избирательных свойств цепи вводят понятие полосы пропускания - полоса частот, на границах которой отношение составляет =0,707. На рисунке 6 проведена горизонтальная прямая на уровне = 0,707 , ее пересечение с резонансными кривыми определяет граничные частоты полосы пропускания контура и, следовательно, ширину полосы пропускания. Из рисунка видно, что чем выше добротность, тем уже полоса пропускания.