Приложение б Цепи однофазного синусоидального тока.

1. Математическое описание функции, синусоидально изменяющейся во времени.

Мгновение значение синусоидально изменяющейся величины выражается формулой:

, (1)

где _iначальная фаза (рисунок 1);

А_m – амплитудное значение или максимальное значение;

f =2T – угловая частота синусоидально изменяющейся величины;

f – частота переменного тока, Гц.

Рисунок 1

Для промышленной сети f=50Гц; 314 1/с.

Среднее значение синусоидально изменяющейся величины за период T= 2:

(2)

Для синусоиды A₀=0.

Среднеквадратическое (действующее) значение:

(3)

Для синусоиды A =A_m/ .

Синусоидальная функция a(t) может быть получена как проекция на вертикальную ось комплексной плоскости вектора A_m (рисунок 1), вращающегося в положительном направлении (против часовой стрелки) с угловой частотой 

Вектор имеет модуль, равный амплитуде ; он направлен в плоскости чертежа относительно горизонтальной оси под углом _i .

Вектор на комплексной плоскости выражается комплексной амплитудой синусоидально изменяющейся величины:

(4)

Вещественная (действительная) часть:

Re( ) = cos_i (5)

Мнимая часть:

Im( ) = sin_i 

Модуль комплексной амплитуды:

(7)

Аргумент комплексного числа:

(8)

2. Синусоидальный ток в пассивных элементах.

Пассивными линейными элементами электрической цепи синусоидального тока являются:

Резистивный элемент (резистор), обладающий сопротивлением R, индуктивный элемент (индукционная катушка) индуктивностью L и ёмкостной элемент (конденсатор без потерь) ёмкостью C.

Мгновенные значения напряжения U и тока i для пассивных элементов цепи синусоидального тока приведены в таблице 1 данного приложения. Там же даны комплексные изображения операторов комплексного сопротивления и комплексной проводимости ; приведены векторные и волновые диаграммы тока и напряжения на этих элементах.

Таблица 1. Мгновенные значения напряжения, тока для трех различных элементов цепи

Элемент	Уравнение для мгновенных значений i и u	Связь между и	Закон Ома: для амплитуд; в комплексной форме
Резистивный (резистор R)	, где R – коэффициент пропорциональности между напряжением u и i		1) где G=1/R; 2) где R – активное сопротивле- ние; G – активная проводи- мость
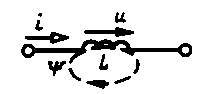
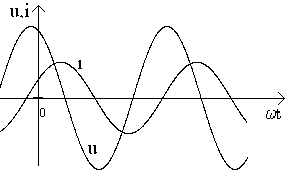
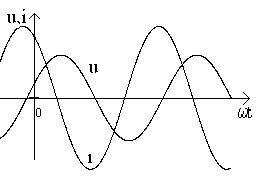
Индуктивный (индуктивность L)	, где L – коэффициент пропорциональности между потокосцеплением  и током i		где где - реактивное (индуктивное) сопротивление; - реактивная (индуктивная) проводимость, X = XL, B = BL
Ёмкостной (ёмкость C)	, где C - коэффициент пропорциональности между зарядом q и напряжением u		1) где ; где - реактивное (емкостное) проводимость; - реактивное (емкостное) сопротивление, X = -XС, B = -BС

Изображения и на комплексной плоскости	Векторная диаграмма ( ; )	Графики i(t) и u(t)

3. Законы Ома и Кирхгофа.

Для записи уравнений по Законам Кирхгофа (ЗК) надо выбрать положительное направление всех токов и обозначить их на схеме.

1 закон Кирхгофа (Закон Токов Кирхгофа или ЗТК) в применении к узлу электрической цепи для мгновенных и соответственно комплексных токов имеет вид:

(9)

При записи этих уравнений токи, направленные к узлу следует писать со знаком – плюс, а от узла со знаком – минус (или наоборот).

2 закон Кирхгофа (Закон Напряжений Кирхгофа или ЗНК) применяется к замкнутому контуру цепи и для мгновенных и соответственно комплексных падений напряжений и ЭДС имеет вид:

(10)

(11)

где - сумма падений напряжений на комплексных сопротивлениях отдельных участков.

Со знаком “ + ” берутся те слагаемые, для которых направление тока совпадает с направлением обхода; а со знаком “ – “ те слагаемые, для которых направление тока противоположно направлению обхода контура.

- алгебраическая сумма комплексных источников ЭДС.

4. Последовательное и параллельное соединение пассивных элементов.

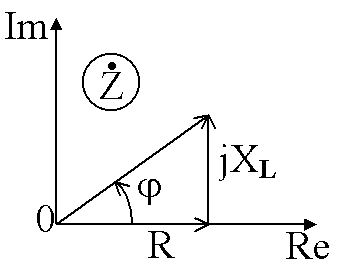
При последовательном соединении участков цепи (рисунок 2) комплексное эквивалентное сопротивление (рисунок 3) равно сумме комплексных сопротивлений участков:

Рисунок 2 Рисунок 3

(12)

При параллельном соединении ветвей цепи (рисунок 4) комплексная эквивалентная проводимость (рисунок 5) равна сумме комплексных проводимостей ветвей:

Рисунок 4 Рисунок 5

(13)

В частном случае двух параллельно соединённых сопротивлений и эквивалентное комплексное сопротивление:

(14)

Комплексные токи в любой из двух параллельных ветвей могут быть рассчитаны через комплексный ток в неразветвлённой части цепи и комплексного сопротивления ветвей по следующим формулам:

(15)

Синусоидальные ток и напряжение на выводах двухполюсников, состоящих из резистивного элемента и параллельно (последовательно) соединенного с ним индуктивного (емкостного) элемента приведены в таблице 2 данного приложения.

Таблица 2 Синусоидальные токи и напряжения на выводах двухполюсников

Схема	Уравнения для мгновенных значений i и u	Связь между и	Закон Ома в комплексной форме ( ; )
1	2	3	4
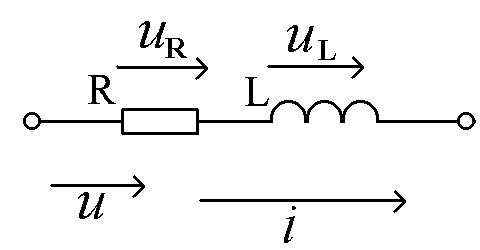
Последовательное соединение R и L	По второму закону Кирхгофа,
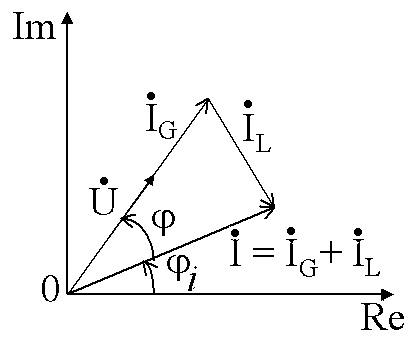
Параллельное соединение G и L	По первому закону Кирхгофа,

Изображения и на комплексной плоскости	Векторная диаграмма ( ; )	Графики i(t) и u(t)
5	6	7

Продолжение таблицы 2

1	2	3	4
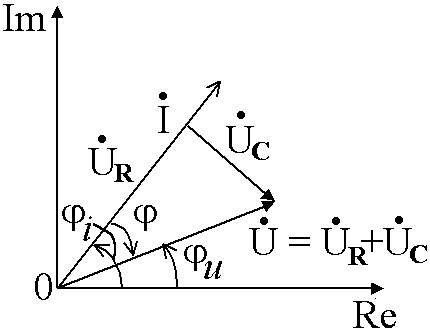
Последовательное соединение R и C	По второму закону Кирхгофа,
Параллельное соединение G и C	По первому закону Кирхгофа,

5	6	7