VI Исследование поведения функции и построение ее графика
Исследование поведения функции с помощью пределов
С
помощью пределов исследуются так
называемые асимптотические свойства
функции, то есть ее поведение либо при
,
либо при 
и 
.
Определение 6.1
Говорят,
что функция
=
имеет горизонтальную
асимптоту
,
если существует хотя бы один из пределов:
либо 
, либо 
.
Например,
функция 
имеет горизонтальную асимптоту
.
Определение 6.2
Говорят,
что функция
=
имеет вертикальную
асимптоту
, если имеет место хотя бы один из
пределов: 
,
,
,
.
Например,
функция 
имеет две вертикальные асимптоты 
и 
1,
так как
= 
= 
,
=
, 
= 
Определение 6.3
Прямая
называется наклонной асимптотой для
функции
=
при 
(при 
) , если выполнены два условия:
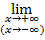
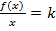б)
(
)
=
Например,
функция 
имеет наклонную асимптоту 
при
и при
,
так как
= 1 ,
= 3
Геометрически существование асимптоты у функции означает, что график функции становится близким к графику соответствующей прямой либо при (для горизонтальной или наклонной асимптоты), либо при (для вертикальной асимптоты). Это хорошо видно на рисунках 6.2 и 6.3.
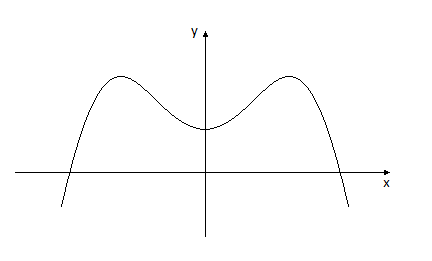
Рис. 6.1
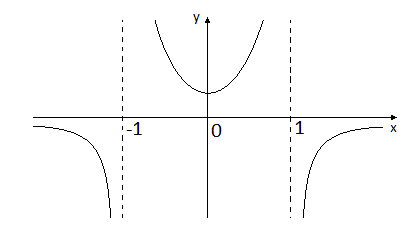
Рис.6.2
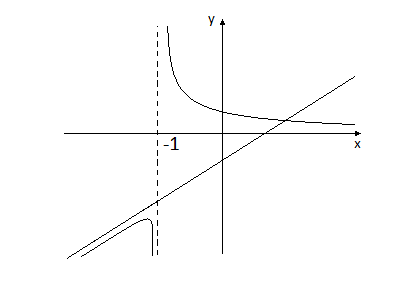
Рис.6.3
Исследование поведения функции с помощью производной
Как
мы знаем (теорема 5.2), с помощью производной
можно установить в области определения
функции интервалы , на которых функция
возрастает (
), убывает (
и найти точки экстремума (
.
Например,
функция
возрастает на интервале (
)
и убывает на интервале (
)
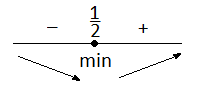
, так как ее производная 
меняет знак «+» на «-» лишь в точке
.
Производная
от функции
равна 
. На рисунке 6.1 указаны интервалы
монотонного возрастания (убывания)
этой функции и соответствующие точки
максимума и минимума.
Построение графика функции
Приведем некоторый алгоритм построения графика функции
Найти область определения функции и исследовать поведение функции на границе области определения.
Выяснить четность, нечетность функции и периодичность.
Определить нули функции и промежутки постоянства знака функции.
Определить точки экстремума и промежутки монотонности функции.
Найти уравнения асимптот, если они существуют.
Построить график функции.
Пример. Построить график функции
(
)
(
)
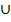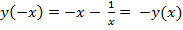- функция нечетная=
= 
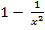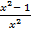
при |
| >1 ; 
при |
|< 1
, 
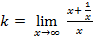= 1
=
= 0
– асимптота
)
=
Построим график этой функции
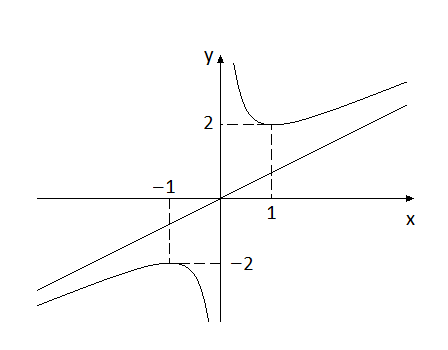
Пример 2
( ) ( ),
=
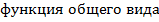
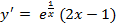
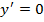
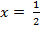
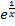асимптот
нет
= 
Построить графики функций
VII Наибольшее и наименьшее значение функций
Теорема
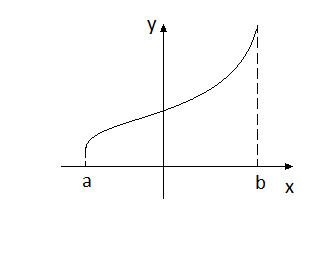
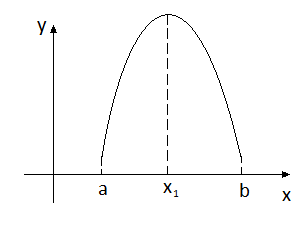
Непрерывная на отрезке функция достигает своего наибольшего и наименьшего значений либо в точках экстремума, либо на границе области задания.
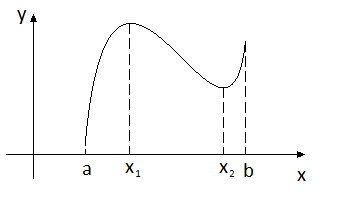
Поэтому можно предложить следующий алгоритм нахождения наибольшего и наименьшего значений.
Найти точки, в которых
.
Если найденные точки принадлежат
заданному отрезку [a,
b],
то подсчитать значения в этих точках.Найти значения на концах отрезка
и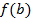 
.Выбрать из полученных значений наибольшее и наименьшее значения.
Пример
Найти наибольшее и наименьшее значения следующих функций
,
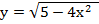=0,
,
,
= 
, 
=
1
= 
,
, 
= 
,
=
2